Numerično reševanje diferencialnih enačb - začetni problem

import numpy as np
from ipywidgets import interact
import matplotlib.pyplot as plt
%matplotlib inline
import sympy as sym
sym.init_printing()

Uvod

Zapis (ene) diferencialne enačbe

Predpostavimo, da je mogoče diferencialno enačbo prvega reda zapisati v eksplicitni obliki:

\[y'=f(t, y),\]

kjer je \(f(t, y)\) podana funkcija in velja \(y'=dy/dx\).

Dodatno je podan začetni pogoj:

\[y(t_0)=y_0.\]

Cilj reševanja diferencialne enačbe je izračunati funkcijo \(y(t)\), ki reši zgoraj definiran začetni problem. Ob določenih pogojih funkcije \(f(t, y)\) ima začetni problem enolično rešitev na intevalu, ki vsebuje \(t_0\).

Pri numeričnem reševanju vedno računamo tabelo funkcije \(y(t_i)\), ki reši dan začetni problem. Pri tem so vozlišča \(t_i\) običajno ekvidistantna:

\[t_0, t_0+h, t_0+2h,\dots\]

in \(h\) imenujemo (časovni) korak (integracije).

Tukaj si bomo pogledali nekatere numerične metode za reševanje diferencialnih enačb pri začetnem pogoju.

Eulerjeva metoda

Eksplicitna Eulerjeva metoda temelji na razvoju funkcije \(y\) v Taylorjevo vrsto:

\[y(t+h)=y(t)+y'(t, y(t))\,h + \mathcal{O}(h^2).\]

Naredimo napako metode \(\mathcal{O}(h^2)\), ker zanemarimo odvode drugega in višjih redov; sedaj lahko ob znani vrednosti \(y(t)\) in odvodu \(y'(t)=f(t,y)\) ocenimo vrednosti pri naslednjem časovnem koraku \(t+h\). Ko imamo enkrat znane vrednosti pri \(t+h\), ponovimo postopek!

Koraki Eulerjeve metode:

1. Postavimo \(i=0\), \(t_0\), \(y_0=y(t_0)\).

2. Izračun vrednosti funkcije pri \(t_{i+1}=t_i+h\): \(y_{i+1}= y_i + f(t_i, y_i)\,h.\)

3. \(i=i+1\) in nadaljevanje v koraku 2.

Diferencialno enačbo rešujemo na intervalu \([t_0,t_n]\) in velja \(h=(t_n-t_0)/n\). \(n\) je število integracijskih korakov (kolikokrat izvedemo korak 2 v zgornjem algoritmu).

Numerična rešitev začetnega problema:

\[y_0, y_1, y_2,\dots, y_{n}\]

pri vrednostih neodvisne spremenljivke:

\[t_0, t_1, t_2\, \dots \, t_n.\]

from IPython.display import YouTubeVideo
YouTubeVideo('cfZ8v0b-R8o', width=800, height=300)

Napaka Eulerjeve metode

Napaka Eulerjeve metode na vsakem koraku je reda \(\mathcal{O}(h^2)\).

Ker na intervalu od \(t_0\) do \(t_n\) tako napako naredimo \(n\)-krat, je kumulativna napaka \(n\,\mathcal{O}(h^2)=\frac{t_n-t_0}{h}\,\mathcal{O}(h^2)=\mathcal{O}(h)\).

Lokalno je napaka drugega reda, globalno pa je napaka prvega reda in ker je Eulerjeva metoda tako nenatančna jo redko uporabljamo v praksi!

Ocena napake

Točna rešitev \(y(t_n)\) pri velikosti koraka \(h\) je:

\[y(t_n)=y_{n,h}+E_h,\]

kjer je \(y_{n,h}\) numerični približek in \(E_h\) napaka metode. Ker je globalna napaka prvega reda, lahko napako zapišemo kot:

\[E_h=k\,h.\]

Podobno lahko za velikost koraka \(2h\) zapišemo:

\[y(t_n)=y_{n,2h}+E_{2h},\]

kjer je \(y_{n,2h}\) numerični približek in \(E_{2h}\) napaka metode:

\[E_{2h}=k\,2\,h.\]

Ob predpostavki, da je konstanta \(k\) pri koraku \(h\) in koraku \(2h\) enaka, lahko določimo oceno napake pri boljšem približku \(E_h\). Očitno velja:

\[y_{n,h}+k\,h=y_{n,2h}+2\,k\,h\]

nato določimo oceno napake:

\[E_h=k\,h=y_{n,h}-y_{n,2h}.\]

Komentar na implicitno Eulerjevo metodo

Pri eksplicitni Eulerjevi metodi računamo rešitev pri \(t_{i+1}\) iz izračunane vrednosti pri \(t_i\).

V kolikor bi nastopala neznana vrednost rešitve pri \(t_{i+1}\), to je \(y_{i+1}\), tudi na desni strani, bi govorili o implicitni Eulerjevi metodi (ali povratni Eulerjevi metodi):

\[y_{i+1}=y_i+f(t_{i+1}, y_{i+1})\,h.\]

Ker se iskana vrednost \(y_{i+1}\) nahaja na obeh straneh enačbe, moramo za določitev \(y_{i+1}\) rešiti (nelinearno) enačbo. Prednost implicitne Eulerjeve metode je, da je bolj stabilna (npr. v primeru togih sistemov, ki jih bomo spoznali pozneje) kakor eksplicitna oblika, vendar pa je numerično bolj zahtevna (zaradi računanja rešitve enačbe).

Numerična implementacija

Najprej uvozimo potrebne knjižnice:

import numpy as np
import matplotlib.pylab as plt
%matplotlib inline

Nato definirajmo Eulerjevo metodo:

def euler(f, t, y0, *args, **kwargs):
    """
    Eulerjeva metoda za reševanje sistema diferencialnih enačb: y' = f(t, y)
    
    :param f:  funkcija, ki vrne prvi odvod - f(t, y)
    :param t:  časovni vektor kjer računamo rešitev
    :param y0: začetna vrednosti
    :param args: dodatni argumenti funkcije f (brezimenski)
    :param kwargs: dodatni argumenti funkcije f (poimenovani)
    :return y: vrne np.array ``y`` vrednosti funkcije.
    """
    y = np.zeros_like(t)
    y[0] = y0        
    h = t[1]-t[0]
    for i in range(len(t)-1):
        y[i+1] = y[i] + f(t[i], y[i], *args, **kwargs) * h
    return y

Pripravimo funkcijo za oceno napake (v numeričnem smislu bi bilo bolje oceno napake vključiti v funkcijo euler, vendar jo zaradi jasnosti predstavimo ločeno):

def euler_napaka(f, t, y0, *args, **kwargs):
    """ Ocena napake Eulerjeve metode; argumenti so isti kakor za funkcijo `euler`
    """
    n = len(t)
    if n < 5:
        raise Exception('Vozlišč mora biti vsaj 5.')
    if n%2==0: # sodo vozlišč; odstrani eno točko in spremeni na liho (da je sodo odsekov)
        n = n - 1
    y_h = euler(f, t[:n], y0, *args, **kwargs)
    y_2h = euler(f, t[:n:2], y0, *args, **kwargs)
    E_h = y_h[-1] - y_2h[-1]
    return E_h

Numerični zgled

Kot primer rešimo diferencialno enačbo, ki opisuje padanje telesa, ki je izpostavljeno sili teže in zračnemu uporu:

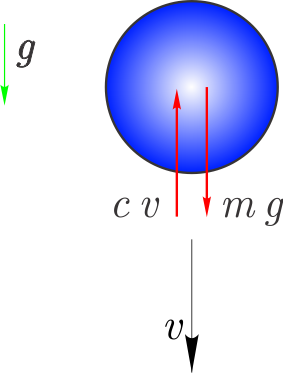
Glede na II. Newtonov zakon, lahko zapišemo diferencialno enačbo:

\[m\,g-c\,v=m\,v',\]

kjer je \(m\) masa, \(g\) gravitacijski pospešek, \(c\) koeficient zračnega upora in \(v\) hitrost. Diferencialno enačbo bi hoteli rešiti glede na začetni pogoj:

\[v(0)=0\,\textrm{m/s}.\]

Funkcija desne strani / prvega odvoda \(f(t,y)\) je:

\[f(t,y)=g-c\, \frac{y}{m}\]

in začetni pogoj:

\[y_0=0.\]

Definirajmo funkcijo desnih strani:

def f_zračni_upor(t, y, g=9.81, m=1., c=0.5):
    return g-c*y/m

Definirajmo začetni pogoj in časovni vektor, kjer nas zanima rezultat:

v0 = 0
t = np.linspace(0, 10, 11)
t

array([ 0.,  1.,  2.,  3.,  4.,  5.,  6.,  7.,  8.,  9., 10.])

Kličemo funkcijo euler za izračun vrednosti \(y\) (hitrost \(v\)):

y = euler(f_zračni_upor, t, y0=v0)
y

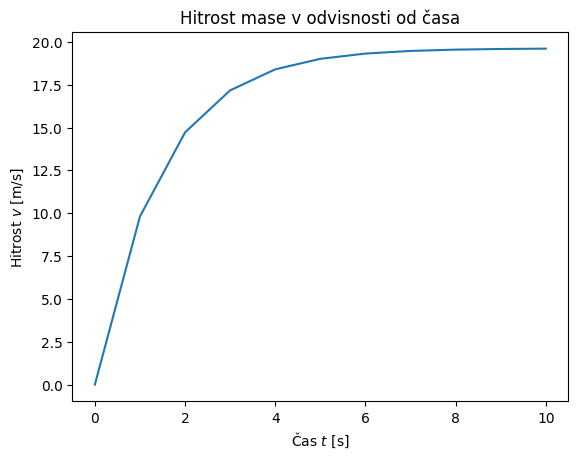
array([ 0.        ,  9.81      , 14.715     , 17.1675    , 18.39375   ,
       19.006875  , 19.3134375 , 19.46671875, 19.54335938, 19.58167969,
       19.60083984])

Prikažemo rezultat:

plt.plot(t, y)
plt.title('Hitrost mase v odvisnosti od časa')
plt.xlabel('Čas $t$ [s]')
plt.ylabel('Hitrost $v$ [m/s]')
plt.show()

Preverimo sedaj vpliv časovnega koraka:

for n in [11, 101, 1001]:
    t = np.linspace(0, 10, n)
    y = euler(f_zračni_upor, t, y0=v0, c=0.7)
    plt.plot(t, y, label=f'Časovni korak: {t[1]:1.0e}')
plt.title('Hitrost mase v odvisnosti od časa')
plt.xlabel('Čas $t$ [s]')
plt.ylabel('Hitrost $v$ [m/s]')
plt.legend()
plt.show()

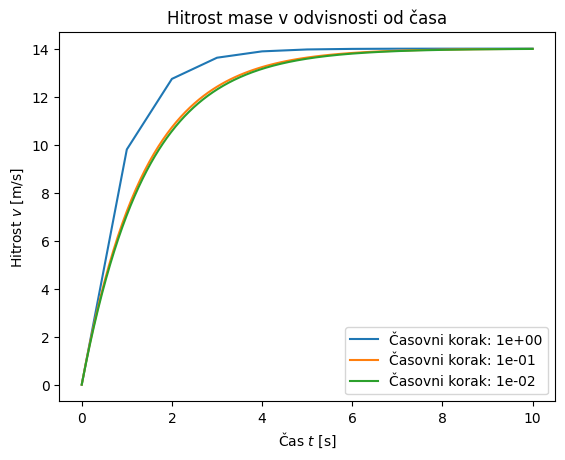
Opazimo, da se numerična napaka pri spremembi koraka iz 1 na 0,1 bistveno zmanjša!

Ocenimo še napako pri 100 in 1000 odsekih:

n=101
t = np.linspace(0, 10, n)
euler_napaka(f_zračni_upor, t, y0=v0)

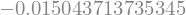
n=1001
t = np.linspace(0, 10, n)
euler_napaka(f_zračni_upor, t, y0=v0)

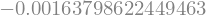
Ko smo korak zmanjšali na desetino, se je proporcionalno zmanjšala tudi napaka (prvi red napake).

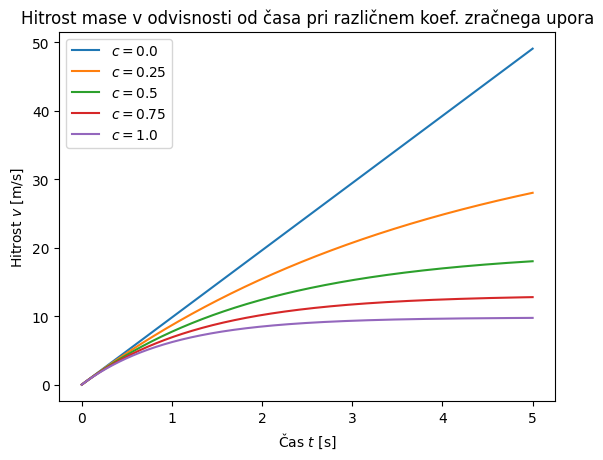
Poglejmo še primer, ko je zračni upor c argument funkcije euler in je prek **kwargs posredovan v funkcijo f_zračni_upor():

for c in np.linspace(0, 1, 5):
    t = np.linspace(0, 5, 1001)
    y = euler(f_zračni_upor, t, y0=v0, c=c)
    plt.plot(t, y, label=f'$c={c}$')
plt.title('Hitrost mase v odvisnosti od časa pri različnem koef. zračnega upora')
plt.xlabel('Čas $t$ [s]')
plt.ylabel('Hitrost $v$ [m/s]')
plt.legend()
plt.show()

Metoda Runge-Kutta drugega reda

Eulerjeva metoda je prvega reda (prvega reda je namreč globalna napaka \(\mathcal{O}(h)\)). Če bi želeli izpeljati metodo drugega reda napake, bi si morali pomagati z razvojem \(y(t+h)\) v Taylorjevo vrsto, kjer bomo zanemarili tretji in višje odvode:

\[y(t+h)=y(t)+y'(t)\,h + \frac{1}{2}y''(t)\,h^2+\mathcal{O}(h^3).\]

Lokalna napaka metode bo tako tretjega reda, globalna pa drugega reda.

Uporabimo zamenjavi \(y'(t)=f(t,y)\) in \(y''(t)=f'(t,y)\):

\[y(t+h)=y(t)+f(t,y)\,h + \frac{1}{2}f'(t,y)\,h^2+\mathcal{O}(h^3).\]

Ker je desna stran \(f(t,y)\) odvisna od neodvisne \(t\) in odvisne spremenljivke \(y\), moramo uporabiti implicitno odvajanje:

\[f'(t,y)=\frac{\partial f(t,y)}{\partial t}+\frac{\partial f(t,y)}{\partial y}\,\underbrace{\frac{\textrm{d} y}{\textrm{d} t}}_{y'=f(t,y)} =\frac{\partial f(t,y)}{\partial t}+\frac{\partial f(t,y)}{\partial y}\,{f(t, y)}.\]

Vstavimo v izraz za Taylorjevo vrsto:

\[y(t+h)_{\textrm{Taylor}}=y(t+h)=y(t)+f(t,y)\,h + \frac{1}{2}\,{\LARGE(} \frac{\partial f(t,y)}{\partial t}+\frac{\partial f(t,y)}{\partial y}\,{f(t, y)} {\LARGE)}\,h^2.\]

Kot je razvidno iz zgornjega izraza, potrebujemo dodatne odvode. To predstavlja določeno težavo, ki se ji lahko izognemo na različne načine; v nadaljevanju si bomo pogledali pristop Runge-Kutta. Ker bomo zgornji izraz pozneje še potrebovali, smo ga tukaj poimenovali \(y(t+h)_{\textrm{Taylor}}\).

Ideja pristopa Runge-Kutta

Zgornjo dilemo metoda Runge-Kutta (razvita leta 1901) rešuje z idejo, ki smo jo sicer že srečali pri Gaussovi integraciji: točnejšo rešitev poskuša najti z uteženo dodatno vrednostjo funkcije \(f\):

\[y(t+h)_{\textrm{Runge-Kutta}}=y(t)+c_0\,f\left(t,y\right)\,h +c_1 \underbrace{f{\large(}t+p\,h,y+q\,h\,f(t,y){\large)}}_{A}\,h.\]

kjer so \(c_0\), \(c_1\), \(p\) in \(q\) neznane konstante (načeloma od 0 do vključno 1). Če bi v zgornjem izrazu uporabili \(c_1=0\), bi izpeljali metodo prvega reda; z dodatno funkcijsko vrednostjo (\(A\)) pa se bo izkazalo, da bomo izpeljali metodo drugega reda.

Iskanje neznanih konstant \(c_0\), \(c_1\), \(p\), \(q\) nadaljujemo z zapisom \(A\) v obliki Taylorjeve vrste prvega reda:

\[f{\large(}t+p\,h,y+q\,h\,f(t,y){\large)}= \underbrace{ f{\large(}t,y{\large)}+ \frac{\partial f(t,y)}{\partial t}\,\left(p\,h\right)+ \frac{\partial f(t,y)}{\partial y}\,\left(q\,h\,f(t, y)\right) }_{B}.\]

Vstavimo sedaj izpeljani \(B\) nazaj v izraz za \(y(t+h)_{\textrm{Runge-Kutta}}\):

\[y(t+h)_{\textrm{Runge-Kutta}}=y(t)+c_0\,f\left(t,y\right)\,h +c_1 {\LARGE(} f{\large(}t,y{\large)}+ \frac{\partial f(t,y)}{\partial t}\,\left(p\,h\right)+ \frac{\partial f(t,y)}{\partial y}\,\left(q\,h\,f(t, y)\right) {\LARGE)} \,h.\]

Nadaljujemo z izpeljevanjem in enačbo preoblikujemo, da bo podobna zgoraj izpeljani s Taylorjevo vrsto \(y(t+h)_{\textrm{Taylor}}\):

\[y(t+h)_{\textrm{Runge-Kutta}}=y(t)+(c_0+c_1)\,f\left(t,y\right)\,h +\frac{1}{2} {\LARGE(} \frac{\partial f(t,y)}{\partial t}\,2\,c_1\,p+ 2\,c_1\,q\,\frac{\partial f(t,y)}{\partial y}\,f(t, y) {\LARGE)} \,h^2.\]

Primerjajmo sedaj z zgoraj izpeljanim izrazom:

\[y(t+h)_{\textrm{Taylor}}=y(t)+f(t,y)\,h + \frac{1}{2}\,{\LARGE(} \frac{\partial f(t,y)}{\partial t}+\frac{\partial f(t,y)}{\partial y}\,{f(t, y)} {\LARGE)}\,h^2.\]

Ugotovimo, da za enakost mora veljati:

\[c_0+c_1=1,\qquad 2\,c_1\,p=1,\qquad 2\,c_1\,q=1.\]

Imamo torej tri enačbe in štiri neznanke. Eno od konstant si tako lahko poljubno izberemo, ostale tri pa izračunamo. Če na primer izberemo \(c_0=0\), bi to imenovali spremenjena Eulerjeva metoda in bi ostali parametri bili: \(c_1=1\), \(p=q=1/2\). Izbira parametrov nima bistvenega vpliva na rešitev. Sicer pa velja omeniti, da tudi metodo Runge-Kutta drugega reda redko uporabljamo, saj obstajajo boljše metode.

Parametre \(c_0\), \(c_1\), \(p\) in \(q\) vstavimo v prvo enačbo tega poglavja. Ko je definiran začetni čas \(t_0\) in začetni pogoj \(y_0\), uporabimo metodo Runge-Kutta drugega reda:

\[y_{i+1} = y_i + f\left(t_i+\frac{1}{2}\,h, y_i+\frac{1}{2}\,h\,f(t_i,y_i)\right)\,h.\]

Metoda Runge-Kutta četrtega reda

Podobno kot smo izpeljali metodo Runge-Kutta drugea reda, se izpelje metodo Runge Kutta četrtega reda. Tudi pri metodi četrtega reda obstaja več različic in kot metoda Runge-Kutta četrtega reda razumemo naslednjo metodo:

\[y_{i+1}=y_i+\frac{1}{6}(k_0+2\,k_1+2\,k_2+k_3),\]

kjer so:

\[\begin{split}\begin{align} k_0&=h\,f(t_i,y_i)\\ k_1&=h\,f\left(t_i+\frac{h}{2},y_i+\frac{k_0}{2}\right)\\ k_2&=h\,f\left(t_i+\frac{h}{2},y_i+\frac{k_1}{2}\right)\\ k_3&=h\,f\left(t_i+h,y_i+k_2\right). \end{align} \end{split}\]

Koraki metode Runge-Kutta četrtega reda so:

1. Določitev \(i=0\) in \(t_0\), \(y_0=y(t_0)\),

2. Izračun koeficintov: \(k_0\), \(k_1\), \(k_2\), \(k_3\),

3. Izračun vrednosti rešitve diferencialne enačbe pri \(t_{i+1}=t_i+h\): \(\quad y_{i+1}=y_i+\frac{1}{6}(k_0+2\,k_1+2\,k_2+k_3),\)

4. \(i=i+1\) in nadaljevanje v koraku 2.

Napaka metode Runge-Kutta četrtega reda

Metodo Runge-Kutta četrtega reda imenujemo tako zato, ker ima lokalno napako petega reda \(\mathcal{O}(h^5)\), vendar pa to napako naredimo \(n\)-krat, zato je globalna napaka četrtega reda \(\mathcal{O}(h^4)\).

Ocena napake

Točen rezultat \(y(t_n)\) pri velikosti koraka \(h\) je:

\[y(t_n)=y_{n,h}+E_h,\]

kjer je \(y_{n,h}\) numerični približek rešitve in \(E_h\) napaka metode. Ker je globalna napaka četrtega reda, lahko napako zapišemo tako:

\[E_h=k\,h^4.\]

Podobno lahko za velikost koraka \(2h\) zapišemo:

\[y(t_n)=y_{n,2h}+E_{2h},\]

kjer je \(y_{n,2h}\) numerični približek rešitve in \(E_{2h}\) napaka metode:

\[E_{2h}=k\,(2\,h)^4=16\,k\,h^4.\]

Ob predpostavki, da je konstanta \(k\) pri koraku \(h\) in koraku \(2h\) enaka, lahko izračunamo oceno napake pri boljšem približku \(E_h\).

Najprej je res:

\[y_{n,h}+k\,h^4=y_{n,2h}+16\,k\,h^4,\]

sledi:

\[15\,k\,h^4=y_{n,h}-y_{n,2h}\]

in nato določimo oceno napake natančnejše rešitve:

\[E_h=\frac{y_{n,h}-y_{n,2h}}{15}.\]

Numerična implementacija

def runge_kutta_4(f, t, y0, *args, **kwargs):
    """
    Metoda Runge-Kutta 4. reda za reševanje diferencialne enačbe: y' = f(t, y)
    
    :param f: funkcija, ki jo kličemo s parametroma t in y in vrne 
              vrednost prvega odvoda
    :param t: ekvidistanten časovni vektor oz. neodvisna spremenljivka
    :param y0: začetna vrednost
    :param args: dodatni argumenti funkcije f (brezimenski)
    :param kwargs: dodatni argumenti funkcije f (poimenovani)
    :return y: funkcijske vrednosti.
    """
    def RK4(f, t, y, *args, **kwargs):
        k0 = h*f(t, y, *args, **kwargs)
        k1 = h*f(t + h/2.0, y + k0/2.0, *args, **kwargs)
        k2 = h*f(t + h/2.0, y + k1/2.0, *args, **kwargs)
        k3 = h*f(t + h, y + k2, *args, **kwargs)
        return (k0 + 2.0*k1 + 2.0*k2 + k3)/6.0
    
    y = np.zeros_like(t)
    y[0] = y0
    h = t[1]-t[0]

    for i, ti in enumerate(t[1:]):
        y[i+1] = y[i] + RK4(f, ti, y[i], *args, **kwargs)
        
    return y

Funkcija za oceno napake:

def runge_kutta_4_napaka(f, t, y0, *args, **kwargs):
    """ Ocena napake metode Runge Kutta 4; argumenti isti kakor za `runge_kutta_4`
    """
    n = len(t)
    if n < 5:
        raise Exception('Vozlišč mora biti vsaj 5.')
    if n%2==0: # sodo vozlišč; odstrani eno točko in spremeni na liho (da je sodo odsekov)
        n = n - 1
    y_h = runge_kutta_4(f, t[:n], y0, *args, **kwargs)
    y_2h = runge_kutta_4(f, t[:n:2], y0, *args, **kwargs)
    E_h = (y_h[-1] - y_2h[-1])/15
    return E_h

Numerični zgled

Poglejmo sedaj primer izračuna hitrosti padajoče mase:

def f_zračni_upor(t, y, g=9.81, m=1., c=0.5):
    return g-c*y/m

Podajmo začetni pogoj in časovni vektor, kjer nas zanima rezultat:

v0 = 0
t = np.linspace(0, 10, 11)
t

array([ 0.,  1.,  2.,  3.,  4.,  5.,  6.,  7.,  8.,  9., 10.])

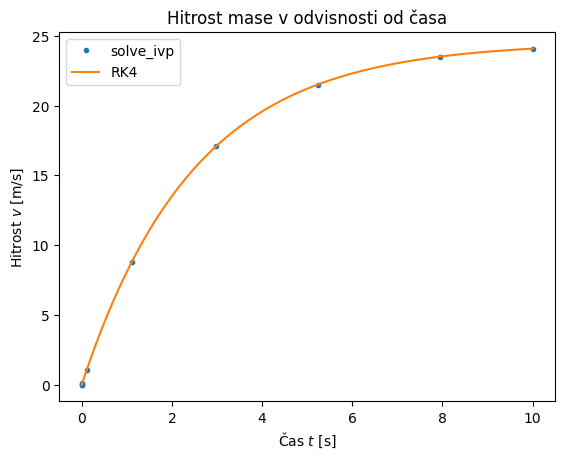
Za primerjavo izračunajmo rešitev s funkcijo euler ter runge_kutta_4:

y_euler = euler(f_zračni_upor, t, y0=v0, c=0.4)
y_rk4 = runge_kutta_4(f_zračni_upor, t, y0=v0, c=0.4)

Prikažemo rezultat:

plt.plot(t, y_euler, label='Euler')
plt.plot(t, y_rk4, label='RK4')
plt.title('Hitrost mase v odvisnosti od časa')
plt.xlabel('Čas $t$ [s]')
plt.ylabel('Hitrost $v$ [m/s]')
plt.legend()
plt.show()

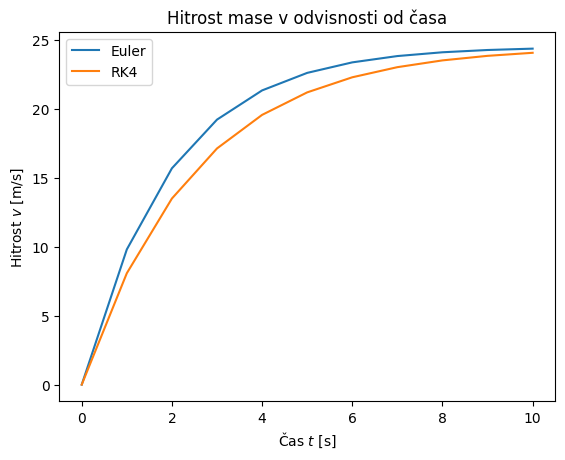
Poglejmo še numerično napako:

n=101
t = np.linspace(0, 10, n)
runge_kutta_4_napaka(f_zračni_upor, t, y0=v0, c=0.4)

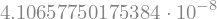
n=1001
t = np.linspace(0, 10, n)
runge_kutta_4_napaka(f_zračni_upor, t, y0=v0, c=0.4)

Pri zmanjšanju koraka na desetino, se je napaka zmanjšala za približno \(10^4\)-krat (kar ustreza pričakovanjem za metodo četrtega reda).

Uporaba scipy za reševanje navadnih diferencialnih enačb

Paket scipy ima implementiranih veliko numeričnih metod za reševanje začetnih problemov navadnih diferencialnih enačb. Tukaj si bomo ogledali funkcijo scipy.integrate.solve_ivp, ki je primerna za večino začetnih problemov.

scipy.integrate.solve_ivp

Sintaksa za uporabo (IVP - angl. Initial Value Problem):

scipy.integrate.solve_ivp(fun, t_span, y0, method='RK45', 
                          t_eval=None, dense_output=False, 
                          events=None, vectorized=False, **options)

Pojasnilo vseh argumentov je v dokumentaciji, tukaj bomo izpostavili nekatere:

• fun je desna stran (func(t, y...)),

• t_span terka (t0, tf), ki definira začetni t0 in končni čas tf,

• y0 seznam začetne(ih) vrednosti,

• method definira numerično metodo (privzeta je eksplicitna ‚RK45‘, za toge sisteme pa so boljše: ‚Radau‘, ‚BDF‘, ‚LSODA‘),

• t_eval uporabimo, če želimo rešitve ob določenih vrednosti neodvisne spremenljivke,

• dense_output ali se pripravi tudi zvezna rešitev, privzeto False,

• events za sledenje dogodkov, ki ustavijo reševanje začetnega problema.

Rezultat klicanja solve_ivp je objekt z atributi (izbrani):

• t vrednosti neodvisne spremenljivke pri katerih je izračunan rezultat,

• y rezultat,

• sol funkcija zvezne rešitve (samo v primeru dense_output=True)

• success je True, če je bila rešitev uspešno izračunana ali prekinjena zaradi dogodka (events).

Numerični zgled

Definirajmo začetni pogoj in časovni vektor, kjer nas zanima rezultat (prikažemo samo prvih deset elementov):

v0 = 0
t = np.linspace(0, 10, 101)
t[:10]

array([0. , 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9])

Argumente (npr.: c=0.4) v funkcijo fun vpeljemo prek lambda izraza (dokumentacija):

from scipy.integrate import solve_ivp
y_ivp = solve_ivp(lambda t,y: f_zračni_upor(t, y, c=0.4), t_span=(t[0], t[-1]), y0=[v0])

Zgoraj uporabljen lambda izraz lambda t, y: f_zračni_upor(t, y, c=0.4) je ekvivalenten:

def ime_funkcije(t, y):
    return f_zračni_upor(t, y, c=0.4)

Poglejmo rezultat:

y_ivp

  message: The solver successfully reached the end of the integration interval.
  success: True
   status: 0
        t: [ 0.000e+00  1.000e-04  1.100e-03  1.110e-02  1.111e-01
             1.111e+00  2.982e+00  5.236e+00  7.948e+00  1.000e+01]
        y: [[ 0.000e+00  9.810e-04  1.079e-02  1.086e-01  1.066e+00
              8.800e+00  1.708e+01  2.150e+01  2.350e+01  2.407e+01]]
      sol: None
 t_events: None
 y_events: None
     nfev: 56
     njev: 0
      nlu: 0

Ker je solve_ivp že pripravljen za sistem navadnih diferencialnih enačb prvega reda, je rezultat podan v dveh dimenzijah. Iskan rezultat je torej: y_ivp.y[0].

Za primerjavo še rezultat z lastno implementacijo Runge-Kutta 4. reda:

y_rk4 = runge_kutta_4(f_zračni_upor, t, y0=v0, c=0.4)

y_rk4[:10]

array([0.        , 0.96163898, 1.88557156, 2.77327623, 3.6261735 ,
       4.44562819, 5.23295161, 5.98940363, 6.71619474, 7.41448797])

Prikažemo rezultat:

plt.plot(y_ivp.t, y_ivp.y[0], '.', label='solve_ivp')
plt.plot(t, y_rk4, label='RK4')
plt.title('Hitrost mase v odvisnosti od časa')
plt.xlabel('Čas $t$ [s]')
plt.ylabel('Hitrost $v$ [m/s]')
plt.legend()
plt.show()

Sistem navadnih diferencialnih enačb

Zgoraj smo si pogledali reševanje začetnega problema ene navadne diferencialne enačbe; sedaj bomo reševanje posplošili na začetni problem za sistem \(m\) navadnih diferencialnih enačb prvega reda.

Takšen sistem zapišemo:

\[\mathbf{y}'=\mathbf{f}(t, \mathbf{y}),\]

kjer so podani dodatni (začetni) pogoji:

\[\mathbf{y}(t_0)=\mathbf{y}_0.\]

S \(t\) smo označili neodvisno spremenljivko (ni nujno, da je to vedno čas) in \(\mathbf{f}\) vektor desnih strani.

Računamo rešitev sistema \(m\) diferencialnih enačb \(\mathbf{y}'=\mathbf{f}(t, \mathbf{y})\) pri \(a=t_0, t_1,\dots,t_{n-1}=b\), to je \(m\) funkcijskih vrednosti na vsakem koraku \(y_k(t_i)\), \(k=0,1,\dots,m-1\) in \(i=0,1,\dots,n-1\). Lahko se dokaže, da lahko uporabimo vsako metodo, ki smo jo izpeljali za diferencialne enačbe prvega reda tudi za sistem navadnih diferencialnih enačb prvega reda, če zamenjamo skalarne veličine z ustreznimi vektorskimi.

Numerična implementacija

Metodi Euler in Runge-Kutta četrtega reda potrebujeta zgolj malenkostne popravke (y0 je numerično polje f vrne seznam vrednosti odvodov):

def euler_sistem(f, t, y0, *args, **kwargs):
    """
    Eulerjeva metoda za reševanje sistema navadnih diferencialnih enačb prvega reda : y' = f(t, y)
    
    :param f:  funkcija, ki jo kličemo s parametroma t in y in vrne seznam 
               funkcij desnih strani
    :param t:  ekvidistantni (časovni) vektor neodvisne spremenljivke
    :param y0: seznam začetnih vrednosti
    :param args: dodatni argumenti funkcije f (brezimenski)
    :param kwargs: dodatni argumenti funkcije f (poimenovani)
    :return y: vrne np.array ``y`` funkcijskih vrednosti.
    """
    y = np.zeros((t.shape[0], len(y0)))
    y[0] = np.copy(y0)
    h = t[1]-t[0]
    for i, ti in enumerate(t[:-1]):
        # tukaj je bistvo Eulerjeve metode
        y[i+1] = y[i]+f(ti, y[i], *args, **kwargs)*h
    return y

def runge_kutta_4_sistem(f, t, y0, *args, **kwargs):
    """
    Metoda Runge-Kutta 4. reda za reševanje sistema navadnih diferencialnih enačb prvega reda: y' = f(t, y)
    
    :param f:  funkcija, ki jo kličemo s parametroma t in y in vrne seznam 
               funkcij desnih strani
    :param t:  ekvidistantni (časovni) vektor neodvisne spremenljivke
    :param y0: seznam začetnih vrednosti
    :param args: dodatni argumenti funkcije f (brezimenski)
    :param kwargs: dodatni argumenti funkcije f (poimenovani)
    :return y: vrne np.array ``y`` funkcijskih vrednosti.
    """
    def RK4(g, t, y, *args, **kwargs):
        k0 = h*f(t, y, *args, **kwargs)
        k1 = h*f(t + h/2.0, y + k0/2.0, *args, **kwargs)
        k2 = h*f(t + h/2.0, y + k1/2.0, *args, **kwargs)
        k3 = h*f(t + h, y + k2, *args, **kwargs)
        return (k0 + 2.0*k1 + 2.0*k2 + k3)/6.0
    
    y = np.zeros((t.shape[0], len(y0)))
    y[0] = np.copy(y0)
    h = t[1]-t[0]

    for i, ti in enumerate(t[1:]):
        y[i+1] = y[i] + RK4(f, ti, y[i], *args, **kwargs)
        
    return y

Numerični zgled

Padanje mase nadgradimo v ravninsko gibanje; velikost sile upora zraka naj bo definirana kot: $\(|\mathbf{F}(\mathbf{v})|=c\,|\mathbf{v}|^2.\)$ Sila upora zraka deluje v nasprotno stran kot kaže vektor hitrosti.

Ob pomoči slike, definiramo silo v \(x\) smeri:

\[F_x=-c\,\left(v_x^2+v_y^2\right)\,\cos(\alpha)=-c\,\left(v_x^2+v_y^2\right)\,\frac{v_x}{\sqrt{v_x^2+v_y^2}}=-c\,v_x\,\sqrt{v_x^2+v_y^2}.\]

Podobno je sila v \(y\) smeri:

\[F_y=-c\,v_y\,\sqrt{v_x^2+v_y^2}.\]

Glede na drugi Newtonov zakon zapišemo sistem dveh (vezanih) diferencialnih enačb prvega reda:

\[F_x=m\,v_x',\]

\[m\,g+F_y=m\,v_y',\]

\(m\) je masa, \(g\) gravitacijski pospešek, \(c\) koeficient zračnega upora ter \(v_x\) in \(v_y\) hitrost v \(x\) oz \(y\) smeri. Diferencialno enačbo bi želeli rešiti glede na začetni pogoj:

\[v_x(0)=v_y(0)=5\,\textrm{m/s}.\]

Definirajmo seznam desnih strani:

def f_zračni_upor_sila(t, y,  g=9.81, m=1., c=0.5):
    vx, vy = y
    return np.array([-c*vx*np.sqrt(vx**2+vy**2)/m, g-c*vy*np.sqrt(vx**2+vy**2)/m])

Definirajmo začetni pogoj in časovni vektor, kjer nas zanima rezultat:

y0 = np.array([5., 5.])
t = np.linspace(0, 5, 101)
t[:5]

array([0.  , 0.05, 0.1 , 0.15, 0.2 ])

Za primerjavo izračunajmo rešitev s funkcijo runge_kutta_4 ter solve_ivp:

y_RK4 = runge_kutta_4_sistem(f_zračni_upor_sila, t=t, y0=y0)
y_ivp = solve_ivp(f_zračni_upor_sila, t_span=(t[0], t[-1]), y0=y0, t_eval=t)

Poglejmo rezultat:

y_ivp.y[:,:5]

array([[5.        , 4.23209907, 3.63858619, 3.16619484, 2.78087608],
       [5.        , 4.68459713, 4.48359747, 4.35932897, 4.28742151]])

y_RK4[:5].T

array([[5.        , 4.23211316, 3.6399137 , 3.16660748, 2.77780226],
       [5.        , 4.68462761, 4.48494405, 4.35999931, 4.28466858]])

Prikažemo rezultat:

plt.plot(t, y_ivp.y[0], label='$v_x$')
plt.plot(t, y_ivp.y[1], label='$v_y$')
plt.title('Hitrost mase (upor in sila) v odvisnosti od časa')
plt.xlabel('Čas $t$ [s]')
plt.ylabel('Hitrost $v$ [m/s]')
plt.legend()
plt.show()

Preoblikovanje diferencialne enačbe višjega reda v sistem diferencialnih enačb prvega reda

Pogledali si bomo, kako navadno diferencialno enačbo poljubnega reda \(n\):

\[y^{(n)}=f(t, y, y', y'',\dots,y^{(n-1)}),\]

pri začetnih pogojih:

\[y(t_0)=k_0,\quad y'(t_0)=k_1,\quad\dots\quad y^{(n-1)}(t_0)=k_{n-1}\]

preoblikujemo v sistem diferencialnih enačb prvega reda.

Najprej namesto odvodov vpeljemo nove spremenljivke:

\[y_i=y^{(i)}, \qquad i=0,1,\dots,n-1.\]

Diferencialna enačba \(n\)-tega reda zapisana z novimi spremenljivkami je:

\[y_{n-1}'=f(t, y_0, y_1, y_2,\dots,y_{n-1}).\]

Nove funkcije odvajamo po neodvisni spremenljivki:

\[y_i'=y^{(i+1)}=y_{i+1}, \qquad i=0,1,\dots,n-2\]

in $\(y_{n-1}'=f(t, y_0, y_1, y_2,\dots,y_{n-1}).\)$

Dobili smo sistem navadnih diferencialnih enačb prvega reda:

\[\begin{split} \begin{array}{rcl} y_0'&=&y_1\\ y_1'&=&y_2\\ &\dots\\ y_{n-1}'&=&f(t, y_0, y_1, y_2,\dots,y_{n-1})\\ \end{array} \end{split}\]

pri začetenih pogojih:

\[y_0(t_0)=k_0,\quad y_1(t_0)=k_1,\quad\dots\quad y_{(n-1)}(t_0)=k_{n-1}.\]

Numerični zgled

Vrnemo se k padajoči masi:

Vendar tokrat drugi Newtonov zakon zapišimo glede na pomik (diferencialna enačba drugega reda):

\[F_x=m\,x'',\]

\[m\,g+F_y=m\,y'',\]

\(m\) je masa, \(g\) gravitacijski pospešek, \(c\) koeficient zračnega upora ter \(x''\) in \(y''\) pospešek v izbranem koordinatnem sistemu. Začetni pogoji:

\[x(0)=y(0)=0\,\textrm{m}\qquad\textrm{in}\qquad x'(0)= y'(0)=5\,\textrm{m/s}.\]

Imamo sistem dveh diferencialnih enačb drugega reda. Z uvedbo novih spremenljivk \(y_i\):

\[y_0= x,\quad y_1= x',\quad y_2= y,\quad y_3= y'.\]

Pripravimo sistem diferencialnih enačb prvega reda:

\[\begin{split} \begin{array}{rcl} y_0'&=&y_1\\ y_1'&=&F_x/m\\ y_2'&=&y_3\\ y_3'&=&g+F_y/m \end{array} \end{split}\]

Definirajmo Pythonovo funkcijo desnih strani / prvih odvodov:

def f_zračni_upor_vezana(t, y, g=9.81, m=1., c=0.5):
    x, vx, y, vy = y
    return np.array([vx, -c*vx*np.sqrt(vx**2+vy**2)/m, vy, g-c*vy*np.sqrt(vx**2+vy**2)/m])

Definirajmo začetni pogoj in časovni vektor, kjer nas zanima rezultat:

y0 = np.array([0., 5., 0., 5.])
t = np.linspace(0, 5, 101)
t[:5]

array([0.  , 0.05, 0.1 , 0.15, 0.2 ])

Izračunamo rešitev:

y_ivp = solve_ivp(f_zračni_upor_vezana, t_span=(t[0], t[-1]), y0=y0, t_eval=t)

Poglejmo rezultat (\([x, x', y, y']\)):

y_ivp.y[:,:5]

array([[0.        , 0.22992477, 0.42611996, 0.59587483, 0.74424286],
       [5.        , 4.23183658, 3.64002431, 3.16703014, 2.77775353],
       [0.        , 0.24153615, 0.47038377, 0.69124852, 0.9072755 ],
       [5.        , 4.68435696, 4.48497294, 4.36034218, 4.28444004]])

Prikažemo rezultate; najprej hitrost, nato lego (\(y\) koordinata je pozitivna navzdol)!

plt.plot(t, y_ivp.y[1], label='$v_x$')
plt.plot(t, y_ivp.y[3], label='$v_y$')
plt.title('Hitrost mase v odvisnosti od časa')
plt.xlabel('Čas $t$ [s]')
plt.ylabel('Hitrost [m/s]')
plt.legend()
plt.show()

plt.scatter(y_ivp.y[0], y_ivp.y[2], marker='.')
plt.xlabel('$x$ [m]')
plt.ylabel('$y$ [m]')
plt.title('Lega mase')
plt.show()

Stabilnost reševanja diferencialnih enačb*

Numerično reševane diferencialnih enačb je izpostavljeno napaki metode in zaokrožitveni napaki. Te napake so pri različnih numeričnih metodah različne.

Reševanje diferencialne enačbe je stabilno, če majhna sprememba začetnega pogoja vodi v majhno spremembo izračunane rešitve; sicer govorimo o nestabilnosti reševanja.

Stabilnost je odvisna od diferencialne enačbe, od uporabljene numerične metode in od koraka integracije \(h\).

Primer preprostega nihala

Poglejmo si najprej primer reševanja diferencialne enačbe preprostega nihala.

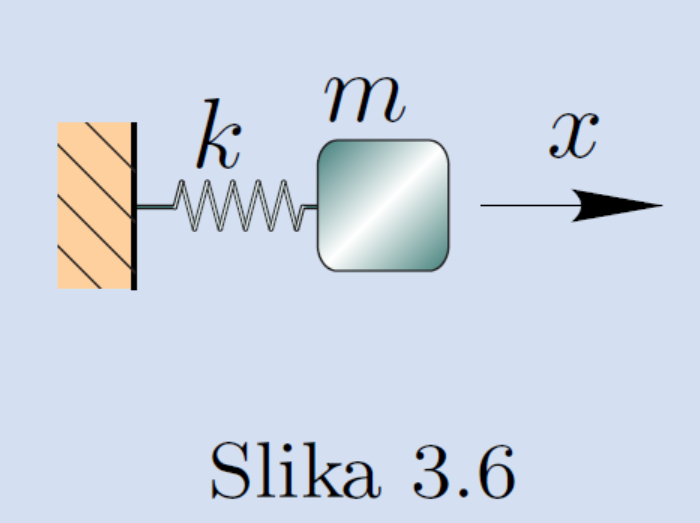
Slika (vir: Slavič, Dinamika, mehanska nihanja in mehanika tekočin, 2017) prikazuje dinamski sistem (masa \(m\), togost \(k\)), katerega diferencialna enačba je

\[m\, x'' + k\,x=0.\]

Tako diferencialno enačbo preoblikujemo v standardno obliko lastnega nihanja:

\[x'' + \omega_0^2\,x=0,\]

kjer je lastna krožna frekvenca:

\[\omega_0=\sqrt{\frac{k}{m}}\]

in pričakujemo odziv oblike:

\[x(t)=A\,\cos(\omega_0\,t)+B\,\sin(\omega_0\,t).\]

Če so začetni pogoji:

\[x(0\,\textrm{s})=x_0\qquad\textrm{in}\qquad x'(0\,\textrm{s})=0\,\textrm{m/s},\]

je rešitev začetnega problema:

\[x(t)=x_0\,\cos(\omega_0\,t).\]

Numerični zgled

Najprej definirajmo vektor začetnih pogojev in funkcijo desnih strani / prvih odvodov (diferencialno enačbo drugega reda pretvorimo v sistem diferencialnih enačb prvega reda \(\mathbf{y}'=\mathbf{f}(t, \mathbf{y})\)), kjer velja \(y_0=x, y_1=x'\):

def f_nihalo(t, y, omega0=2*np.pi):
    """
    Funkcija desnih strani za nihalo z eno prostostno stopnjo
    
    :param t: čas
    :param y: seznam začetnih vrednosti
    :param omega: lastna krožna frekvenca
    :return y': seznam vrednosti odvodov
    """
    return np.array([y[1], -omega0**2*y[0]])

Definirajmo podatke in analitično rešitev:

x0 = 1.
omega0 = 2*np.pi
x_zacetni_pogoji = np.array([x0, 0.])
t1 = 4.
cas = np.linspace(0, t1, 500)
pomik = x0*np.cos(omega0*cas) # analitična rešitev
hitrost = -x0*omega0*np.sin(omega0*cas) # analitična rešitev

Rešitev s pomočjo metod Euler in Runge-Kutta četrtega reda:

t_Eu = np.linspace(0, t1, 101)
t_RK4 = t_Eu
dt = t_Eu[1]

x_Eu = euler_sistem(f_nihalo, t_Eu, x_zacetni_pogoji)
x_RK4 = solve_ivp(f_nihalo, t_span=(t_RK4[0], t_RK4[-1]), y0=x_zacetni_pogoji, t_eval=t_RK4).y

Prikažimo rezultate:

plt.plot(cas, pomik, label='Analitična rešitev')
plt.plot(t_Eu, x_Eu[:,0], '.', label='Euler')
plt.plot(t_RK4, x_RK4[0], '.', label='Runge-Kutta 4')
plt.legend()
plt.title('Stabilnost različnih metod')
plt.ylabel('Pomik [m]')
plt.xlabel('Čas [s]')
plt.show()

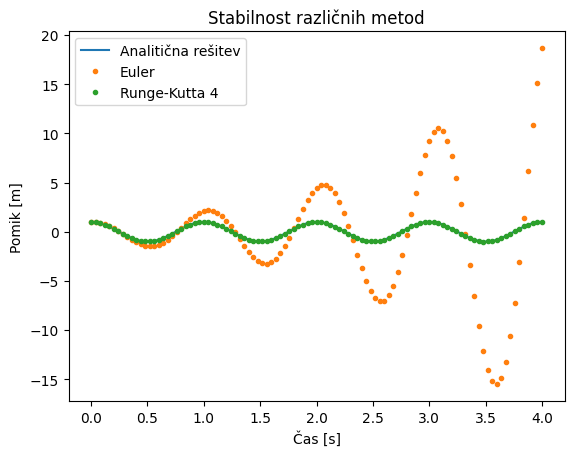
Opazimo, da je Eulerjeva metoda nestabilna in če bi povečali korak, bi postala nestabilna tudi metoda Runge-Kutta četrtega reda.

Zakaj je Eulerjeva metoda tako nestabilna?

x_Eu[:10,0]

array([ 1.        ,  1.        ,  0.93683453,  0.8105036 ,  0.62499707,
        0.3882947 ,  0.1121141 , -0.18859332, -0.49638247, -0.79225904])

Spomnimo se Eulerjeve metode:

\[x(t+h)=x(t)+x'(t)\,h,\]

ki nam pove, da pomik \(x(t+h)\) določimo glede na lego \(x(t)\) in hitrost \(x'(t)\). Začetni pogoji izhajajo iz skrajnega odmika \(x(t=0)=1\) in takrat je hitrost \(x'(t=0)=0\), kar pomeni, da bo \(x(t+h)=1\). Že v prvem koraku torej naredimo razmeroma veliko napako. Vendar zakaj potem začne vrednost alternirajoče naraščati?

Spomnimo se, da je analitična rešitev \(x(t)=x_0\,\cos(\omega_0\,t)\) in je torej \(x'(t)=-\omega_0\,x_0\,\sin(\omega_0\,t)\).

Vstavimo pripravljena izraza v Eulerjevo metodo in uredimo:

\[x(t+h)=x(t)+x'(t)\,h=x_0\,\left(\cos(\omega_0\,t)-\omega_0\,h\,\sin(\omega_0\,t)\right).\]

Predpostavimo, da gledamo stanje ob takem času \(t=\pi/(2\omega_0)\), ko velja \(\cos(\omega_0\,t)=0\) in \(\sin(\omega_0\,t)=1\):

\[x(t+h)=x_0\,\underbrace{\left(-\omega_0\,h\right)}_{A}.\]

V kolikor bo absolutna vrednost izraza \(A\) večja kot 1, bo pri času \(t+h\) vrednost večja kot v predhodnem koraku in v sledečem verjetno spet. Sledi, da lahko pride do nestabilnosti. Da se je izognemo, mora veljati:

\[|A|<1\qquad\rightarrow\qquad h<\frac{1}{\omega_0}.\]

Opomba: v nekaterih knjigah boste videli tudi vrednost \(h<2/\omega_0\); enoliče meje za vse diferencialne enačbe ni mogoče definirati; v splošnem pa velja, da je korak definiran relativno glede na najkrajšo periodo \(T\) v diferencialni enačbi (npr.: \(h<2/\omega_0\) je v bistvu enako \(h<2/(2\pi/T)\) oziroma \(h<T/\pi\)). Perioda \(T\) je definirana glede na najvišjo lastno frekvenco sistema \(T=1/f_{\textrm{max}}\), ki jo izračunamo iz lastne vrednosti sistema.

Nekaj vprašanj za razmislek!

1. Na sliki (vir: Numerical Methods in Engineering With Python 3, 3rd Ed, Jaan Kiusalaas) je prikazan izstrelek mase \(m\), ki ga izstrelimo s hitrosjo \(v_0\) pod kotom \(\alpha\). Če je sila upora zraka: \(F=c\,v^{3/2}\), potem sta gibalni enačbi:

\[\ddot x(t)=-F\,\cos(\alpha)/m\qquad\ddot y(t)=-F\,\sin(\alpha)/m-g.\]

Opomba: \(v=\sqrt{\dot x^2+\dot y^2}.\) Ustrezne parametre si izmislite. Sistem dveh diferencialnih enačb drugega reda zapišite v sistem diferencialnih enačb prvega reda. 2. Določite vektor začetnih pogojev, ki smo ga zgoraj označili z \(\mathbf{y}\). 3. Določite funkcijo desnih strani, c naj bo parameter. 4. Definirajte začetne pogoje in rešite nalogo s poljubnimi podatki. 5. Prikažite \((x, y)\) lego masne točke, spreminjajte koeficient upora \(c\). 6. Prikažite hitrost v odvisnosti od časa. Določite minimum hitrosti in čas, pri katerem nastane.

Primer Van der Polovega nihala

Namen tega primera je pokazati, kako lahko izbira integratorja vpliva na hitrost reševanja problema! Van der Polovo nihalo je opisano tukaj.

Definirajmo seznam odvodov:

def f_van_der_pol(t, y, mu=1000):
    """
    Funkcija desnih strani za Van der Pol nihalo
    
    :param t: čas
    :param y: seznam začetnih vrednosti
    :param mu: parameter dušenja in nelinearnosti
    :return y': seznam vrednosti odvodov
    """
    return np.array([y[1], mu*(1-y[0]**2)*y[1]-y[0]])

x_zacetni_pogoji = np.array([1.5, 0.])
dt = 0.1
t1 = 3000

Rešitev po metodi RK45 (gre za eksplicitno shemo, ki ni primerna za toge sisteme diferencialnih enačb; reševanje je zelo počasno, zato rešitev računamo samo do t1/100):

vp_RK45 = solve_ivp(f_van_der_pol, t_span=(0., t1/100), y0=x_zacetni_pogoji, method='RK45')

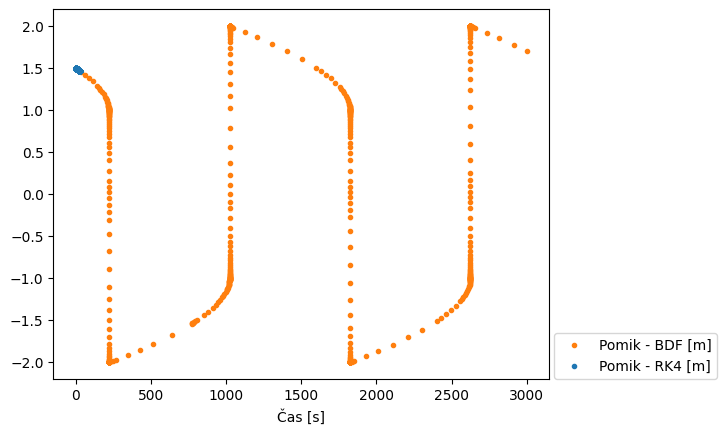
Implicitna shema BDF (angl. Backward Differentiation Formulas) se tukaj izkaže kot bistveno bolj primerna. Zaradi stabilnosti, so koraki lahko bistveno večji in zato je reševanje bistveno hitrejše:

vp_BDF = solve_ivp(f_van_der_pol, t_span=(0., t1), y0=x_zacetni_pogoji, method='BDF')

plt.plot(vp_BDF.t, vp_BDF.y[0], 'C1.', label='Pomik - BDF [m]')
plt.plot(vp_RK45.t, vp_RK45.y[0], 'C0.', label='Pomik - RK4 [m]')
plt.xlabel('Čas [s]')
plt.legend(loc=(1.01, 0));

Simbolno reševanje diferencialne enačbe drugega reda

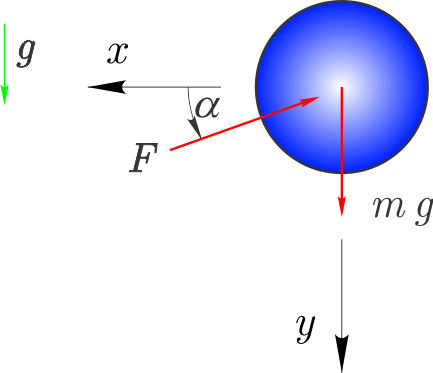
Pogledali si bomo primer, prikazan na sliki, kjer je masa \(m\) na klancu naklona \(\alpha\). Koeficient trenja je \(\mu\), težnostni pospešek pa \(g\). Začetna hitrost je \(\dot y(0\,\textrm{s})=v_0\), pomik \(y(0\,\textrm{s})=0\,\textrm{m}\). 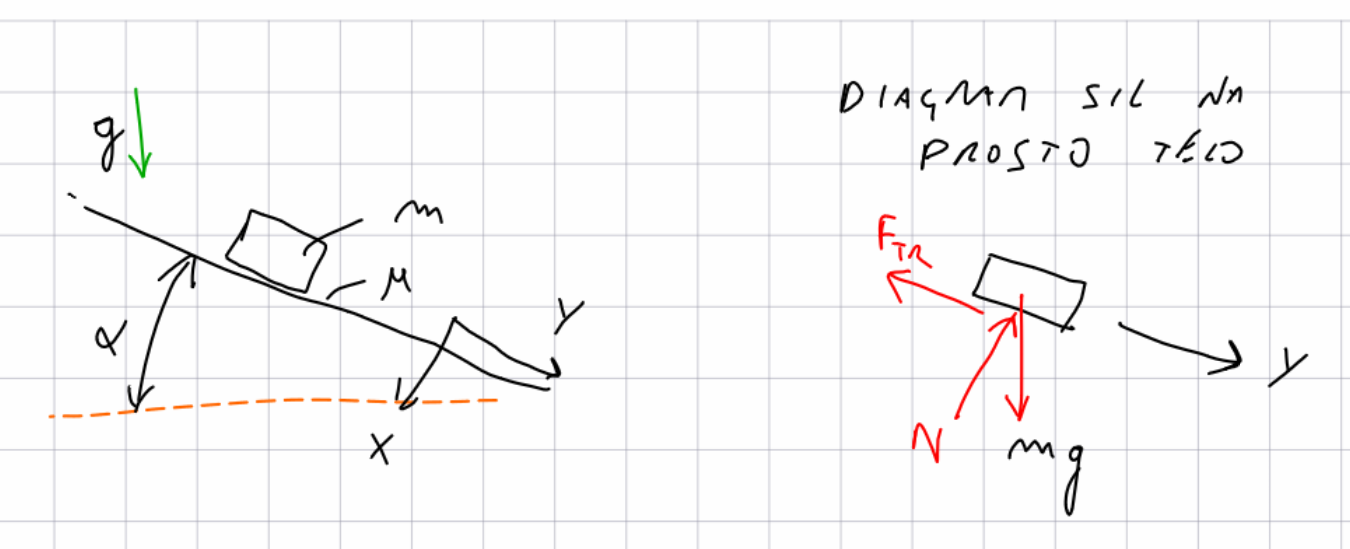Gibalna enačba (samo za smer \(y\)) je definirana glede na II. Newtonov zakon (glejte diagram sil na prosto telo).

Izpeljava gibalne enačbe

y = sym.Function('y')
m, mu, g, alpha, t, v0 = sym.symbols('m, mu, g, alpha, t, v0')
eq = sym.Eq(m*y(t).diff(t,2),  m*g*sym.sin(alpha)-m*g*sym.cos(alpha)*mu)
eq

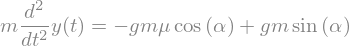
Rešitev enačbe je:

dsol = sym.dsolve(eq, y(t))
dsol

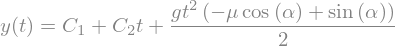
Da določimo \(C_1\) in \(C_2\), vstavimo \(t=0\,\textrm{s}\):

dsol.args[1].subs(t, 0)

Nato odvajamo po času in ponovno vstavimo \(t=0\,\textrm{s}\):

dsol.args[1].diff(t).subs(t, 0)

Glede na začetne pogoje smo torej določili konstante:

zacetni_pogoji = {'C1': 0, 'C2': v0}

Sledi rešitev:

resitev = dsol.args[1].subs(zacetni_pogoji)
resitev

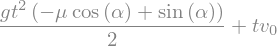
Pripravimo si funkciji za numerični klic:

podatki = {mu: 0.3, alpha: 15*np.pi/180, v0: 1., g: 9.81} #tukaj uporabimo np.pi, da imamo numerično vrednost

pomik = sym.lambdify(t, resitev.subs(podatki), 'numpy')
hitrost = sym.lambdify(t, resitev.diff(t).subs(podatki), 'numpy')

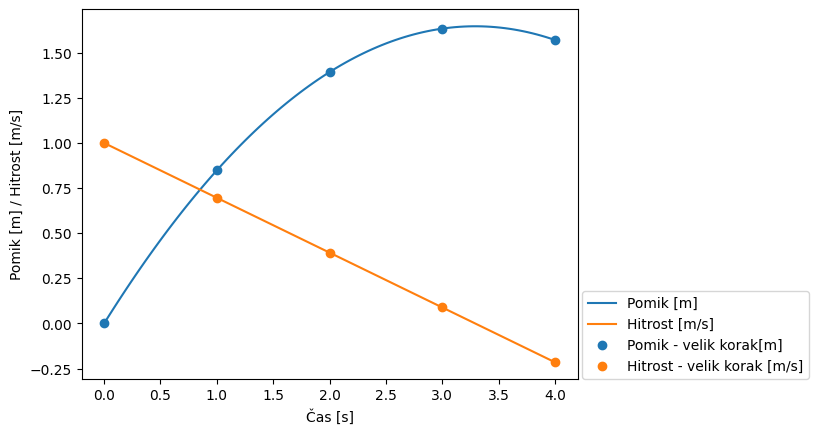
print('Pomik pri 0s: {:g}m'.format(pomik(0)))
print('Hitrost pri 0s: {:g}m/s'.format(hitrost(0)))

Pomik pri 0s: 0m
Hitrost pri 0s: 1m/s

Pripravimo prikaz:

cas = np.linspace(0, 4, 100)
cas2 = np.linspace(0, 4, 5)

def slika():
    plt.plot(cas, pomik(cas), 'C0', label='Pomik [m]')
    plt.plot(cas, hitrost(cas), 'C1', label='Hitrost [m/s]')
    plt.plot(cas2, pomik(cas2), 'C0o', label='Pomik - velik korak[m]')
    plt.plot(cas2, hitrost(cas2), 'C1o', label='Hitrost - velik korak [m/s]')
    plt.xlabel('Čas [s]')
    plt.ylabel('Pomik [m] / Hitrost [m/s]')
    plt.legend(loc=(1.01, 0));
    plt.show()

slika()

Simbolno preoblikovanje diferencialne enačbe v sistem diferencialnih enačb prvega reda

Spomnimo se izvorne diferencialne enačbe:

eq

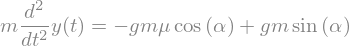
Definirajmo nove spremenljivke in pripravimo funkcijo \(f\):

y0 = sym.Function('y0')
y1 = sym.Function('y1')
f = sym.simplify(eq.args[1]/m)
f

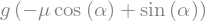
Povežimo sedaj nove spremenljivke.

\(d y_0/dt\) naj bo enako \(y_1\):

eq1 = sym.Eq(y0(t).diff(t), y1(t))
eq1

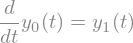
Odvod \(d y_1/dt\) (v bistvu je to \(y''\)) naj bo enak funkciji \(f\):

eq2 = sym.Eq(y1(t).diff(t), f)
eq2

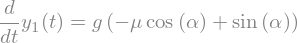
Zgornje izraze zapišemo v vektorski obliki: $\(\mathbf{y}'=\mathbf{f}(t, \mathbf{y}).\)$

y_odvod = [y0(t).diff(t), y1(t).diff(t)]
y_odvod

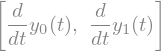
f_vec = [y1(t), f]
f_vec

Spomnimo se sedaj f_vec:

f_vec

Če rešujemo numerično, potem funkcijo \(\mathbf{f}(t, \mathbf{y})\) zapišemo:

pospesek = float((eq.args[1]/m).simplify().subs(podatki))
pospesek #raziščite zakaj smo tukaj tako definirali! namig: type(pospesek)

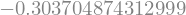
def F_klada(t, y):
    return np.array([y[1], pospesek],dtype=float)

Preverimo funkcijo pri začetnem času \(t=0\,\)s in pri začetnih pogojih \([y_0, y_1]=[0, v_0]\):

y_zacetni_pogoji = np.array([0, podatki[v0]])
y_zacetni_pogoji

array([0., 1.])

F_klada(0., y_zacetni_pogoji)

array([ 1.        , -0.30370487])

Uporabimo sedaj Eulerjevo metodo:

#%%timeit
x_Eu = np.linspace(0, 4, 5)
y_Eu = euler_sistem(F_klada, x_Eu, np.array([0, 1.]))
y_Eu

array([[ 0.        ,  1.        ],
       [ 1.        ,  0.69629513],
       [ 1.69629513,  0.39259025],
       [ 2.08888538,  0.08888538],
       [ 2.17777075, -0.2148195 ]])

Prikažemo in primerjamo z analitično rešitvijo:

def narisi_euler(n=5):
    x_Eu = np.linspace(0, 4, n)
    y_Eu = euler_sistem(F_klada, x_Eu, np.array([0, 1.]))
    plt.title('Eulerjeva metoda s korakom $h={:g}$'.format(x_Eu[1]-x_Eu[0]))
    plt.plot(cas, pomik(cas), 'C0', label='Pomik - analitično [m]')
    plt.plot(cas, hitrost(cas), 'C1', label='Hitrost - analitično [m/s]')
    plt.plot(x_Eu, y_Eu[:, 0], 'C0.', label='Pomik - Euler [m]')
    plt.plot(x_Eu, y_Eu[:, 1], 'C1.', label='Hitrost - Euler [m/s]')
    plt.xlabel('Čas [s]')
    plt.ylabel('Pomik [m] / Hitrost [m/s]')
    plt.ylim(-0.5, 2.5)
    plt.legend(loc=(1.01, 0))
    plt.show();

interact(narisi_euler, n=(3, 10, 1));