Reševanje enačb#
Uvod#
Za uvod si oglejmo spodnji video:
from IPython.display import YouTubeVideo
YouTubeVideo('17d55KE8SIU', width=800, height=300)
V okviru reševanja enačb obravnavamo poljubno enačbo, ki je odvisna od spremenljivke \(x\) in iščemo rešitev:
Rešitvam enačbe rečemo tudi koreni (angl. roots). Koren enačbe \(f(x)=0\) je hkrati tudi ničla funkcije \(y=f(x)\).
Funkcija \(y=f(x)\) ima lahko ničle stopnje:
ničla prve stopnje: funkcija seka abscisno os pod neničelnim kotom,
ničle sode stopnje: funkcija se dotika abscisne osi, vendar je ne seka,
ničle lihe stopnje: funkcija seka abscisno os, pri ničli stopnje 3 in več imamo prevoj (tangenta je vzporedna z abscisno osjo).
Tukaj je pomembno izpostaviti, da iščemo rešitev poljubne enačbe \(f(x)=0\). Če za linearne, kvadratne ali kubične enačbe, lahko določimo analitične rešitve; za večino nelinearnih enačb analitične rešitve ne moremo določiti. Iz tega razloga so numerični pristopi toliko bolj pomembni.
Omejitve funkcije \(f(x)\)#
Za funkcijo \(y=f(x)\) zahtevamo, da je na zaprtem intervalu \([x_0, x_1]\) zvezna. Pri računanju ničel, se bomo omejili samo na ničle prve stopnje.
Zgled#
Poljubno funkcijo \(y=f(x)\) lahko definiramo s Pythonovo funkcijo; za zgled tukaj definirajmo polinom:
def f(x):
return x**3 - 10*x**2 + 5
Ker pa gre za polinom \(x^3-10x^2+5\) s koeficienti [1, -10, 0, 5] pa je bolje, da ga definiramo s pomočjo np.poly1d:
numpy.poly1d(c_or_r, r=False, variable=None)
kjer so parametri:
c_or_rkoeficienti polinoma s padajočo potenco ali če jer=Trueničle polinoma,rje privzetoFalse, kar pomeni, da se podajo koeficienti polinoma,variablespremenljivka, ki se izpiše pri uporabi funkcijeprint().
Uvozimo numpy in definirajmo polinom:
import numpy as np # uvozimo numpy
f = np.poly1d([1, -10, 0, 5]) # definiramo koeficiente polinoma
print(f) # prikažemo polinom
3 2
1 x - 10 x + 5
Prikažimo funkcijo \(f(x)\):
import matplotlib.pyplot as plt # uvozimo matplotlib
%matplotlib inline
x_r = np.linspace(-1, 1, 100)
plt.axhline(0, color='r', lw=0.5) # horizontalna črta,
plt.plot(x_r, f(x_r), label='$f(x)$') # da je ničla nekje blizu $x = 0.7$.
plt.legend();
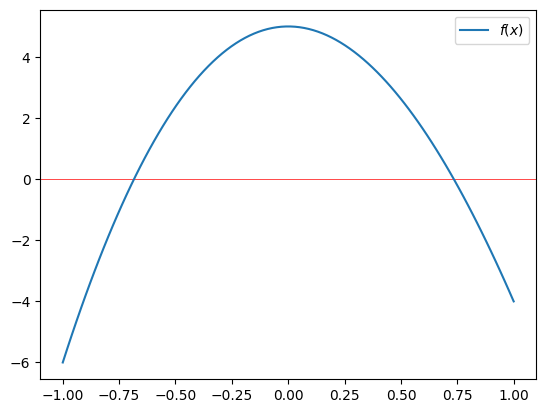
Opazimo, da so ničle funkcije \(f(x)\) blizu -0,7 in +0,7. Objekt poly1d ima atribut roots ali tudi r (glejte dokumentacijo), ki vrne te ničle:
f.r
array([ 9.94949106, 0.73460351, -0.68409457])
V nadaljevanju bo naš cilj numerično določiti ničlo za poljubno funkcijo f.
Inkrementalna metoda#
Inkrementalno reševanje temelji na ideji, da v kolikor ima funkcija \(f(x)\) pri \(x_0\) in \(x_1\) različna predznaka, potem je vmes vsaj ena ničla. Zaprti interval \([x_0, x_1]\) razdelimo torej na odseke širine \(\Delta x\); na odseku, kjer opazimo spremembo predznaka, je vsaj ena ničla funkcije.
Metoda je prikazana na sliki.
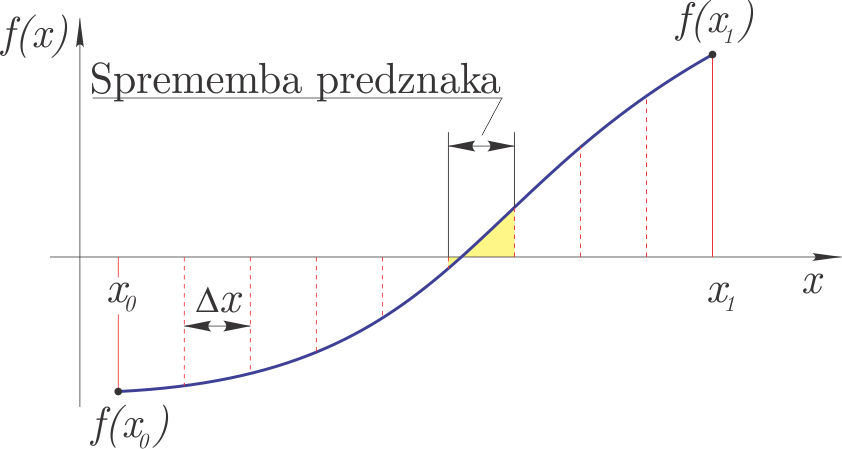
Za ničlo zahtevamo:
kjer je \(\epsilon\) zahtevana natančnost rešitve in \(D\) izbrana majhna vrednost, ki prepreči, da bi kot ničlo razpoznali pol (kar sicer zaradi pogoja zveznosti ni mogoče).
Inkrementalna metoda ima nekatere slabosti:
je zelo počasna,
lahko zgreši dve ničli, ki sta si zelo blizu,
večkratne sode ničle (lokalni ekstrem, ki se samo dotika abscise) ne zazna.
Inkrementalna metoda spada med t. i. zaprte (angl. bracketed) metode, saj išče ničle funkcije samo na intervalu \([x_0, x_1]\). Pozneje bomo spoznali tudi odprte metode, ki lahko konvergirajo k ničli zunaj podanega intervala.
Zaradi vseh zgoraj navedenih slabosti inkrementalno metodo pogosto uporabimo samo za izračun začetnega približka ničle.
Numerična implementacija#
Poglejmo si sedaj inkrementalno iskanje ničel funkcije:
def inkrementalna(fun, x0, x1, dx):
""" Vrne prvi interval (x1, x2) kjer leži ničla
:param fun: funkcija katere ničle iščemo
:param x1: spodnja meja iskanja
:param x2: zgornja meja iskanja
:param dx: inkrement iskanja
"""
x_d = np.arange(x0, x1, dx) # pripravimo x vrednosti
f_d = np.sign(fun(x_d)) # pripravimo predznake funkcije
f_d = f_d[1:]*f_d[:-1] # pomnožimo sosednje elemente
i = np.argmin(f_d) # prvi prehod skozi ničlo
# vsota abs funk vrednosti
x0 = x_d[i]
x1 = x_d[i+1]
D = np.abs(fun(x0)) + np.abs(fun(x1))
return np.asarray([x0, x1]), D
Poglejmo sedaj uporabo na zgoraj definiranem polinomu:
rez_inkr, D = inkrementalna(f, 0., 1., 0.001)
rez_inkr
array([0.734, 0.735])
Ničla je izolirana z natančnostjo 0,001, preverimo še vsoto absolutnih funkcijskih vrednosti:
D
np.float64(0.013071529000000304)
Ugotovimo, da je relativno majhna; bomo pa se s sledečimi metodami trudili rezultat bistveno izboljšati.
Pripravimo sliko:
def fig():
plt.plot(x_r, f(x_r), label='$f(x)$')
plt.axhline(0, color='r', lw=0.5) # horizontalna črta
plt.axvline(rez_inkr[0], color='r', lw=0.5) # vertikalna črta
plt.axvline(rez_inkr[1], color='r', lw=0.5) # vetrikalna črta
plt.plot(rez_inkr, f(rez_inkr), 'ro', label='Inkrementalna metoda')
plt.xlim(0.73,0.74)
plt.ylim(-0.1, 0.1)
plt.legend();
Prikažimo rezultat:
fig()
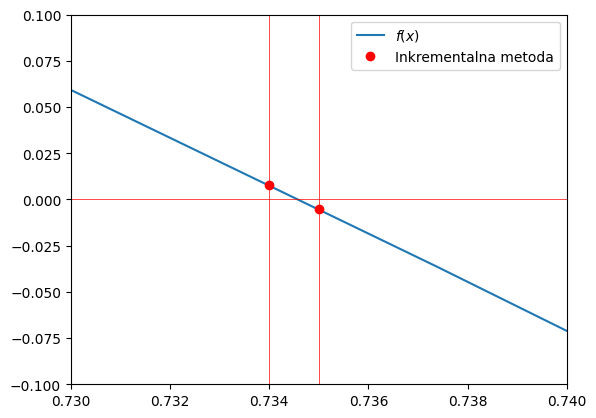
Da smo torej na intervalu \([0, 1]\) izračunali rešitev z natančnostjo \(\Delta x=0,001\), smo morali 1000-krat klicati funkcijo \(f(x)\). Gre za zelo neučinkovito metodo, zato bomo iskali boljše načine; najprej s preprostim iterativnim inkrementalnim pristopom.
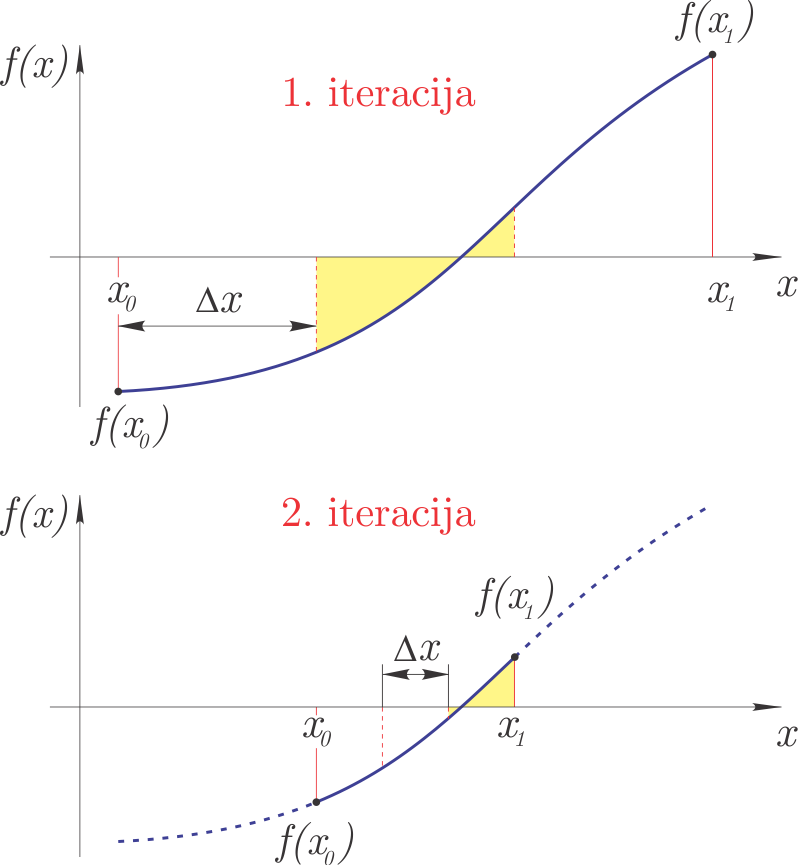
Iterativna inkrementalna metoda#
Iterativna inkrementalna metoda v prvi iteraciji z inkrementalno metodo omeji interval iskanja ničel pri relativno velikem koraku. Interval, najden v prvi iteraciji, se v drugi iteraciji razdeli na manjše intervale in ponovi se inkrementalno iskanje ničle. Tretja iteracija se nato omeji na interval določen v drugi in tako dalje. Z iteracijami zaključimo, ko smo dosegli predpisano natančnost rešitve \(\epsilon\).
Metoda je prikazana na sliki:
Numerična implementacija#
def inkrementalna_super(fun, x0, x1, iteracij=3):
""" Vrne interval (x0, x1) kjer leži ničla
:param fun: funkcija katere ničlo iščemo
:param x0: spodnja meja iskanja
:param x1: zgornja meja iskanja
:iteraci: število iteracij inkrementalne metode
"""
for i in range(iteracij):
dx = (x1 - x0)/10
x0x1, _ = inkrementalna(fun, x0, x1, dx)
x0, x1 = x0x1
# vsota abs funk vrednosti
D = np.abs(fun(x0)) + np.abs(fun(x1))
return np.asarray([x0, x1]), D
S 30 klici funkcije \(f(x)\) tako dobimo podobno natančnost kot prej v 1000:
rez30, D30 = inkrementalna_super(f, 0., 1., iteracij=3)
rez30
array([0.734, 0.735])
rez_inkr
array([0.734, 0.735])
Seveda pa lahko natančnost bistveno izboljšamo z večanjem števila iteracij:
rez80, D80 = inkrementalna_super(f, 0., 1., iteracij=8)
rez80
array([0.7346035 , 0.73460351])
Preverimo še kriterij vsote absolutnih funkcijskih vrednosti, ki mora biti majhen:
D80
np.float64(1.3073143190212022e-07)
Bisekcijska metoda#
Na intervalu \([x_0, x_1]\), kjer vemo, da obstaja ničla funkcije (predznaka \(f(x_0)\) in \(f(x_1)\) se razlikujeta), lahko uporabimo bisekcijsko metodo.
Ideja metode je:
interval \([x_0, x_1]\) razdelimo na pol (od tukaj ime: bi-sekcija): \(x_2 = (x_0+x_1)/2\),
če imata \(f(x_0)\) in \(f(x_2)\) različne predznake, je nov interval iskanja ničle \([x_0, x_2]\), sicer pa: \([x_2, x_1]\),
glede na predhodni korak definiramo nov zaprt interval \([x_0, x_1]\) in nadaljujemo z iterativnim postopkom, dokler ne dosežemo želene natančnosti \(\left|x_1-x_0\right|<\varepsilon\).
Slika metode:
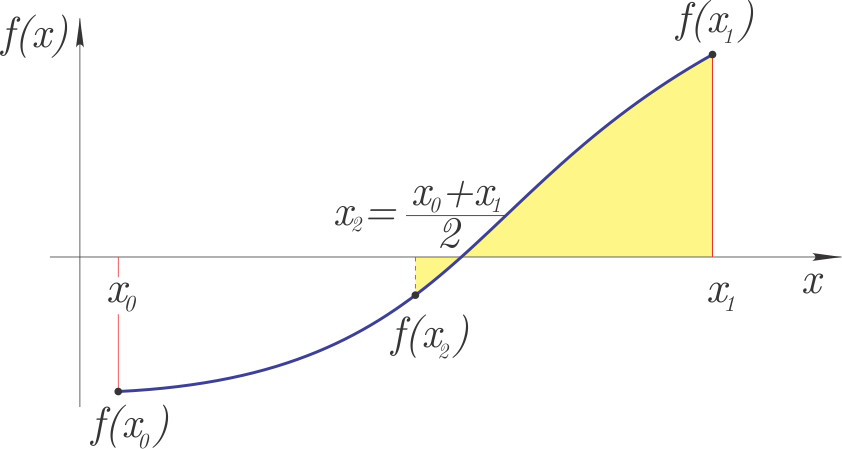
Bisekcijska metoda spada med zaprte metode, ki vrne ničlo funkcije na podanem intervalu \([x_0, x_1]\).
Ocena napake#
Če v začetku začnemo z intervalom \(\Delta x = \left|x_1-x_0\right|\), potem je natančnost bisekcijske metode po prvem koraku bisekcije:
po drugem koraku:
in po \(n\) korakih:
Ponavadi zahtevamo, da je rešitev podana z natančnostjo \(\varepsilon\) in iz zgornje enačbe lahko izpeljemo število potrebnih korakov bisekcijske metode:
Seveda je število korakov celo število.
Numerična implementacija#
def bisekcija(fun, x0, x1, tol=1e-3, Dtol=1e-1, izpis=True):
""" Vrne ničlo z natančnostjo tol
:param fun: funkcija katere ničlo iščemo
:param x0: spodnja meja iskanja
:param x1: zgornja meja iskanja
:param tol: zahtevana natančnost
:param Dtol:največja vsota absolutnih vrednosti rešitve
:izpis: ali na koncu izpiše kratko poročilo
"""
if np.sign(fun(x0))==np.sign(fun(x1)):
raise Exception('Ničla ni izolirana. Root is not bracketed.')
n = np.ceil( np.log(np.abs(x1-x0)/tol)/np.log(2) ).astype(int) # števil iteracij
for i in range(n):
x2 = (x0 + x1) / 2
f1 = fun(x0)
f3 = fun(x2)
f2 = fun(x1)
if np.sign(fun(x2))!=np.sign(fun(x0)):
x1 = x2
else:
x0 = x2
D = np.abs(fun(x0)) + np.abs(fun(x1))
if D > Dtol:
raise Exception('Verjetnost pola ali več ničel.')
r = (x0+x1)/2
if izpis:
decimalk = int(np.log10(1/tol)) # ne deluje vedno in za vse primere:)
print(f'Rešitev: {r:5.{decimalk}f}, število iteracij: {n:g}, D: {D:5.5f}')
return r
Sedaj poskusimo najti ničlo z natančnostjo 1e-3:
bisekcija(f, 0, 1, tol=1e-3);
Rešitev: 0.735, število iteracij: 10, D: 0.01277
V desetih iteracijah smo dobili isto natančen rezultat kakor zgoraj pri iterativni inkrementalni metodi rez30. Poglejmo še izračun ničle s še večjo natančnostjo:
bisekcija(f, 0, 1, tol=1e-6);
Rešitev: 0.734603, število iteracij: 20, D: 0.00001
Hitrost izvajanja lahko preverimo s t. i. magic funkcijo timeit (dokumentacija), ki večkrat požene funkcijo in analizira čas izvajanja. Če je pred magic funkcijo dvojni znak %%, se izvede in meri čas celotne celice, če pa le enojni %, pa samo ene vrstice.
%%timeit
bisekcija(f, 0., 1., izpis=False)
310 μs ± 25.5 μs per loop (mean ± std. dev. of 7 runs, 1,000 loops each)
Iskanje ničle v okolici pola#
Poglejmo sedaj iskanje ničle funkcije tan v okolici pola (ničla dejansko ne obstaja):
x_t = np.linspace(-3, 3, 100)
plt.plot(x_t, np.tan(x_t), label='$\\tan(x)$')
plt.ylim(-10, 10)
plt.legend();
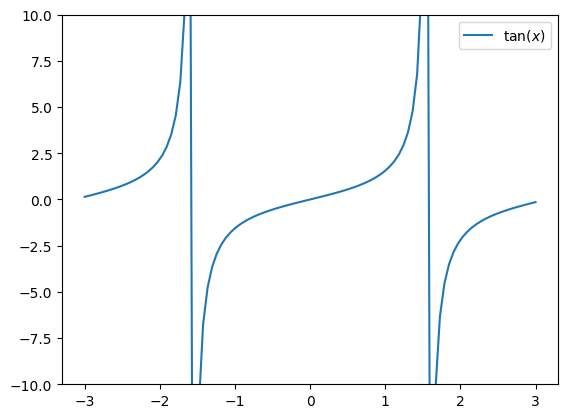
V primeru iskanja na intervalu \([-1, 1]\) najdemo pravo ničlo:
bisekcija(np.tan, -1, 1, tol=1e-3);
Rešitev: -0.000, število iteracij: 11, D: 0.00098
V primeru iskanja v okolici pola, pa nas program na to opozori (klic funkcije je tukaj zakomentiran, sicer se avtomatsko generiranje tukaj prekine):
## bisekcija(np.tan, -3, 0, tol=1e-6)
V scipy vgrajena bisekcijska metoda takega preverjanja nima (zaradi hitrosti) in bo vrnila rezultat, ki bo pa napačen. Pri uporabi moramo torej biti previdni.
Uporaba scipy.optimize.root_scalar#
Bisekcijska metoda je počasna, vendar zanesljiva metoda iskanja ničel in je implementirana znotraj scipy. Najprej jo uvozimo:
from scipy.optimize import root_scalar
root_scalar(f, args=(), method='bisect', bracket=[a,b], fprime=None, fprime2=None, x0=None, x1=None,xtol=None, rtol=None, maxiter=None, options=None)
Da s funkcijo root_scalar prikličemo bisekcijsko metodo moramo funkciji podati tri parametre: funkijo f ter zaprti interval [a, b] (prek parametra bracket). Predznaka f(a) in f(b) morata biti različna. Ostali parametri, npr. absolutna xtol in relativna rtol napaka ter največje število iteracij maxiter so opcijski - imajo privzete vrednosti. Za več glejte dokumentacijo.
Poglejmo uporabo:
root_scalar(f, bracket=[0, 1], method='bisect')
converged: True
flag: converged
function_calls: 41
iterations: 39
root: 0.7346035077880515
method: bisect
in hitrost:
%timeit root_scalar(f, bracket=[0, 1], method='bisect')
319 μs ± 44.4 μs per loop (mean ± std. dev. of 7 runs, 1,000 loops each)
Preverimo še lahko funkcijo tan(x), najprej na intervalu, kjer je funkcija zvezna:
root_scalar(np.tan, bracket=[-1, 1], method='bisect')
converged: True
flag: converged
function_calls: 3
iterations: 1
root: 0.0
method: bisect
Potem še v okolici pola, kjer ni zvezna:
root_scalar(np.tan, bracket=[-3, -1], method='bisect')
converged: True
flag: converged
function_calls: 42
iterations: 40
root: -1.5707963267941523
method: bisect
kar je napačna rešitev!
Sekantna metoda#
Sekantna metoda zahteva dva začetna približka \(x_0\) in \(x_1\) in funkcijo \(f(x)\). Ob predpostavki linearne interpolacije med točkama \(x_0, f(x_0)\) in \(x_1, f(x_1)\) (skozi točki potegnemo sekanto, od tukaj tudi ime), se določi \(x_2\), kjer ima linearna interpolacijska funkcija ničlo. \(x_2\) predstavlja nov približek ničle.
Glede na sliko:
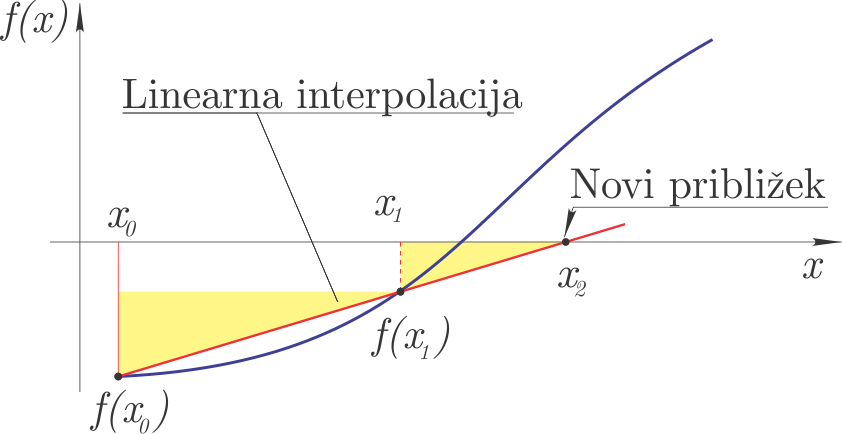
lahko zapišemo (podobna trikotnika sta na sliki označena z rumeno):
Sledi, da je nov približek ničle:
V naslednjem koraku pri sekantni metodi izvedemo sledeče zamenjave: \(x_0=x_1\) in \(x_1=x_2\).
Sekantna metoda spada med odprte metode, saj lahko najde ničlo funkcije, ki se nahaja zunaj območja \([x_0, x_1]\).
Ocena napake#
Konzervativno lahko napako ocenimo iz razlike med dvema zaporednima približkoma:
Konvergenca in red konvergence#
Konvergenca pomeni, da zaporedje približkov konvergira k rešitvi enačbe \(\alpha\) (\(\alpha\) je rešitev enačbe).
Red konvergence označuje hitrost konvergiranja.
Če \(\varepsilon\) označimo napako približka in napako z vsakim korakom iteracije linearno zmanjšamo (\(C\) je konstanta):
govorimo o redu konvergence 1 (\(\varepsilon\) ima potenco 1)!
Pri predhodno obravnavani bisekcijski metodi napako na vsakem koraku zmanjšamo za \(1/2\) (\(\varepsilon_n/\varepsilon_{n-1} = C = 1/2\)). Bisekcijska metoda ima red konvergence 1.
Red konvergence sekantne metode je višji in jo je mogoče oceniti z:
Iz zgornje ocene sledi, da se na vsakem koraku iteracije število točnih cifer poveča za približno 60%. Ker je red konvergence višji od 1 in manjši od kvadratične, tako konvergenco imenujemo superlinearna konvergenca.
Numerična implementacija#
def sekantna(fun, x0, x1, tol=1e-3, Dtol=1e-1, max_iter=50, izpis=True):
""" Vrne ničlo z natančnostjo tol
:param fun: funkcija katere ničlo iščemo
:param x0: spodnja meja iskanja
:param x1: zgornja meja iskanja
:param tol: zahtevana natančnost
:max_iter: maksimalno število iteracij preden se izvajanje prekine
:param Dtol:največja vsota absolutnih vrednosti rešitve
:izpis: ali na koncu izpiše kratko poročilo
"""
if np.sign(fun(x0))==np.sign(fun(x1)):
raise Exception('Ničla ni izolirana. Root is not bracketed.')
for i in range(max_iter):
f0 = fun(x0)
f1 = fun(x1)
x2 = x1 - f1 * (x1 - x0)/(f1 - f0)
x0 = x1
x1 = x2
if izpis:
print('{:g}. korak: x0={:g}, x1={:g}.'.format(i+1, x0, x1))
if np.abs(x1-x0)<tol:
r = (x0+x1)/2
D = np.abs(fun(x0)) + np.abs(fun(x1))
if D > Dtol:
raise Exception('Verjetnost pola ali več ničel.')
r = (x0+x1)/2
if izpis:
decimalk = int(np.log10(1/tol)) # ne deluje vedno in za vse primere:)
print(f'Rešitev: {r:5.{decimalk}f}, D: {D:5.5f}')
return r
Poglejmo si uporabo:
sekantna(f, 0, 1., tol=1.e-8, izpis=True);
1. korak: x0=1, x1=0.555556.
2. korak: x0=0.555556, x1=0.707845.
3. korak: x0=0.707845, x1=0.737957.
4. korak: x0=0.737957, x1=0.734549.
5. korak: x0=0.734549, x1=0.734603.
6. korak: x0=0.734603, x1=0.734604.
7. korak: x0=0.734604, x1=0.734604.
Rešitev: 0.73460351, D: 0.00000
in hitrost
%timeit sekantna(f, 0, 1., tol=1.e-8, izpis=False)
132 μs ± 9.39 μs per loop (mean ± std. dev. of 7 runs, 10,000 loops each)
Kakor smo zapisali zgoraj, je sekantna metoda odprtega tipa. Rešitev enačbe je lahko zunaj podanega intervala. Poglejmo si primer:
sekantna(np.tan, 1, 2);
1. korak: x0=2, x1=1.41615.
2. korak: x0=1.41615, x1=1.85165.
3. korak: x0=1.85165, x1=1.69887.
4. korak: x0=1.69887, x1=1.97485.
5. korak: x0=1.97485, x1=2.09379.
6. korak: x0=2.09379, x1=2.43519.
7. korak: x0=2.43519, x1=2.76579.
8. korak: x0=2.76579, x1=3.05013.
9. korak: x0=3.05013, x1=3.13625.
10. korak: x0=3.13625, x1=3.14158.
11. korak: x0=3.14158, x1=3.14159.
Rešitev: 3.142, D: 0.00002
Uporaba scipy.optimize.root_scalar#
Znotraj scipy je sekantna metoda definirana v okviru scipy.optimize.root_scalar funkcije:
root_scalar(f, x0=1, method='secant')
converged: True
flag: converged
function_calls: 7
iterations: 6
root: 0.7346035077893033
method: secant
V primeru sekantne metode, se druga meja intervala izračuna glede na kodo:
if x0 >= 0:
x1 = x0*(1 + 1e-4) + 1e-4
else:
x1 = x0*(1 + 1e-4) - 1e-4
Poglejmo še hitrost
%timeit root_scalar(f, x0=1, method='secant')
111 μs ± 7.21 μs per loop (mean ± std. dev. of 7 runs, 10,000 loops each)
Sorodna sekantni metodi je Ridderjeva metoda; v podrobnosti metode tukaj ne gremo, je pa zaprtega tipa, ima kvadratičen red konvergence ter jo kličemo s pomočjo funkcije root_scalar:
root_scalar(f, bracket=[0, 1], method='ridder')
converged: True
flag: converged
function_calls: 14
iterations: 6
root: 0.7346035077883111
method: ridder
Brentova metoda (brentq) je v Scipy privzeta in priporočena izbira za iskanje ničel na intervalu. Združuje zanesljivost bisekcije in hitrost sekantne metode/inverzne kvadratne interpolacije. Uporaba in hitrost:
root_scalar(f, bracket=[0, 1], method='brentq')
converged: True
flag: converged
function_calls: 9
iterations: 8
root: 0.7346035077893034
method: brentq
Primerjava hitrosti kaže, da je običajno hitrejša od bisekcije:
%timeit root_scalar(f, bracket=[0, 1], method='brentq')
81.7 μs ± 6.84 μs per loop (mean ± std. dev. of 7 runs, 10,000 loops each)
Sicer pa Scipy podpira tudi algoritem TOMS 748, ki velja za asimptotično najučinkovitejšo metodo za iskanje ničel na intervalu:
root_scalar(f, bracket=[0, 1], method='toms748')
converged: True
flag: converged
function_calls: 9
iterations: 4
root: 0.7346035077893033
method: toms748
Primerjava hitrosti (v večini primerov bi naj bila najhitrejša):
%timeit root_scalar(f, bracket=[0, 1], method='toms748')
454 μs ± 48.9 μs per loop (mean ± std. dev. of 7 runs, 1,000 loops each)
Newtonova metoda#
Doslej predstavljene metode ne zahtevajo dodatnih odvodov funkcije; Newtonova metoda, ki si jo bomo pogledali v nadaljevanju, zahteva en začetni približek \(x_0\), poleg definicije funkcije \(f(x)\) pa tudi njen odvod \(f'(x)\). V literaturi za Newtonovo metodo tudi najdemo izraza tangentna in Newton-Raphsonova metoda.
Princip delovanja metode je prikazan na sliki:
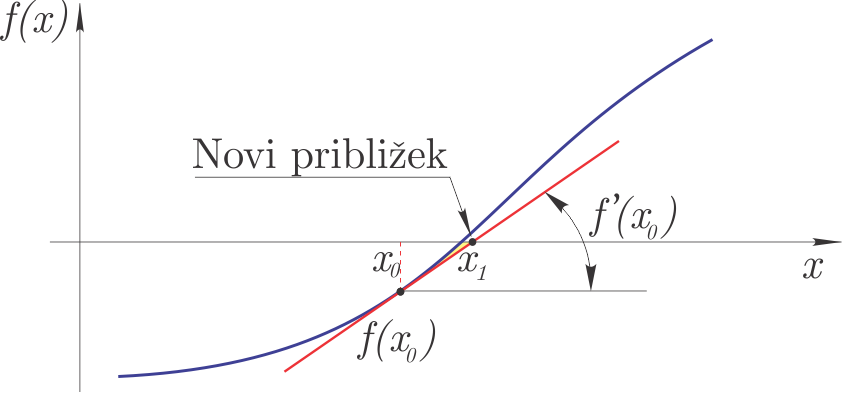
Metodo bi lahko izpeljali grafično (s slike), tukaj pa si poglejmo izpeljavo s pomočjo Taylorjeve vrste:
če naj bo pri \(x_{i+1}\) vrednost funkcije nič, potem velja:
Naredimo napako metode in zanemarimo člene višjega reda v Taylorjevi vrsti. Lahko izpeljemo:
\(x_{i+1}\) je tako nov približek iskane ničle.
Algoritem Newtonove metode je:
izračunamo nov približek \(x_{i+1}\),
računanje prekinemo, če je največje število iteracij doseženo (rešitve enačbe nismo našli),
če velja \(\left|x_{i+1}-x_i\right|<\varepsilon\) računanje prekinemo (izračunali smo približek ničle), sicer povečamo indeks \(i\) in gremo v prvi korak.
Opombi:
\(\varepsilon\) je zahtevana absolutna natančnost,
Newtonova metoda lahko divergira, zato v algoritmu predpišemo največje število iteracij.
Zgoraj smo omenili, da je Newtonova metoda ena izmed boljših metod za iskanje ničel funkcij. Ima pa tudi nekaj slabosti/omejitev:
spada med odprte metode,
kvadratična konvergenca je zagotovljena le v dovolj majhni okolici rešitve enačbe,
poznati moramo odvod funkcije.
Red konvergence#
Red konvergence Newtonove metode je kvadraten:
kjer je \(C\):
Konvergenca je torej hitra, v vsaki novi iteraciji se število točnih števk v približku podvoji.
Numerična implementacija#
def newtonova(fun, dfun, x0, tol=1e-3, Dtol=1e-1, max_iter=50, izpis=True):
# ime `newtonova` zato ker je `newton` vgrajena funkcija v `scipy`
""" Vrne ničlo z natančnostjo tol
:param fun: funkcija katere ničlo iščemo
:param dfun: f'
:param x0: začetni približek
:param tol: zahtevana natančnost
:max_iter: maksimalno število iteracij preden se izvajanje prekine
:param Dtol:največja vsota absolutnih vrednosti rešitve
:izpis: ali na koncu izpiše kratko poročilo
"""
for i in range(max_iter):
x1 = x0 - fun(x0)/dfun(x0)
if np.abs(x1-x0)<tol:
r = (x0+x1)/2
D = np.abs(fun(x0)) + np.abs(fun(x1))
if D > Dtol:
raise Exception('Verjetnost pola ali več ničel.')
if izpis:
decimalk = int(np.log10(1/tol)) # ne deluje vedno in za vse primere:)
print(f'Rešitev: {x1:5.{decimalk}f}, število iteracij: {i+1}, D: {D:5.8f}')
return x1
x0 = x1
raise Exception('Metoda po {:g} iteracijah ne konvergira'.format(max_iter))
Definirajmo polinom f in njegov prvi odvod df:
def f(x):
return x**3 - 10*x**2 + 0*x + 5
def df(x):
return 3*x**2 - 20*x
Izračunajmo sedaj ničlo:
newtonova(fun=f, dfun=df, x0=1, tol=1e-8);
Rešitev: 0.73460351, število iteracij: 5, D: 0.00000000
Preverimo hitrost izvajanja:
%timeit newtonova(fun=f, dfun=df, x0=1, tol=1e-8, izpis=False)
8.07 μs ± 499 ns per loop (mean ± std. dev. of 7 runs, 100,000 loops each)
Uporaba scipy.optimize.root_scalar#
Znotraj scipy je Newtonova metoda definirana v okviru scipy.optimize.root_scalar funkcije:
root_scalar(f, x0=1, method='newton', fprime=df)
converged: True
flag: converged
function_calls: 10
iterations: 5
root: 0.7346035077893033
method: newton
In izmerimo hitrost:
%timeit root_scalar(f, x0=1, method='newton', fprime=df)
56.1 μs ± 2.89 μs per loop (mean ± std. dev. of 7 runs, 10,000 loops each)
Če pri root_scalar podamo tudi drugi odvod fprime2, se uporabi Halleyeva metoda, ki temelji na izrazu:
def ddf(x):
return 6*x - 20
root_scalar(f, x0=1, method='halley', fprime=df, fprime2=ddf)
converged: True
flag: converged
function_calls: 10
iterations: 3
root: 0.7346035077893033
method: halley
In hitrost:
%timeit root_scalar(f, x0=1, method='halley', fprime=df, fprime2=ddf)
42.8 μs ± 2.78 μs per loop (mean ± std. dev. of 7 runs, 10,000 loops each)
Poglejmo si primer uporabe Newtonove metode v scipy.optimize:
Reševanje sistemov nelinarnih enačb*#
Rešujemo sistem enačb, ki ga v vektorski obliki zapišemo takole:
V skalarni obliki zgornji vektorski izraz zapišemo:
Reševanje sistema \(n\) nelinearnih enačb je bistveno bolj zahtevno kot reševanje ene same nelinearne enačbe. Tak sistem enačb ima lahko več rešitev in katero izračunamo, je odvisno od začetnih pogojev. Ponavadi nam pri dobri izbiri začetnih pogojev pomaga fizikalni problem, ki ga rešujemo.
Za računanje rešitve sistema enačb se Newtonova metoda izkaže kot najenostavnejša in pogosto tudi najboljša (obstajajo tudi druge metode, ki pa so velikokrat variacije Newtonove metode).
Podobno kot pri izpeljavi Newtonove metode za reševanje ene enačbe, tudi tukaj začnemo z razvojem funkcije \(f_i\) v Taylorjevo vrsto:
Naredimo napako metode, ko zanemarimo člene drugega in višjih redov ter zapišemo izraz v matrični obliki:
kjer je \(\mathbf{J}(\mathbf{x})\) Jakobijeva matrika pri vrednostih \(\mathbf{x}\). Elementi Jakobijeve matrike so:
Če naj bo \(\mathbf{x}+\Delta \mathbf{x}\) rešitev sistema enačb, mora veljati:
in torej sledi:
Izpeljali smo sistem linearnih enačb, matrika koeficientov je označena z \(\mathbf{J}(\mathbf{x})\), vektor neznank je \(\Delta\mathbf{x}\) in vektor konstant \(-\mathbf{f}(\mathbf{x}).\)
Opomba: analitično računanje Jakobijeve matrike je lahko zamudno in zato jo pogosto približno izračunamo pri \(\mathbf{x}\) numerično:
kjer je \(h\) majhen premik in je \(\mathbf{e}_j\) enotski pomik v smeri \(x_j\). Če se Jakobijeva matrika izračuna numerično, govorimo o sekantni metodi in ne Newtonovi.
Pri numeričnem izračunu si lahko pomagamo s funkcijo scipy.optimize.approx_fprime (za podrobnosti glejte dokumentacijo).
Numerična implementacija#
Algoritem torej je:
Izberemo začetni približek \(\mathbf{x}_0\), največje število iteracij in postavimo indeks na nič: \(i=0\).
Izračunamo Jakobijevo matriko \(\mathbf{J}(\mathbf{x_i})\) in rešimo linearni sistem: \(\mathbf{J}(\mathbf{x}_i)\,\Delta \mathbf{x}_i=-\mathbf{f}(\mathbf{x}_i)\).
Izračunamo nov približek: \(\mathbf{x}_{i+1}=\mathbf{x}_{i}+\Delta\mathbf{x}_i\).
Če je napaka manjša od zahtevane, se postopek prekine*. Postopek prekinemo tudi, če je število iteracij večje od dovoljenega, sicer povečamo indeks \(i=i+1\) in se vrnemo v korak 2.
* Opomba:
Napako lahko ocenimo z normo razlike dveh zaporednih približkov:
kjer je \(i\) indeks iteracije in \(j\) indeks elementa.
Uporaba scipy.optimize.root#
Funkcija scipy.optimize.root ima obsežno dokumentacijo in omogoča večje število različnih pristopov:
root(fun, x0, args=(), method='hybr', jac=None, tol=None, callback=None, options=None)
Če uporabimo privzete parametre, moramo definirati zgolj vektorsko funkcijo fun in začetno vrednost x0.
Uvozimo funkcijo:
from scipy.optimize import root
Poglejmo si uporabo na zgledu (gre za zgled na str. 76, Jože Petrišič, Reševanje enačb, 1996, FS, UNI-LJ):
kjer je vektor \(\mathbf{x}=[x_0, x_1]\).
Najprej definirajmo Python funkcijo, ki vrne seznam rezultatov funkcij \([f_0(\mathbf{x}),f_1(\mathbf{x})]\):
def func(x):
return [x[0]**2 + x[0]*x[1] -10,
x[1] +3*x[0]*x[1]**2 - 57]
Definirajmo še Jakobijevo matriko:
def J(x):
return np.array([[2*x[0]+x[1], x[0]],
[3*x[1]**2, 1+6*x[0]*x[1]]])
Uporabimo začetne vrednosti \(x_0=1,5\) in \(x_1=3,5\) ter rešimo problem:
rešitev = root(fun=func, x0=[1.5, 3.5], jac=J)
rešitev
message: The solution converged.
success: True
status: 1
fun: [-6.972e-12 3.148e-11]
x: [ 2.000e+00 3.000e+00]
method: hybr
nfev: 12
njev: 1
fjac: [[-2.235e-01 -9.747e-01]
[ 9.747e-01 -2.235e-01]]
r: [-2.954e+01 -3.782e+01 -6.940e+00]
qtf: [-2.836e-08 -1.324e-08]
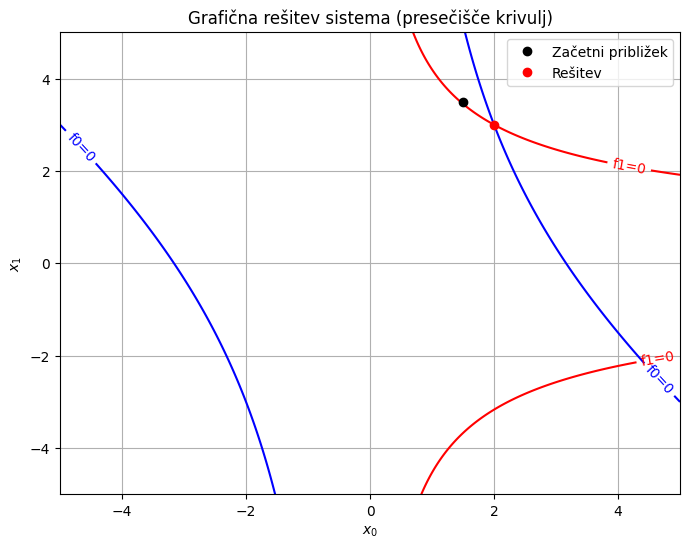
Funkcija root vrne obsežen rezultat. Najbolj pomembna sta atribut x, ki predstavlja iskano rešitev, in atribut success, ki pove, ali je rešitev konvergirala:
rešitev.x
array([2., 3.])
rešitev.success
True
import matplotlib.pyplot as plt
# Priprava mreže točk
x0_range = np.linspace(-5, 5, 400)
x1_range = np.linspace(-5, 5, 400)
X0, X1 = np.meshgrid(x0_range, x1_range)
# Definicija funkcij sistema
F0 = X0**2 + X0*X1 - 10
F1 = X1 + 3*X0*X1**2 - 57
plt.figure(figsize=(8, 6))
# Izris ničelnih izolinij (kjer je f(x) = 0)
CS0 = plt.contour(X0, X1, F0, levels=[0], colors='blue')
CS1 = plt.contour(X0, X1, F1, levels=[0], colors='red')
# Označbe
plt.clabel(CS0, inline=1, fontsize=10, fmt='f0=0')
plt.clabel(CS1, inline=1, fontsize=10, fmt='f1=0')
plt.plot(1.5, 3.5, 'ko', label='Začetni približek')
plt.plot(rešitev.x[0], rešitev.x[1], 'ro', label='Rešitev')
plt.xlabel('$x_0$')
plt.ylabel('$x_1$')
plt.title('Grafična rešitev sistema (presečišče krivulj)')
plt.grid(True)
plt.legend()
plt.show()
Dodatno#
Tisti, ki ste navdušeni nad Raspberry Pi in uporabljate njihovo kamero (npr. tole brez infrardečega filtra), vas bo morebiti zanimala knjižnica picamera.
Uporaba sympy.solve za reševanje enačb#
Za manjše sisteme lahko rešitev najdemo tudi simbolno. Poglejmo si zgornji primer:
import sympy as sym
sym.init_printing()
x, y = sym.symbols('x, y')
funkcije = [x**2 + x*y -10, y + 3*x*y**2 -57]
funkcije
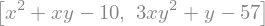
sol = sym.solve(funkcije, x, y)
print(f'Število rešitev: {len(sol)}')
print(f'Prva rešitev: {sol[0]}')
Število rešitev: 4
Prva rešitev: (2, 3)
Vprašanja za vaje#
Primer 1: Porazdelitev tlaka vzdolž krila modela letala aproksimiramo s premico:

Notranji upogibni moment za prikazan primer je definiran kot:
Zanima nas, pri kateri oddaljenosti od trupa letala \(x\) je krilo maksimalno in minimalno upogibno obremenjeno.
Poiščimo prave rešitve najprej s pomočjo Sympy (Pozor: tukaj ne gre za numerično reševanje enačb!).
Numerično reševanje enačb (iskanje ničel)#
Bisekcijska metoda#
Vprašanje 2: Z uporabo bisekcijske metode določite ničle upogibnega momenta \(M(x)\) na intervalu \([0, l]\). Primerjajte rezultate s simbolno dobljenimi in komentirajte rezultat. Dolžina krila \(l=1 m\).
Vprašanje 3: Poiščite ekstreme funkcije \(M(x)\) na intervalu \([0 ,l]\).
Komentirajte ustreznost bisekcijske metode za iskanje ničel \(f(x)\) v našem primeru. Rezultate lahko preverite s pomočjo knjižnjice Sympy.
Vprašanje 4: Lastno nihanje sistema mase in vzmeti opišemo z enačbo:
Z uporabo bisekcijske metode poiščite vse vrednosti časa \(t\) na intervalu \(t \in [0, 20] \, s\), pri katerih je nihalo v ravnovesni legi.
Vprašanje 5: Nalogo 3 rešite tudi z uporabo Ridderjeve metode iz paketa scipy. Primerjajte hitrost Ridderjeve metode z metodo bisekcije iz scipy.
Sekantna metoda#
Vprašanje 6: Z uporabo sekantne metode določite vse ničle \(M(x)\) na intervalu \([0, l]\) (pomagate si lahko z grafičnim prikazom).
Vprašanje 7: Izračunati želite lastne frekvence nosilca na sliki v upogibni smeri.

V literaturi ste prebrali, da velja:
za določitev lastnih frekvenc pa je potrebno poiskati presečišča krivulj:
\(\tanh(\beta l) = \tan(\beta l)\).
Z uporabo bisekcijske in sekantne metode iz modula scipy določite vrednosti \(\beta l\) na območju \(\beta l \in [0, 11]\), ki rešijo zgornjo enačbo. Uporabite podane vrednosti začetnih približkov in območij.
# Podatki
obmocja = [[3, 4.5], [6, 7.5], [10, 10.5]]
zacetni_priblizki = [2, 6, 10]
Newton-Raphsonova metoda#
Vprašanje 8: Poiščite vse tri ničle funkcije iz prejšnje naloge z uporabo metode Newton-Raphson.
Funkcijo prvega odvoda določite s pomočjo orodij Sympy, pomagajte si s funkcijo sym.lambdify(x, f, 'numpy'). Uporabite podane vrednosti začetnih približkov.
# Podatki
x = sym.symbols('x')
f_sym = sym.tanh(x) - sym.tan(x)
zacetni_priblizki = [2, 6, 10]
Sistemi nelinearnih enačb#
Vprašanje 9: S pomočjo scipy.optimize.root poiščite rešitev sistema nelinearnih enačb:
Za vrednosti začetnih približkov izberite: \(x_0 = 2, \quad y_0 = 0\)
