Interpolacija

Uvod

Pri interpolaciji izhajamo iz tabele (različnih) vrednosti \(x_i, y_i\):

\(\mathbf{x}\)	\(\mathbf{y}\)
\(x_0\)	\(y_0\)
\(x_1\)	\(y_1\)
\(\dots\)	\(\dots\)
\(x_{n-1}\)	\(y_{n-1}\)

določiti pa želimo vmesne vrednosti. Če želimo določiti vrednosti zunaj območja \(x\) v tabeli, govorimo o ekstrapolaciji.

V okviru interpolacije (angl. interpolation) točke povežemo tako, da predpostavimo neko funkcijo in dodamo pogoj, da funkcija mora potekati skozi podane točke.

Pri aproksimaciji (angl. approximation ali tudi curve fitting) pa predpostavimo funkcijo, ki se čimbolj (glede na izbrani kriterij) prilega podatkom.

Poglejmo si primer:

\(\mathbf{x}\)	\(\mathbf{y}\)
1.0	0.54030231
2.5	-0.80114362
4.0	-0.65364362

Pri interpolaciji izhajamo iz tabele vrednosti. Da bomo pozneje lahko enostavno prikazali napako, smo zgornjo tabelo generirali s pomočjo izraza \(y = \cos(x)\)!

Pripravimo numerični zgled; najprej uvozimo pakete:

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

Nato pripravimo tabelo ter prikaz:

n = 3
x = np.linspace(1, 4, n)
f = np.cos # posplošimo interpolirano funkcijo (lahko spremenite v drugo funkcijo)
f_ime = f.__str__().split('\'')[1] # avtomatsko vzamemo ime funkcije
y = f(x)# + np.random.rand(len(x))*0.3
plt.plot(x, y, 'o', label='Interpolacijske točke');
plt.legend();

Interpolacija s polinomom

Interpolacija s polinomom se zdi najbolj primerna, saj je enostavna!

Polinom stopnje \(n-1\):

\[ y = a_0\,x^{n-1} +a_1\,x^{n-2} +\cdots + a_{n-2}\,x + a_{n-1}. \]

je definiran z \(n\) konstantami \(a_i\). Da določimo \(n\) konstant, potrebujemo \(n\) (različnih) enačb. Za vsak par \(x_i, y_i\) lahko torej zapišemo:

\[ y_i = a_{0}\,x_i^{n-1} +a_{1}\,x_i^{n-2} +\cdots + a_{n-2}\,x_i + a_{n-1}. \]

Ker imamo podanih \(n\) parov, lahko določimo \(n\) neznanih konstant \(a_i\), ki definirajo polinom stopnje \(n-1\). Sistem \(n\) linearnih enačb lahko zapišemo: $\( \begin{bmatrix} x_{0}^{n-1}&x_{0}^{n-2}&\dots&x_{0}^0\\ x_{1}^{n-1}&x_{1}^{n-2}&\dots&x_{1}^0\\ &&\vdots&&\\ x_{n-1}^{n-1}&x_{n-1}^{n-2}&\dots&x_{n-1}^0\\ \end{bmatrix} \begin{pmatrix} a_{0}\\ a_{1}\\ \vdots\\ a_{n-1} \end{pmatrix}= \begin{pmatrix} y_{0}\\ y_{1}\\ \vdots\\ y_{n-1} \end{pmatrix} \)$

Sistem linearnim enačb zapišemo v obliki:

\[ \mathbf{M}\,\mathbf{a}=\mathbf{b}. \]

Definirajmo matriko koeficientov \(\mathbf{M}\):

M = np.asarray([[_**p for p in reversed(range(len(x)))] for _ in x])
M  

array([[ 1.  ,  1.  ,  1.  ],
       [ 6.25,  2.5 ,  1.  ],
       [16.  ,  4.  ,  1.  ]])

Izračunamo koeficiente \(a_{0}, a_{1},\dots\):

resitev = np.linalg.solve(M, y)
resitev

array([ 0.33087687, -2.05236633,  2.26179176])

Pripravimo interpolacijski polinom kot Pythonovo funkcijo:

def y_function(x, resitev):
    A = np.asarray([[_**p for p in reversed(range(len(resitev)))] for _ in x])
    return A.dot(resitev)

Izris interpolacijskega polinoma pri bolj gosti mreži točk:

xint = np.linspace(np.min(x), np.max(x), 50)
yint = y_function(xint, resitev)
plt.plot(x, y, 'o', label='Interpolacijske točke')
plt.plot(xint, yint, '.',label='Interpolacija')
plt.legend();

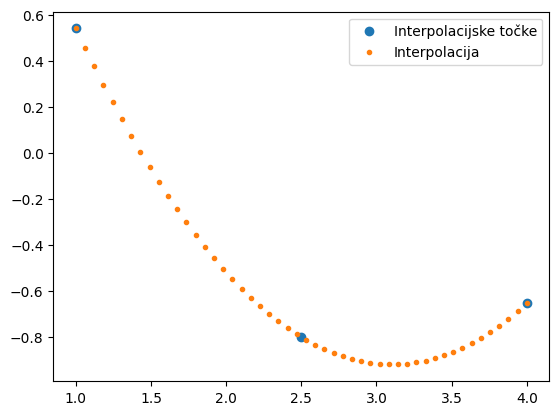
Slabosti zgornjega postopka so:

• število numeričnih operacij raste sorazmerno z \(n^3\),

• problem je lahko slabo pogojen (z večanjem stopnje polinoma slaba pogojenost naglo narašča):

np.linalg.cond(M)

np.float64(71.3022787031108)

Navodilo: vrnite se par vrstic nazaj in spremenite število interpolacijskih točk \(n\) na višjo vrednost (npr. 10).

Lagrangeva metoda

Lagrangeva metoda ne zahteva reševanja sistema enačb in je s stališča števila računskih operacij (narašča sorazmerno z \(n^2\) (vir)) boljša od predhodno predstavljene polinomske interpolacije (število operacij narašča sorazmerno z \(n^3\)), kjer smo reševali sistem linearnih enačb. Rešitev pa je seveda popolnoma enaka!

from IPython.display import YouTubeVideo
YouTubeVideo('c_TbU8XBHsw', width=800, height=300)

Lagrangev interpolacijski polinom stopnje \(n-1\) je definiran kot:

\[ P_{n-1}(x)=\sum_{i=0}^{n-1}y_i\,l_i(x), \]

kjer je \(l_i\) Lagrangev polinom:

\[ l_i(x)=\prod_{j=0, j\ne i}^{n-1} \frac{x-x_j}{x_i-x_j}. \]

Poglejmo si interpolacijo za zgoraj prikazane \(x\) in \(y\) podatke.

Definirajmo najprej Lagrangeve polinome \(l_i(x)=\prod_{j=0, j\ne i}^{n-1} \frac{x-x_j}{x_i-x_j}\):

def lagrange(x, x_int, i):
    """ Vrne vrednosti i-tega Lagrangevega polinoma
    
    x: neodvisna spremenljivka (skalar ali numerično polje)
    x_int: seznam interpolacijskih točk
    i: indeks polinoma
    """
    Lx = 1.0
    for j in range(len(x_int)):
        if j != i:
            Lx *= (x-x_int[j]) / (x_int[i]-x_int[j])
    return Lx

def slika(i=0):
    xint = np.linspace(np.min(x), np.max(x), 30)
    plt.plot(x, y, 'o', label='Interpolacijske točke')
    plt.axhline(0, color='k', linewidth=0.3);
    plt.plot(xint, lagrange(xint, x_int=x, i=i), '.',label=f'Lagrangev polinom i={i}');
    for _ in x:
        plt.axvline(_, color='r', linewidth=0.5);
    plt.legend()
    plt.show()

slika(i=1)

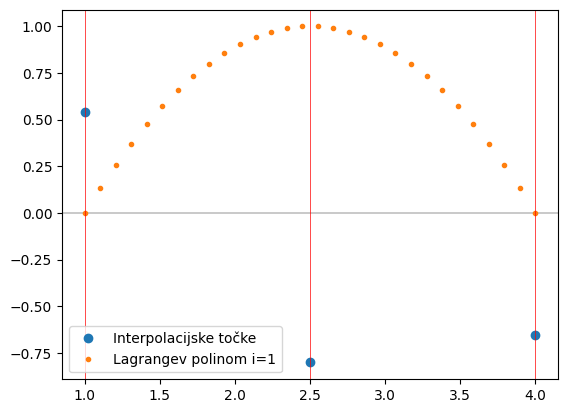
Opazimo, da ima \(i\)-ti Lagrangev polinom v \(x_i\) vrednost 1, v ostalih podanih točkah pa nič!

Če torej Lagrangev polinom za \(i=0\) pomnožimo z \(y_0\), bomo pri \(x=x_0\) dobili pravo vrednost, v ostalih interpolacijskih točkah pa nič; implementirajmo torej Lagrangev interpolacijski polinom:

\[ P_{n-1}(x)=\sum_{i=0}^{n-1}y_i\,l_i(x), \]

def lagrange_interpolacija(x, x_int, y_int):
    """ Vrne vrednosti Lagrangeve interpolacije
    
    x: neodvisna spremenljivka (skalar ali numerično polje)
    x_int: abscisa interpolacijskih točk
    y_int: ordinata interpolacijskih točk
    """
    y = 0.
    for i in range(len(x_int)):
        Lx = 1.0
        for j in range(len(x_int)):
            if j != i:
                Lx *= (x-x_int[j]) / (x_int[i]-x_int[j])
        y += y_int[i] * Lx
    return y

Pripravimo sliko:

def slika(i=0):
    xint = np.linspace(np.min(x), np.max(x), 30)
    plt.plot(x, y, 'o', label='Interpolacijske točke')
    plt.plot(xint, lagrange(xint, x_int=x, i=i), '.',label=f'Lagrangev polinom i={i}');
    plt.plot(xint, lagrange_interpolacija(xint, x_int=x, y_int=y), '.',label=f'Lagrangev int polinom');
    plt.axhline(0, color='k', linewidth=0.3);
    for _ in x:
        plt.axvline(_, color='r', linewidth=0.5);
    plt.legend()
    plt.show()

Iz ipywidgets uvozimo interact, ki je močno orodje za avtomatsko generiranje (preprostega) uporabniškega vmesnika znotraj jupyter okolja. Tukaj bomo uporabili relativno preprosto interakcijo s sliko; za pregled vseh zmožnosti pa radovednega bralca naslavljamo na dokumentacijo.

Uvoz funkcije interact

from ipywidgets import interact

interact(slika);

Iz slike vidimo, da ima Lagrangev polinom \(i\) samo pri \(x_i\) vrednost 1 v ostalih točkah \(\ne i\) pa ima vrednosti nič; ko Lagrangev polinom \(l_i(x)\) pomnožimo z \(y_i\) zadostimo \(i\)-ti točki iz tabele. Posledično Lagrangeva interpolacija z vsoto Lagrangevih polinomov interpolira tabelo.

Polinomska interpolacija pri velikem številu točk je lahko slabo pogojena naloga in zato jo odsvetujemo.

Ocena napake

Če je \(f(x)\) funkcija, ki jo interpoliramo in je \(P_{n-1}(x)\) interpolacijski polinom stopnje \(n-1\), potem se lahko pokaže (glejte npr.: Burden, Faires, Burden: Numerical Analysis), da je napaka interpolacije s polinomom:

\[ e=f(x)-P_{n-1}(x)=\frac{f^{(n)}(\xi)}{n!}\,(x-x_0)\,(x-x_1)\,\cdots\,(x-x_{n-1}), \]

kjer je \(f^{(n)}\) odvod funkcije, \(n-1\) stopnja interpolacijskega polinoma in \(\xi\) vrednost na interpoliranem intervalu \([x_0, x_{n-1}]\).

Zgled

Tukaj si bomo ogledali interpolacijo točk:

x = np.array([0.        ,  0.52359878,  1.04719755,  1.57079633])
y = np.array([ 0.       ,  0.5      ,  0.8660254,  1.       ])

Točke prikažimo:

plt.plot(x, y, 'o');

Linearna interpolacija za vrednost pri x=1.57079633/2:

y_linearna = lagrange_interpolacija(x=x[-1]/2, x_int=x[1:3], y_int=y[1:3])
y_linearna

np.float64(0.6830127)

Kvadratna:

y_kvadratna = lagrange_interpolacija(x=x[-1]/2, x_int=x[0:3], y_int=y[0:3])
y_kvadratna

np.float64(0.6997595236464176)

Kubična

y_kubična = lagrange_interpolacija(x=x[-1]/2, x_int=x, y_int=y)
y_kubična

np.float64(0.705889286844634)

Zgled ocene napake

Pri interpolaciji ponavadi funkcije \(f(x)\) ne poznamo in napako ocenimo s pomočjo formule:

\[ e=\frac{f^{(n)}(\xi)}{n!}\,(x-x_0)\,(x-x_1)\,\cdots\,(x-x_n). \]

Pri tem vrednost \(\xi\) ni znana; ker je v primeru linearne interpolacije (\(n=2\)) drugi odvod sinusne funkcije (\(f^{(n)}\)) med -1 in +1, velja:

\[ |e|\le\left|\frac{-1}{2!}\,(\pi/4-\pi/6)\,(\pi/4-\pi/3)\right|=\frac{1}{2}\,\frac{\pi}{12}\,\frac{\pi}{12}=\frac{\pi^2}{288}=0,034 \]

Poleg Lagrangeve metode bi si tukaj lahko pogledali še Newtonovo metodo interpolacije.

Interpolacija z uporabo scipy

Poglejmo si interpolacijo v okviru modula scipy.interpolate (dokumentacija).

Uporabili bomo funkcijo za interpoliranje tabele z zlepki, scipy.interpolate.interp1d (dokumentacija):

interp1d(x, y, kind='linear', axis=-1, copy=True, bounds_error=None, fill_value=nan, assume_sorted=False)

Podati moramo vsaj dva parametra: seznama interpolacijskih točk x in y. Privzeti parameter kind='linear' pomeni, da inteproliramo z odsekoma linearno funkcijo. interp1d vrne funkcijo f, ki jo kličemo (npr. y = f(x)) za izračun interpolirane vrednosti.

Parameter kind je lahko npr. tudi: 'zero', 'slinear', 'quadratic' in 'cubic'; takrat se uporabi interpolacijski zlepek (ang. spline) reda 0, 1, 2 oz. 3. Zlepke si bomo pogledali v naslednjem poglavju.

from scipy.interpolate import interp1d

Definirajmo tabelo podatkov:

x = np.array([ 1.        ,  2.14285714,  3.28571429,  4.42857143,  5.57142857,
        6.71428571,  7.85714286,  9.        ])

y = np.array([ 0.84147098,  0.84078711, -0.14362322, -0.95999344, -0.65316501,
        0.41787078,  0.999995  ,  0.41211849])

len(x)

8

from scipy.interpolate import interp1d

f = interp1d(x, y, kind='linear')
x_g = np.linspace(x[0], x[-1], 20*len(x)-1)
plt.plot(x, y, 'o', label='Interpolacijske točke')
plt.plot(x_g, f(x_g), '-', label='Interpolacija')
plt.legend();

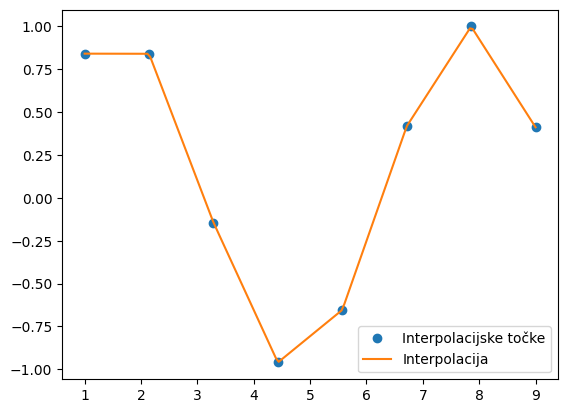
Kubični zlepki

Preden gremo v teorijo zlepkov, si poglejmo rezultat, ki ga dobimo s klicanjem funkcije interp1d s parametrom kind='cubic' (rezultat je kubični zlepek).

f = interp1d(x, y, kind='cubic')
plt.plot(x, y, 'o', label='Interpolacijske točke')
plt.plot(x_g, f(x_g), '-', label='Kubični zlepek')
plt.plot(x_g, np.sin(x_g), label='sin', alpha=0.5)
plt.legend();

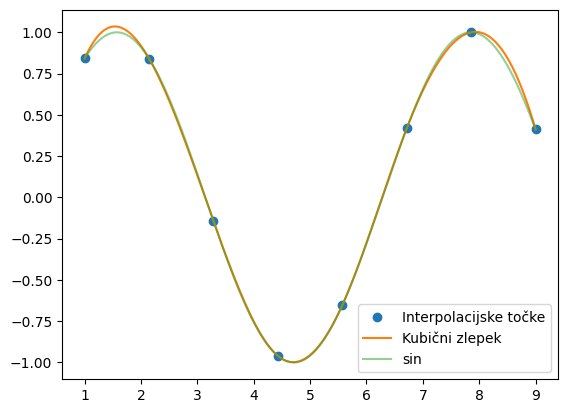
Kubični zlepki so pogost način interpolacije.

Zahtevamo, da je: \(x_0<x_1< \cdots <x_n\).

Od točke \(x_i\) do \(x_{i+1}\) naj bo zlepek polinom:

\[ f_{i,i+1}(x)= a_{i,3}\,x^3+a_{i,2}\,x^2+a_{i,1}\,x+a_{i,0}, \]

pri čemer so neznane vrednosti konstant \(a_{i,j}\).

Če imamo na primer \(n+1\) točk, potem je treba določiti \(n\) polinomov.

Celotni zlepek čez \(n+1\) točk je definiran z:

\[\begin{split} f(x) = \left\{ \begin{array}{rcl} f_{0,1}(x); && x\in[x_0, x_1)\\ f_{1,2}(x); && x\in[x_1, x_2)\\ &\vdots&\\ f_{n-1,n}(x); && x\in[x_{n-1}, x_n] \end{array} \right. \end{split}\]

Vsak polinom \(f_{i,i+1}\) je definiran s 4 konstantami \(a_{i,j}\); skupaj torej moramo izračunati \(4n\) konstant \(a_{i,j}\).

Kako določimo konstante \(a_{i,j}\)?

Za določitev \(4n\) neznak potrebujemo \(4n\) enačb. Poglejmo si, kako jih dobimo:

• \(n\) enačb dobimo iz interpolacijskega pogoja: $\(y_i=f_{i,i+1}(x_i),\quad i=0,1,2,\dots,n-1\)$

• 1 enačbo iz zadnje točke: $\(y_n=f_{n-1,n}(x_n)\)$

• \(3(n-1)\) enačb dobimo iz pogoja \(C^2\)zveznosti:

\[ \lim_{x\rightarrow x_i^-}f(x)=\lim_{x\rightarrow x_i^+}f(x), \]

\[ \lim_{x\rightarrow x_i^-}f'(x)=\lim_{x\rightarrow x_i^+}f'(x) \]

in

\[ \lim_{x\rightarrow x_i^-}f''(x)=\lim_{x\rightarrow x_i^+}f''(x). \]

Skupaj imamo definiranih \(4n-2\) enačbi, manjkata torej še dve!

Različni tipi zlepkov se ločijo po tem, kako ti dve enačbi določimo. V nadaljevanju si bomo pogledali naravne kubične zlepke.

Naravni kubični zlepki

Naravni kubični zlepki temeljijo na ideji Eulerjevega nosilca:

\[ E\,I\,\frac{\textrm{d}^4y}{\textrm{d}x^4}=q(x), \]

kjer je \(E\) elastični modul, \(I\) drugi moment preseka in \(q(x)\) zunanja porazdeljena sila. Ker zunanje porazdeljene sile ni (\(q(x)=0\)), velja:

\[ E\,I\,\frac{\textrm{d}^4y}{\textrm{d}x^4}=0. \]

Sledi, da lahko v vsaki točki tanek nosilec popišemo s polinomom tretje stopnje.

\(C^2\) zveznost je zagotovljena v kolikor so vmesne podpore nosilca členki (moment zato nima nezvezne spremembe).

Manjkajoči 2 neznanki pri naravnih kubičnih zlepkih določimo iz pogoja, da je moment na koncih enak nič (členkasto vpetje):

\[ f''(x_{0})=0\qquad\textrm{in}\qquad f''(x_{n})=0 \]

Izpeljava je natančneje prikazana v knjigi Kiusalaas J: Numerical Methods in Engineering with Python 3, 2013, stran 120 (glejte tudi J. Petrišič: Interpolacija, Fakulteta za strojništvo, 1999); podrobna izpeljava presega namen te knjige.

Tukaj si bomo pogledali samo končni rezultat, ki ga lahko izpeljemo ob zgornjih pogojih. V primeru ekvidistantne delitve \(h=x_{i+1}-x_i\) tako izpeljemo sistem enačb (\(i=1,\dots,n-1\)):

\[ k_{i-1} + 4 k_{i} + k_{i+1} = \frac{6}{h^2} \left(y_{i-1} -2 y_{i} +y_{i+1} \right). \]

kjer je neznanka \(k_i\) drugi odvod odsekovne funkcije \(k_i = f''_{i,i+1}(x_i)\).

Rešljiv sistem enačb dobimo, če dodamo še robna pogoja za naravne kubične zlepke:

\[ k_0=k_n=0. \]

Ko določimo neznake \(k_i\), jih uporabimo v odsekoma definirani funkciji:

\[ f_{i,i+1}(x)=\frac{k_i}{6}\left(\frac{(x-x_{i+1})^3}{h}-(x-x_{i+1})\,h\right) -\frac{k_{i+1}}{6}\left(\frac{(x-x_{i})^3}{h}-(x-x_{i})\,h\right) +\frac{y_i\,(x-x_{i+1})-y_{i+1}\,(x-x_{i})}{h}. \]

Numerična implementacija

Najprej pripravimo funkcijo, katera za podane interpolacijske točke reši sistem linearnih enačb in vrne koeficiente \(k_i\):

def kubicni_zlepki_koeficient(x, y):
    """ Vrne koeficiente kubičnih zlepkov `k`, matriko koeficientov `A` in konstant.
    
    x in y predstavljata seznam znanih vrednosti; x mora biti ekvidistanten.
    """
    n = len(x)
    A = np.zeros((n, n)) # pripravimo matriko koeficientov
    h = x[1]-x[0] # korak h
    for i in range(n):
        if i==0 or i==n-1:
            A[i,i] = 1. # k_0 in k_n sta nič zato tukaj damo 1
                       # pri vektorju konstant pa bomo dali 0, k_0 in k_n bosta torej 0
        else:
            A[i, i-1:i+2] = np.asarray([1., 4., 1.])
    b = np.zeros(n)
    b[1:-1] = (6/h**2)*(y[:-2] - 2*y[1:-1] + y[2:]) # desna stran zgornje enačbe
    k = np.linalg.solve(A,b)
    return k, A, b

Opomba: pri zgornjem linearnem problemu, lahko izračun zelo pohitrimo, če upoštevamo tridiagonalnost matrike koeficientov! (Glejte odgovor na stackoverflow.com).

Poglejmo si primer izračuna koeficientov:

x = np.asarray([1, 2, 3, 4, 5])
y = np.asarray([0, 1, 0, 1, 0])

k, A, b = kubicni_zlepki_koeficient(x, y)
print('Matrika koeficientov A lin. sistema:\n', A)
print('Vektor konstant b lin. sistema:     ', b)
print('Koeficienti k so:', k)

Matrika koeficientov A lin. sistema:
 [[1. 0. 0. 0. 0.]
 [1. 4. 1. 0. 0.]
 [0. 1. 4. 1. 0.]
 [0. 0. 1. 4. 1.]
 [0. 0. 0. 0. 1.]]
Vektor konstant b lin. sistema:      [  0. -12.  12. -12.   0.]
Koeficienti k so: [ 0.         -4.28571429  5.14285714 -4.28571429  0.        ]

Nato potrebujemo še kubični polinom v določenem intervalu; implementirajmo izraz:

\[ f_{i,i+1}(x)=\frac{k_i}{6}\left(\frac{(x-x_{i+1})^3}{h}-(x-x_{i+1})\,h\right) -\frac{k_{i+1}}{6}\left(\frac{(x-x_{i})^3}{h}-(x-x_{i})\,h\right) +\frac{y_i\,(x-x_{i+1})-y_{i+1}\,(x-x_{i})}{h} \]

def kubicni_zlepki(k, x, y, x_najdi):
    """ Vrne kubicni zlepek pri delitvi `xint`.
    
    :param k: koeficienti kubičnih zlepkov
    :param x in y: znane vrednosti, x mora biti ekvidistanten
    :param x_najdi: vrednosti kjer želimo izračunati kubični zlepek
    """  
    h = x[0] - x[1]
    i = int((x_najdi-x[0])//(-h))
    if i >= len(k)-1:
        i = len(k)-2
    out = ((x_najdi - x[i+1])**3/h - (x_najdi - x[i+1])*h)*k[i]/6.0 \
        - ((x_najdi - x[i])**3/h - (x_najdi - x[i])*h)*k[i+1]/6.0 \
        + (y[i]*(x_najdi - x[i+1]) \
        - y[i+1]*(x_najdi - x[i]))/h
    return out

Izračunamo interpolirane vrednosti:

xint = np.linspace(np.min(x), np.max(x), 50)
yint = np.asarray([kubicni_zlepki(k, x, y, _) for _ in xint])

plt.plot(x, y, 'o', label='Interpolacijske točke')
plt.plot(xint, yint, label='Naravni kubični zlepek')
plt.legend();

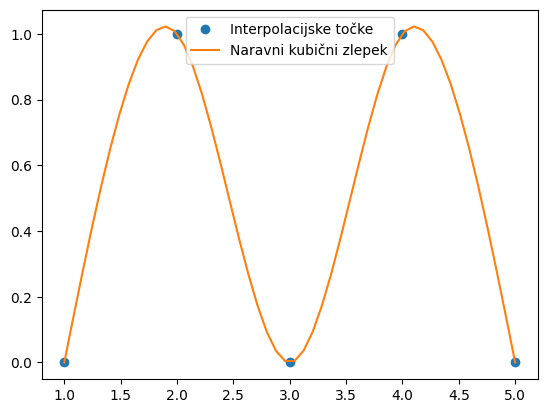
Dodatno

• 2D interpolacija: https://www.youtube.com/watch?v=_cJLVhdj0j4

• Strojno prevajanje: https://pypi.org/project/goslate)

Nekaj komentarjev modula scipy.interpolate

SciPy ima implementiranih večje število različnih interpolacij (glejte dokumentacijo). S stališča uporabe se bomo tukaj dotaknili objektne implementacije scipy.interpolate.InterpolatedUnivariateSpline (dokumentacija) (starejši pristop temelji na funkcijskem programiranju, glejte dokumentacijo scipy.interpolate.splrep):

InterpolatedUnivariateSpline(x, y, w=None, bbox=[None, None], k=3, ext=0, check_finite=False)

Pri inicializaciji objekta InterpolatedUnivariateSpline moramo posredovati interpolacijske točke x in y. Argument k s privzeto vrednostjo k=3 definira red intepolacijskega zlepka (1<=k<=5). Pomemben opcijski parameter je tudi w, ki definira uteži posameznim interpolacijskim točkam (uporabimo ga, če želimo določenim področjem dati večji poudarek).

from scipy.interpolate import InterpolatedUnivariateSpline

spl = InterpolatedUnivariateSpline(x, y, k=3) # poglejte opcije!
plt.plot(x, y, 'o', label='Interpolacijske točke')
plt.plot(xint, spl(xint), label='Kubični zlepek');
plt.plot(spl.get_knots(), spl(spl.get_knots()), 'r.', label='Vozli B-zlepkov')
plt.plot(xint, yint, label='Naravni kubični zlepki - lastna koda');
plt.legend();

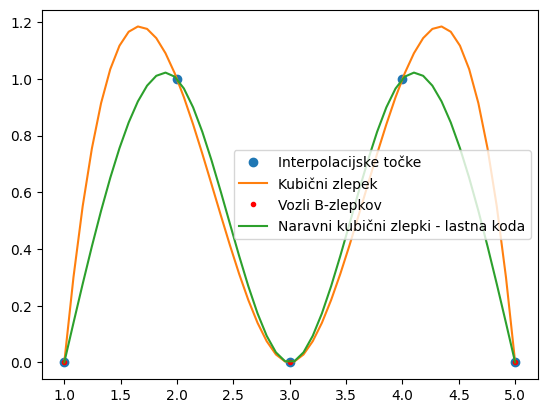
Ker gre za B-zlepke, je rezultat drugačen kot tisti, ki smo ga izpeljali z naravnimi kubičnimi zlepki. V nasprotju z naravnimi kubičnimi zlepki, ki imajo vozle (angl. knots) v interpolacijskih točkah, se vozli B-zlepkov prilagodijo podatkom. V konkretnem primeru so vozli v točkah:

spl.get_knots()

array([1., 3., 5.])

Odvajanje, integriranje … zlepkov

Zlepke lahko odvajamo in integriramo, saj so polinomi. Objekt InterpolatedUnivariateSpline je tako že pripravljen za odvajanje, integriranje, iskanje korenov (ničel), vozlov … (glejte dokumentacijo).

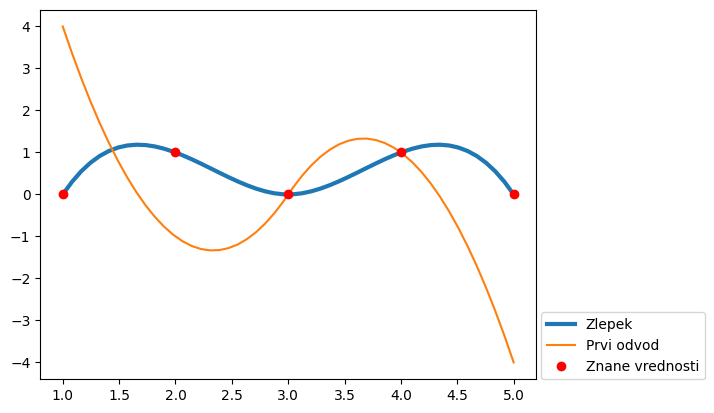
Za prvi odvod zlepka v objektu spl na primer uporabimo metodo spl.derivative(1), ki vrne nov objekt zlepka (njen red je sedaj za 1 nižji):

spl1 = spl.derivative(1)
#spl2 = spl.derivative(2)
#spl3 = spl.derivative(3)
plt.plot(xint, spl(xint), lw=3, label='Zlepek')
plt.plot(xint, spl1(xint), label='Prvi odvod')
#plt.plot(xint, spl2(xint), label='Drugi odvod')
#plt.plot(xint, spl3(xint), label='Tretji odvod')
plt.plot(x, y, 'ro', label='Znane vrednosti')
#plt.plot(spl.get_knots(), spl(spl.get_knots()), 'k.', label='Vozli B-zlepka')
plt.legend(loc=(1.01, 0));

---

Vprašanja za vaje

---

Lagrangeva metoda

def lagrange_i(x, x_int, i):
    """ Vrne vrednosti i-tega Lagrangevega polinoma
    
    x: seznam vrednosti x točk, ki jih interpoliramo
    x_int: neodvisna spremenljivka (točke, pri katerih iščemo vrednosti)
    i: indeks Lagrangevega polinoma
    """
    Li = 1.0
    for j in range(len(x)):
        
        if j != i:
            Li *= (x_int-x[j]) / (x[i]-x[j])
    return Li

# Primer
x = np.linspace(0,1,4)
y = np.random.rand(len(x))
x_int = np.linspace(np.min(x), np.max(x), 50)

Vprašanje 1: Pripravite funkcijo lagrange_interpolacija, ki kot argumente sprejme numerični polji x in y koordinat znanih točk ter numerično polje x_int koordinat, pri katerih nas zanimajo interpolirane vrednosti.

Za vsako izmed znanih točk \(x_i\) naj s pomočjo funkcije lagrange_i izračuna vrednosti polinoma \(l_i\) v točkah x_int ter na koncu izračuna in vrne vrednosti y_int \(= P_n(\) x_int \()\), tako, da izračuna vsoto:

\[P_n(x_{\text{int}}) = \sum_{i=0}^{n}y_il_i(x_{\text{int}})\]

Vprašanje 2: Pripravite nabor petih točk x, enakomerno razporejenih na intervalu \(x\in[0,2 \pi]\), ter pripadajočih vrednosti y, definiranih kot:

\[y = \sin(x)\]

Za 100 točk x_int na istem intervalu izračunajte interpolacijsko krivuljo (uporabite ustrezno funkcijo iz scipy).

Na istem grafu prikažite točke (x,y), interpolacijsko krivuljo ter prave vrednosti \(y\) pri točkah x_int.

Kako bi izračunali napako pri interpolaciji v odvisnosti od vrednosti x_int? (Prave vrednosti \(y\) poznamo!)

---

Kubični zlepki

# Primer
x = np.linspace(0,1,10)
y = np.random.rand(len(x)) - 0.5
x_int = np.linspace(x[0], x[-1], 100)

Primerjava InterpolatedUnivariateSpline in interp1d:

plt.plot(x, y, 'ro')
plt.plot(x_int, interp1d(x, y)(x_int))
plt.plot(x_int, InterpolatedUnivariateSpline(x, y)(x_int))

[<matplotlib.lines.Line2D at 0x17039e8f0e0>]

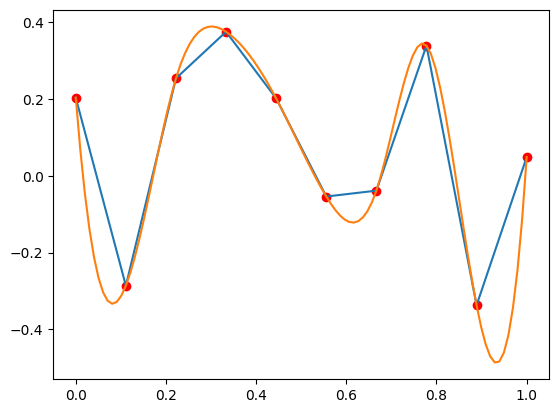
Vprašanje 3: Z uporabo poljubne scipy funkcije pripravite grafični prikaz interpolacije pripravljenih točk (x, y) z linearnimi, kvadratnimi in kubičnimi zlepki.

Vprašanje 4: Za točke x, y primerjajte interpolacijsko krivuljo kubičnih zlepkov scipy.InterpolatedUnivariateSpline z rezultatom Lagrangeve interpolacije.

Vprašanje 5: Za krivuljo kubičnih interpolacijskih zlepkov, dobljenih pri prejšnji nalogi z uprabo scipy funkcije poiščite ničle.

Rezultate grafično prikažite.

Vprašanje 6: Grafično prikažite krivuljo zlepkov iz prejšnje naloge in njene odvode.

Vprašanje 7: Podane točke (t, a) predstavljajo izmerjen potek pospeškov avtomobila v smeri vožnje. Z uporabo scipy.InterpolatedUnivariateSpline določite interpolacijsko krivuljo z zlepki 2. reda pri časih t_int.

Uporabite obstoječo funkcijo in določite ter grafično prikažite tudi krivulji hitrosti in opravljene poti (namig: help(InterpolatedUnivariateSpline)).

# Podatki
t = np.array([0, 1, 2, 3, 4, 5])
a = np.array([5, 3, 0, 0, -4, -3])
t_int = np.linspace(t[0], t[-1], 50)