# Numpy, matplotlib
Osnove modula numpy#
Kakor je omenjeno zgoraj, lahko modul numpy namestimo z upravljalnikom paketov pip z naslednjim ukazom (v kolikok ga še nimamo nameščenega):
pip install numpy
oz. paket posodobimo na najnovešo različico:
pip install numpy --upgrade
Najprej uvozimo modul (uveljavljeno je, da ga uvozimo v kratki obliki np):
import numpy as np
Gre za enega najbolj pomembnih modulov. Na kratko: gre za visoko optimiran modul za numerične izračune; zelo dobri tutoriali so zbrani na naslovu: github.com/numpy/numpy-tutorials. Za odličen uvod v Numpy si lahko ogledate YouTube posnetek: NumPy Tutorial (2021): For Physicists, Engineers, and Mathematicians
Poglejmo si najprej sintakso za vektor ničel (dokumentacija):
numpy.zeros(shape, dtype=float, order='C')
argumenti so:
shapedefinira obliko (lahko večdimenzijsko numerično polje),dtypedefinira tip podatka,orderdefinira vrstni red (lahko je C ali F kot Fortran).
Poglejmo primer:
np.zeros((3,4))
array([[0., 0., 0., 0.],
[0., 0., 0., 0.],
[0., 0., 0., 0.]])
ali pa:
np.zeros((3,5))
array([[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.]])
Podobno kot zeros se obnaša ones, vendar je namesto ničel vrednost 1 (dokumentacija).
Poglejmo si primer, kjer definiramo tudi tip int (privzeti tip je float):
np.ones(4, dtype=int)
array([1, 1, 1, 1])
Pogosto bomo tudi uporabljali razpon vrednosti arange (dokumentacija):
numpy.arange([start, ]stop, [step, ]dtype=None)
kjer so argumenti:
startzačetna vrednost razpona (privzeto 0),stopkončna vrednost razpona,stepkorak indtypetip vrednosti (če tip ni podan, se vzame tip ostalih argumetnov, npr.step).
Poglejmo primer razpona od 0 do 9 (kakor vedno pri Pythonu od je vključen, do pa ni):
np.arange(9)
array([0, 1, 2, 3, 4, 5, 6, 7, 8])
ali pa od 7 do 12 po koraku 2, vendar število s plavajočo vejico:
np.arange(7, 12, 2, dtype=float)
array([ 7., 9., 11.])
Še eno funkcijo bomo pogosto uporabili, to je linspace (dokumentacija):
numpy.linspace(start, stop, num=50, endpoint=True, retstep=False, dtype=None)
ki definiranemu razponu vrne numerično polje vrednosti na enaki razdalji (ekvidistanten razmik).
Argumenti so:
startzačetna vrednost razpona,stopkončna vrednost razpona,numštevilo točk/vozlišč,endpointali je vrednost pristopvključena ali ne,retstepv primeruTruevrne funkcija terko(rezultat, korak)dtypetip vrednosti (če tip ni podan, se vzame tip ostalih argumetnov, npr.step).
Primer generiranja 10 točk na razponu od \(-\pi\) do vključno \(+\pi\):
np.linspace(-np.pi, np.pi, 10)
array([-3.14159265, -2.44346095, -1.74532925, -1.04719755, -0.34906585,
0.34906585, 1.04719755, 1.74532925, 2.44346095, 3.14159265])
Mimogrede smo zgoraj spoznali, da ima numpy vgrajene konstante (npr. \(\pi\)):
Poglejmo še vgrajene funkcije za generiranje naključnih števil. Te najdemo v numpy.random (dokumentacija).
Najprej si poglejmo funkcijo numpy.random.seed(), ki se uporablja za ponastavitev generatorja naključnih števil (dokumentacija). To pomeni, da lahko z istim semenom (angl. seed) različni uporabniki generiramo ista naključna števila!
Spodnja vrstica:
np.random.seed(0)
bo povzročila, da bo klic generatorja naključnih števil z enakomerno porazdelitvijo numpy.random.rand() (dokumentacija) vedno rezultiral v iste vrednosti:
np.random.rand(3)
array([0.5488135 , 0.71518937, 0.60276338])
Preizkusimo ali je res, kar smo zapisali, in ponastavimo seme in kličimo generator:
np.random.seed(0)
np.random.random(3)
array([0.5488135 , 0.71518937, 0.60276338])
Zapis matrik in vektorjev#
Matrika je dimenzije m x n, kjer je na prvem mestu m število vrstic in n število stolpcev. Primer definiranja matrike dimenzije m x n = 3 x 2 je:
a = np.zeros((3, 2))
a
array([[0., 0.],
[0., 0.],
[0., 0.]])
Vektor je lahko zapisan kot vrstični vektor:
b = np.zeros(3) # (1 x 3)
b
array([0., 0., 0.])
ali kot stolpični vektor:
c = np.zeros((3, 1)) # 3 x 1
c
array([[0.],
[0.],
[0.]])
V modulu numpy lahko vektorje in matrike zapisujemo kot:
numpy.array(priporočeno, dokumentacija),numpy.matrix(dokumentacija).
Priporočena je prva oblika (numpy.array), ki pa ne sledi povsem matematičnemu zapisu (več o tem pozneje), nam pa omogoča enostavnejše programiranje in je tudi numerično bolj učinkovit pristop (vir). Pristopa numpy.matrix tukaj ne bomo obravnavali.
V angleškem jeziku bomo array prevajali kot večdimenzijsko numerično polje ali včasih večdimenzijske sezname (ker imajo nekatere podobnosti z navadnimi seznami). Nekatere knjige array tukaj prevajajo kot tabela.
Rezanje#
Rezanje (angl. slicing) seznamov smo si že pogledali v poglavju Uvod v Python. Podobno rezanje, vendar bolj splošno, velja tudi za numerična polja modula numpy.
Sintaksa rezanja (dokumentacija) je:
numpy_array[od:do:korak]
pri tem velja:
indeksiranje se začne z 0 (kot sicer pri Pythonu),
odpomeni >=,dopomeni <,od,do,korakso opcijski parametri,če parameter
odni podan, pomeni od začetka,če parameter
doni podan, pomeni do vključno zadnjega,če parameter
korakni podan, pomeni korak 1.
Primer od elementa 3 do elementa 8 po koraku 2:
b = np.arange(10)
b[3:8:2]
array([3, 5, 7])
Primer od elementa 3 naprej:
b[3:]
array([3, 4, 5, 6, 7, 8, 9])
Primer od elementa 3 naprej, vendar vsak tretji:
b[3::3]
array([3, 6, 9])
Primer zadnjih 5 elementov, vendar vsak drugi:
b[-5::2]
array([5, 7, 9])
Primer zadnjih 5 elementov brez zadnjih 2, vendar vsak drugi:
b[-5:-2:2]
array([5, 7])
Poglejmo si še rezanje večdimenzijskega numeričnega polja.#
Večdimenzijsko rezanje izvedemo tako, da dimenzije ločimo z vejico:
numpy_array[rezanje0, rezanje1,...]
kjer rezanje0 reže indeks 0 (prvo dimenzijo) v obliki od:do:korak, rezanje1 reže indeks 1 (drugo dimenzijo) in tako naprej.
Poglejmo si primer; najprej pripravimo seznam 15 števil (np.arange), nato z metodo reshape() (dokumentacija) spremenimo obliko v matriko 3 x 5:
a = np.arange(15)
a = a.reshape((3,5))
a
array([[ 0, 1, 2, 3, 4],
[ 5, 6, 7, 8, 9],
[10, 11, 12, 13, 14]])
Obliko numeričnega polja lahko preverimo z atributom shape (dokumentacija).
a.shape
(3, 5)
Atribute bomo sicer podrobno spoznali pri obravnavi razredov.
Prikažimo vrstice z indeksom 0:
a[0]
array([0, 1, 2, 3, 4])
Isti rezultat bi dobili s prikazom vrstice z indeksom 0 in vseh stolpcev:
a[0,:]
array([0, 1, 2, 3, 4])
Pogosto želimo dostopati do stoplcev, npr. stolpca z indeksom 1 (torej režemo vse vrstice in stolpec z indeksom 1):
a[:,1]
array([ 1, 6, 11])
Poglejmo si še primer rezanja prvih dveh vrstic in zadnjih dveh stolpcev:
a[:2, -2:]
array([[3, 4],
[8, 9]])
Podobna logika se uporabi pri dimenzijah višjih od 2.
Operacije nad numeričnimi polji#
Poglejmo si sedaj bolj podrobno nekatere osnovne prednosti numeričnega polja numpy.array v primerjavi z navadnim seznamom Python.
Najprej pripravimo navaden Pythonov seznam:
a = [1, 2, 3, 4, 5, 6, 7]
a
[1, 2, 3, 4, 5, 6, 7]
In nato še numerično polje numpy.array (kar iz seznama a):
b = np.array(a)
b
array([1, 2, 3, 4, 5, 6, 7])
Ko izpišemo b, smo opozorjeni, da gre za array([...]).
Poglejmo, kako se obnaša Pythonov seznam pri množenju:
2*a
[1, 2, 3, 4, 5, 6, 7, 1, 2, 3, 4, 5, 6, 7]
Opazimo, da se podvoji seznam, ne pa vrednosti, kar bi morebiti pričakovali.
Poglejmo, kako se pri množenju obnaša numerično polje numpy.array:
2*b
array([ 2, 4, 6, 8, 10, 12, 14])
Opazimo, da se podvojijo vrednosti; tako kakor bi pričakovali, ko množimo na primer skalarno vrednost in vektor!
Aritmetične operacije#
Izbor aritmetičnih operacij, ki jih numpy izvaja na nivoju posameznega elementa, je (po naraščajoči prioriteti):
x + yvsota,x - yrazlika,x * yprodukt,x / ydeljenje,x // yceloštevilsko deljenje (rezultat je celo število zaokroženo navzdol),x % yostanek pri celoštevilskem deljenju,x ** yvrnexna potencoy.
Primer:
b + 3*b - b**2
array([ 3, 4, 3, 0, -5, -12, -21])
Vse aritmetične operacije so sicer navedene v dokumentaciji in namesto kratkih oblik imamo tudi dolge, npr: numpy.power(x, y) namesto x**y; primer:
np.power(b, 2)
array([ 1, 4, 9, 16, 25, 36, 49], dtype=int32)
Mimogrede opazimo, da je rezultat tipa int32 (integer). Ko smo ustvarili ime b, smo namreč ustvarili numerično polje z elementi tipa int32.
Matematične funkcije#
numpy ponuja praktično vse potrebne matematične (in druge) operacije, navedimo jih po skupinah, kot so strukturirane v dokumentaciji:
Poglejmo primer funkcije \(\sin()\):
a = np.linspace(0, 2*np.pi, 5)
np.sin(a)
array([ 0.0000000e+00, 1.0000000e+00, 1.2246468e-16, -1.0000000e+00,
-2.4492936e-16])
Poglejmo še hitrost izvajanja:
%timeit -n100 np.sin(a)
393 ns ± 23.4 ns per loop (mean ± std. dev. of 7 runs, 100 loops each)
Podatkovni tipi#
numpy ima vnaprej definirane podatkovne tipe (statično). Celoten seznam možnih tipov je naveden v dokumentaciji.
Osredotočili se bomo predvsem na sledeče tipe:
int- celo število (poljubno veliko)float- število s plavajočo vejico (dokumentacija)complex- kompleksno število s plavajočo vejicoobject- Python objekt.
Poglejmo si nekaj primerov (cela števila, število s plavajočo vejico in kompleksna števila):
np.arange(5, dtype=int)
array([0, 1, 2, 3, 4])
np.arange(5, dtype=float)
array([0., 1., 2., 3., 4.])
np.arange(5, dtype=complex)
array([0.+0.j, 1.+0.j, 2.+0.j, 3.+0.j, 4.+0.j])
Spreminjanje elementov numeričnega polja (numpy.array)#
Podatke spreminjamo na podoben način kakor pri navadnih seznamih; v kolikor uporabljamo rezanje, moramo paziti, da so na levi in desni strani enačaja podatki iste oblike (array.shape).
Poglejmo si primer, ko matriki ničel dimenzije 3 x 4 spremenimo element z indeksom [2, 3]:
a = np.zeros((3, 4))
a[2, 3] = 100
a
array([[ 0., 0., 0., 0.],
[ 0., 0., 0., 0.],
[ 0., 0., 0., 100.]])
Sedaj spremenimo še elemente prvih dveh vrstic in prvih dveh stolpcev v vrednost 1:
a[:2, :2] = np.ones((2, 2))
a
array([[ 1., 1., 0., 0.],
[ 1., 1., 0., 0.],
[ 0., 0., 0., 100.]])
Z 2 pomnožimo stolpec z indeksom 1:
a[:,1] = 2 * a[:,1]
a
array([[ 1., 2., 0., 0.],
[ 1., 2., 0., 0.],
[ 0., 0., 0., 100.]])
Bodite pozorni na to, da na tak način naredimo pogled (view) na podatke (ne naredimo kopije podatkov).
Za primer najprej naredimo novo ime pogled:
pogled = a[:, 2]
pogled
array([0., 0., 0.])
Sedaj spremenimo izbrane vrednosti numeričnega polja a:
a[:, 2] = 5
a
array([[ 1., 2., 5., 0.],
[ 1., 2., 5., 0.],
[ 0., 0., 5., 100.]])
Vrednosti pogled nismo spreminjali. Ker pa ime kaže na isto mesto kakor a[:, 2], so vrednosti spremenjene:
pogled
array([5., 5., 5.])
Če želimo kopijo, moramo narediti tako:
kopija = a[:, 2].copy()
kopija
array([5., 5., 5.])
in rezultat kopija ostane nespremenjen:
a[:, 2] = 2
kopija
array([5., 5., 5.])
Osnove matričnega računanja#
Če želite ponoviti matematične osnove matričnega računanja, potem sledite tej povezavi (gre za kratek in dober pregled prof. dr. T. Koširja). Pogledali bomo, kako matrične račune izvedemo s pomočjo paketa numpy.
Najprej definirajmo matriki \(\mathbf{A}\) in \(\mathbf{B}\):
A = np.array([[1, 2], [3, 2]])
B = np.array([[1, 1], [2, 2]])
ter vektorja \(\mathbf{x}\) in \(\mathbf{y}\).
x = np.array([1, 2])
y = np.array([3, 4])
Skalarni produkt dveh vektorjev izvedemo s funkcijo dot() (dokumentacija):
numpy.dot(a, b, out=None)
kjer argumenta a in b predstavljata numerični polji numpy.array (poljubne dimenzije), ki jih želimo množiti. Če sta a in b dimenzije 1 se izvede skalarni produkt. Pri dimenziji 2 (matrike) se izračuna produkt matrik. Za uporabo funkcije dot() pri dimenzijah več kot 2: glejte dokumentacijo.
Poglejmo primer množenja dveh vektorjev, to lahko izvedemo tako:
np.dot(x, y)
11
ali tudi tako:
x.dot(y)
11
Zgoraj smo omenili, da numpy.array ne sledi dosledno matematičnemu zapisu. Če bi, bi namreč eden od vektorjev moral biti vrstični, drugi stolpični. numpy to poenostavi in zato je koda lažje berljiva in krajša.
Poglejmo sedaj množenje matrike z vektorjem (opazimo, da transponiranje x ni potrebno):
np.dot(A, x)
array([5, 7])
Lahko pa seveda pripravimo matematično korektno transponirano obliko vektorja (ampak vidimo, da je zapis neroden):
A.dot(np.transpose([x]))
array([[5],
[7]])
Transponiranje ima sicer tudi kratko obliko, prek atributa T, npr. za matriko \(\mathbf{A}\):
A.T
array([[1, 3],
[2, 2]])
Poglejmo si primer množenja dveh matrik:
np.dot(A, B)
array([[5, 5],
[7, 7]])
Od Pythona 3.5 naprej se za množenje matrik (in vektorjev) uporablja tudi operator @ (dokumentacija), ki omogoča kratek in pregleden zapis.
Zgornji primeri zapisani z operatorjem @:
x @ y
11
A @ x
array([5, 7])
A @ B
array([[5, 5],
[7, 7]])
Vektorski produkt izračunamo s funkcijo numpy.cross() (dokumentacija):
numpy.cross(a, b, axisa=-1, axisb=-1, axisc=-1, axis=None)
kjer a in b definirata komponente vektorjev. Če sta podani samo dve komponenti (\(x\) in \(y\)), se izračuna skalarna vrednost (komponenta \(z\)); če so podane tri komponente, je rezultat tudi vektor s tremi komponentami. Uporaba funkcije je možna tudi na večdimenzijskih numeričnih poljih in temu so namenjeni preostali argumenti (glejte dokumentacijo).
Primer vektorskega produkta ravninskih vektorjev:
x = np.array([1, 0])
y = np.array([0, 1])
np.cross(x, y)
array(1)
Primer vektorskega produkta prostorskih vektorjev:
x = np.array([1, 0, 0])
y = np.array([0, 1, 0])
np.cross(x, y)
array([0, 0, 1])
Nekatere funkcije knjižnice numpy#
Pogledali si bomo še nekatere funkcije, ki jih bolj ali manj pogosto potrebujemo.
Enotsko matriko definiramo s funkcijo numpy.identity() (dokumentacija):
numpy.identity(n, dtype=None)
kjer argument n definira število vrstic in stolpcev pravokotne matrike. Tip dtype je privzeto float.
Primer enotske matrike:
A = np.identity(3)
A
array([[1., 0., 0.],
[0., 1., 0.],
[0., 0., 1.]])
Do diagonalnih elementov matrike dostopamo s pomočjo funkcije numpy.diagonal() (dokumentacija)
numpy.diagonal(a, offset=0, axis1=0, axis2=1)
Če je matrika dvodimenzijska, potem funkcija s privzetimi argumenti vrne diagonalno os. Če je dimenzija višja od 2, se uporabi osi axis1 in axis2, da se izloči dvodimenzijsko polje, nato pa določi diagonalo glede na elemente [i, i+offset].
Poglejmo primer izločanja diagonale:
np.diagonal(A)
array([1., 1., 1.])
in uporabe offset=1 za sosednjo diagonalo (najprej pripravimo nesimetirčno matriko):
A[0, 1] = 10
np.diagonal(A, offset=1)
array([10., 0.])
Podobno sintakso kot numpy.diagonal() ima funkcija numpy.trace(), ki izračuna vsoto (sled) diagonalnih elementov (dokumentacija):
numpy.trace(a, offset=0, axis1=0, axis2=1,
dtype=None, out=None)
Primer sledi diagonale:
np.trace(A)
3.0
in potem sosednje diagonale:
np.trace(A, offset=1)
10.0
Pogosto nas zanimata največji ali najmanjši element nekega numeričnega polja. numpy je tukaj zelo splošen. Poglejmo si na primeru funkcije numpy.max() (dokumentacija):
numpy.max(a, axis=None, out=None)
Izpostavimo argument axis, ki pove, čez kateri indeks iščemo maksimalno vrednost. Če je axis=None se določi največja vrednost v celotnem polju.
Primer izračuna največje vrednosti celotnega polja (prej poglejmo A):
A
array([[ 1., 10., 0.],
[ 0., 1., 0.],
[ 0., 0., 1.]])
np.max(A, axis=1)
array([10., 1., 1.])
Primer izračuna največje vrednosti čez vrstice (torej po stolpcih):
np.max(A, axis=0)
array([ 1., 10., 1.])
Primer izračuna največje vrednosti čez stolpce (torej po vrsticah):
np.max(A, axis=1)
array([10., 1., 1.])
Par funkcije max() je numpy.argmax(), kateri določi indekse največje vrednosti.
Primer uporabe:
A
array([[ 1., 10., 0.],
[ 0., 1., 0.],
[ 0., 0., 1.]])
np.argmax(A, axis=0)
array([0, 0, 2], dtype=int64)
Linearna algebra z numpy#
Pozneje bomo linearno algebro bolj podrobno spoznali in bomo sami pisali algoritme. Tukaj si poglejmo nekatere osnove, ki so vgrajene v modul numpy.
Za primer najprej definirajmo matriko in vektor:
A = np.array([[4, -2],
[-2, 4]])
b = np.array([1, 2])
Inverzno matriko izračunamo z uporabo funkcije numpy.linalg.inv() (dokumentacija):
numpy.linalg.inv(a)
np.linalg.inv(A)
array([[0.33333333, 0.16666667],
[0.16666667, 0.33333333]])
Sistem linearnih enačb, ki ga definirata matrika koeficientov a in vektor konstant b, rešimo s pomočjo funkcije numpy.linalg.solve() (dokumentacija):
numpy.linalg.solve(a, b)
Primer:
rešitev = np.linalg.solve(A, b)
rešitev
array([0.66666667, 0.83333333])
Enakost elementov numeričnega polja a in b (znotraj določene tolerance) preverimo s funkcijo numpy.isclose() (dokumentacija):
numpy.isclose(a, b, rtol=1e-05, atol=1e-08, equal_nan=False)
Primer:
np.isclose(np.dot(A, rešitev), b)
array([ True, True])
Vektorizacija algoritmov#
V tem poglavju želimo izpostaviti vektorizacijo algoritmov. Glede na to kako Python in numpy delujeta se je potrebno izogibati zankam. Bistveno hitreje lahko izvajamo izračune, če jih uspemo vektorizirati; to pomeni, da izračune izvajamo na nivoju vektorjev (oz. numeričnih polj) in ne elementov.
Za primer si najprej pripravimo podatke (dva vektorja dolžine 1000)
N = 1000
a = np.arange(N)
b = np.arange(N)
Izračunajmo skalarni produkt vektorjev z uporabo zanke for:
c = 0
for i in range(N):
c += a[i] * b[i]
c
332833500
Izmerimo hitrost:
%%timeit -n100
c = 0
for i in range(N):
c += a[i] * b[i]
177 µs ± 3.94 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
Isti rezultat pridobimo še v vektorski obliki:
%%timeit -n100
c = a @ b
2.33 µs ± 90.2 ns per loop (mean ± std. dev. of 7 runs, 100 loops each)
Vidimo, da je vektorski način bistveno hitrejši (za še hitrejši način glejte numba v dodatku)!
Osnove modula matplotlib#
V Pythonu imamo več možnosti za prikaz rezultatov v grafični obliki. Najbolj uporabni paketi so:
matplotlibza visoko kakovostne, visoko prilagodljive slike (relativno počasno),pyqtgraphza kakovostne in prilagodljive uporabniške vmesnike (zelo hitro),bokehza interaktiven prikaz v brskalniku (relativno hitro).
Obstaja še veliko drugih; dober pregled je naredil Jake VanderPlas na konferenci PyCon 2017 (sicer avtor paketa za deklerativno vizualizacijo: Altair).
Osnovna uporaba#
Najbolj razširjen in najbolj splošno uporabljen je paket matplotlib:
Sposobnosti paketa najbolje prikazuje galerija. Gre za zelo sofisticiran paket in tukaj si bomo na podlagi primerov pogledali nekatere osnove.
Pri uporabi vam lahko koristi plonk listek:
Tipično uvozimo matplotlib.pyplot kot plt:
import matplotlib.pyplot as plt
Znotraj Jupyter notebooka obstajata dva načina prikaza slike (v oglatem oklepaju je magic ukaz za proženje):
[%matplotlib inline]: slike so vključene v notebook (medvrstični način),[%matplotlib widget]: slike so interaktivno vključene v notebook (medvrstični interaktivni način), zahteva namestitev paketa ipympl,[%matplotlib notebook]: slike so interaktivno vključene v notebook (medvrstični interaktivni način).
Opomba: interaktivni način se v pasivni, spletni/pdf verziji te knjige ne prikaže pravilno.
Tukaj bomo najpogosteje uporabljali medvrstični način:
%matplotlib inline
Kratek primer:
t = np.linspace(1, 130, 44000)
žvižg = np.sin(t**2)
plt.plot(t, žvižg, label='Žvižg')
plt.xlim(1, 10)
plt.title('Žvižg: $t^2$ (podpora za LaTeX: $\\sqrt{\\frac{a}{b}}$)')
plt.legend();
plt.show()
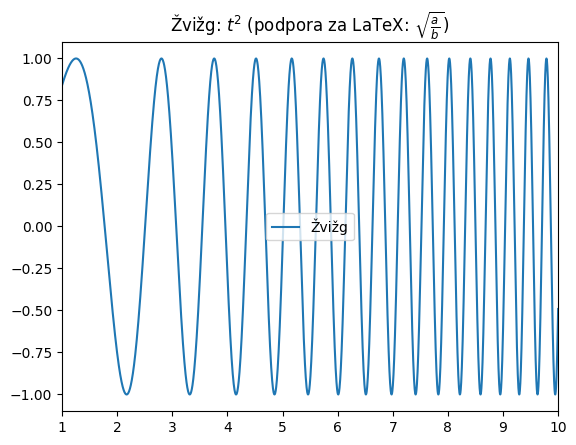
Mimogrede, zakaj to imenujemo žvižg (oz. kvadraten žvižg)? Da dobimo odgovor, podatke predvajamo na zvočnik:
from IPython.display import Audio, display
display(Audio(data=žvižg, rate=44000))
Aktivirajmo sedaj interaktivni način (glejte tudi %matplotlib):
%matplotlib notebook
%matplotlib notebook
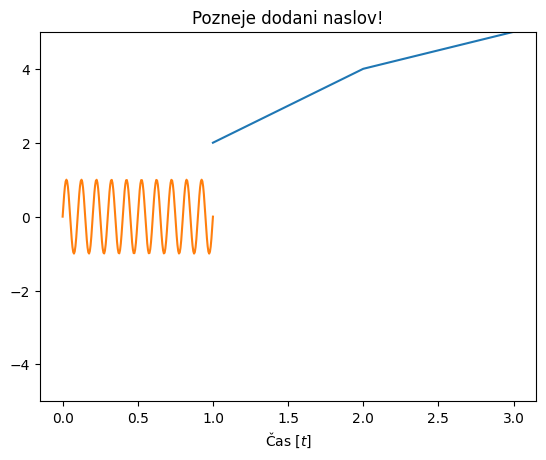
plt.plot([1,2,3], [2,4,5]);
Zgornjo sliko lahko sedaj interaktivno klikamo in tudi dopolnjujemo s kodo:
plt.title('Pozneje dodani naslov!')
plt.xlabel('Čas [$t$]');
Interaktivna uporaba#
Pri tem predmetu bomo večkrat uporabljali interaktivnost pri delu z grafičnimi prikazi. V ta namen najprej uvozimo interact iz paketa ipywidgets:
from ipywidgets import interact
Potem definiramo sliko kot funkcijo z argumenti amplituda, fr, faza in dušenje:
def slika(amplituda=1, fr=10, faza=0, dušenje=0.):
t = np.linspace(0, 1, 200)
f = amplituda * np.sin(2*np.pi*fr*t - faza) * np.exp(-dušenje*2*np.pi*fr*t)
plt.plot(t, f)
plt.ylim(-5, 5)
plt.show()
Gremo nazaj na medvrstično uporabo in kličemo funkcijo za izris slike (privzeti argumenti):
%matplotlib inline
slika()
Če funkcijo za izris slike pošljemo v funkcijo interact, slednja poskrbi za interaktivne gumbe, s katerimi lahko spreminajmo parametre klicanja funkcije slika:
interact(slika);
Razpon parametov lahko tudi sami definiramo:
interact(slika, amplituda=(1, 5, 1), dušenje=(0, 1, 0.05), fr=(10, 100, 1), faza=(0, 2*np.pi, np.pi/180));
Napredna uporaba#
Prikaz več funkcij#
Poglejmo si preprost primer prikaza več funkcij (najprej, opcijsko, definirajmo fonte za izpis v pdf):
from matplotlib import rc
rc('font',**{'family':'serif'})
plt.rcParams['pdf.fonttype'] = 42
x = np.linspace(0, 10, 100)
y1 = np.sin(x)
y2 = np.sin(x+1)
y3 = np.sin(x**1.2)
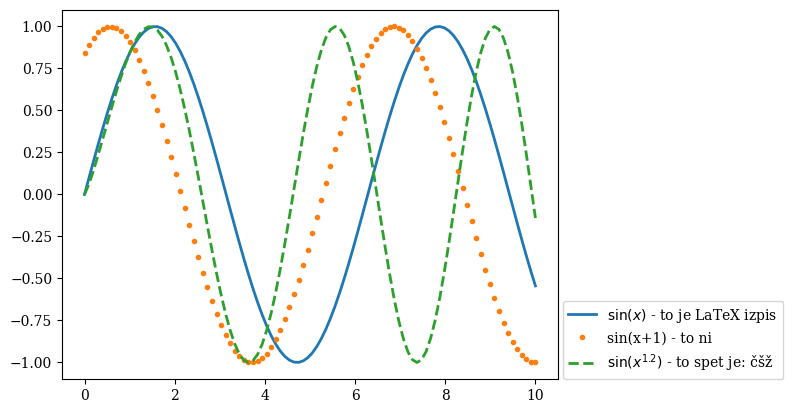
plt.plot(x, y1, '-', label='$\sin(x)$ - to je LaTeX izpis', linewidth = 2);
plt.plot(x, y2, '.', label='sin(x+1) - to ni', linewidth = 2);
plt.plot(x, y3, '--', label='$\sin(x^{1.2})$ - to spet je: čšž', linewidth = 2);
plt.legend(loc=(1.01,0));
plt.savefig('data/prvi plot.pdf')
Prikaz več slik#
Več slik prikažemo s pomočjo metode subplot, ki definira mrežo in lego naslednjega izrisala.
plt.subplot(2, 2, 1)
plt.plot(x, y1, 'r')
plt.subplot(2, 2, 2)
plt.plot(x, y2, 'g')
V primeru zgoraj plt.subplot(2, 2, 1) pomeni: mreža naj bo 2 x 2, riši v sliko 1 (levo zgoraj). Naslednjič se kliče plt.subplot(2, 2, 2) kar pomeni mreža 2 x 2, riši v sliko 2 (desno zgoraj) in tako naprej. Opazimo, da se indeks slik začne z 1; lahko bi rekli, da gre za nekonsistentnost v Pythonu, razlog pa je v tem, da je bil matplotlib rojen v ideji, da bi uporabnikom Pythona uporabil čimbolj podoben način izrisa, kakor so ga poznali v Matlabu (kjer se indeks začne z 1).
Delujoči primer je:
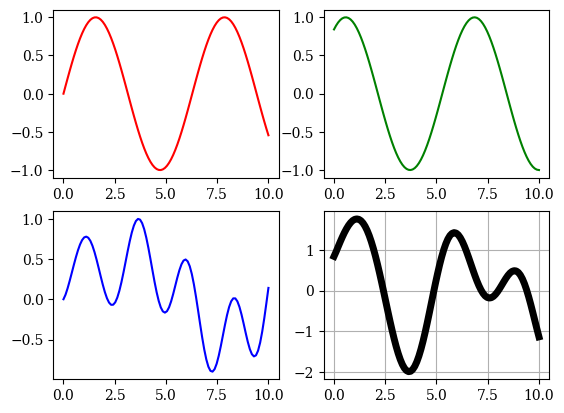
plt.subplot(2, 2, 1)
plt.plot(x, y1, 'r')
plt.subplot(2, 2, 2)
plt.plot(x, y2, 'g')
plt.subplot(2, 2, 3)
plt.plot(x, y2*y3, 'b')
plt.subplot(2, 2, 4)
plt.plot(x, y2+y3, 'k', linewidth=5);
plt.grid()
Histogram#
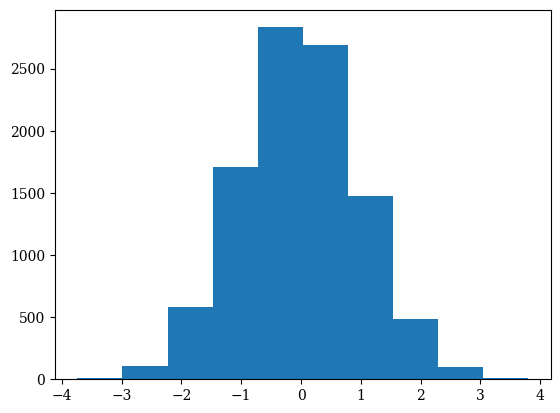
Generirajmo 10000 normalno porazdeljenih vzorcev in jih prikažimo v obliki histograma:
np.random.seed(0)
x = np.random.normal(size=10000)
plt.hist(x);
Uporaba primerov iz matplotlib.org#
Primere iz galerije lahko uvozimo s pomočjo magične funkcije %load.
Poskusite:
%load http://matplotlib.org/mpl_examples/lines_bars_and_markers/fill_demo.py%load http://matplotlib.org/examples/widgets/slider_demo.py
Nekaj vprašanj za razmislek!#
Naredite slovar lokalno nameščenih modulov (uporabite izpeljevanje slovarjev, ključ naj bo ime modula, vrednost naj bo verzija).
S pomočjo slovarja iz prejšnje točke čimbolj preprosto preverite, ali so nameščeni sledeči moduli: [‚numpy‘, ‚scipy‘, ‚matplotlib‘, ‚pandas‘, ‚pyjamas‘, ‚openpyxl‘].
Namestite poljubni modul iz https://pypi.org in ga preizkusite.
Pretvorite navaden Pythonov seznam v
numpynumerično polje. Preverite tip enega in drugega.Raziščite funkcije
np.ones,np.zeros_like,np.arange,np.linspace(ali zadnja funkcija lahko vrne korak?).Prikažite uporabo rezanja.
Prikažite razliko med vrstičnim in stolpičnim vektorjem. Prikažite tipične matematične operacije med vektorji in matrikami.
Ustvarite matriko ničel dimenzije 3 x 2 in drugi stolpec zapolnite z vektorjem enic.
Ustvarite enotsko matriko dimenzije 5 podatkovnega tipa
complex.Ustvarite enotsko matriko dimenzije
Nin izračunajte vsoto poljubnga stolpca. Poskusite najti najhitrejši (vektoriziran) način in ga primerjajte s pristopom v zanki. Namig: np.sum().V matriki iz prejšnje točke zamenjajte poljubna stolpca, nato še poljubni vrstici. Preverite hitrost vaše implementacije.
S pomočjo funkcije
np.random.randustvarite dvorazsežno matriko poljubne dimenzije in najdite največjo in najmanjšo vrednost. Preverite možnostaxisv funkcijinp.maxalinp.min.V matriki iz prejšnje točke najdite indeks, kjer se nahaja največja vrednost.
Na primeru preprostega diagrama prikažite razliko med inline in interaktivno uporabo knjižnice
matplotlib.Na primeru preprostega diagrama prikažite uporabo vsaj 5 različnih tipov črte in 5 različnih barv.
Raziščite primere http://matplotlib.org/gallery.html. Za primer si podrobneje poglejte enega od zgledov na temo zaznamb annotation. Izbrani primer namestite na vaš računalnik.
Na primeru preprostega diagrama prikažite uporabo zaznamb.
Dodatno: Naredite preprosto animacijo.
Dodatno: Izrišite več krogov naključne lege in velikosti ter poljubne barve. Ob kliku se krogom naj spremeni barva.
Dodatno#
numba#
Paket numba se v zadnjem obdobju zelo razvija in lahko numerično izvajanje še dodatno pohitri (tudi v povezavi z grafičnimi karticami oz. GPU procesorji).
Za zgled tukaj uporabimo jit (just-in-time compilation) iz paketa numba:
from numba import jit
jit uporabimo kot dekorator funkcije, ki jo želimo pohitriti:
@jit
def skalarni_produkt(a, b):
c = 0
for i in range(N):
c += a[i] * b[i]
return c
C:\Users\janko\AppData\Local\Temp\ipykernel_19024\2600651875.py:1: NumbaDeprecationWarning: The 'nopython' keyword argument was not supplied to the 'numba.jit' decorator. The implicit default value for this argument is currently False, but it will be changed to True in Numba 0.59.0. See https://numba.readthedocs.io/en/stable/reference/deprecation.html#deprecation-of-object-mode-fall-back-behaviour-when-using-jit for details.
@jit
Sedaj definirajmo vektorja:
N = 1000
a = np.arange(N)
b = np.arange(N)
Preverimo hitrost numpy skalarnega produkta:
%%timeit -n1000
a @ b
2.66 µs ± 412 ns per loop (mean ± std. dev. of 7 runs, 1,000 loops each)
Preverimo še hitrost numba pohitrene verzije. Prvi klic izvedemo, da se izvede kompilacija, potem merimo čas:
skalarni_produkt(a, b)
332833500
%%timeit -n1000
skalarni_produkt(a, b)
449 ns ± 10.8 ns per loop (mean ± std. dev. of 7 runs, 1,000 loops each)
Vidimo, da smo še izboljšali hitrost!
matplotlib: animacije, povratni klic, XKCD stil#
Z matplotlib lahko pripravimo tudi animacije. Dva primera lahko najdete tukaj:
Več v dokumentaciji.
Slika s povratnim klicem (angl. call back):
Pripravite lahko tudi na roko narisane slike (XKCD stil):
Za najbolj zagrete#
Naučite se še kaj novega na chrisalbon.com.