Numerično integriranje

Uvod

V okviru tega poglavja bomo za dano funkcijo \(f(x)\) izračunali določen integral:

\[\int_a^b\,f(x)\,\textrm{d}x\]

kjer sta \(a\) in \(b\) meji integriranja, \(f(x)\) pa so vrednosti funkcije, ki jih pridobimo iz tabele vrednosti ali s pomočjo analitične funkcije.

Pri numeričnem integriranju integral ocenimo z \(I\) in velja

\[\int_a^b\,f(x)\,\textrm{d}x= I + E,\]

kjer je \(E\) napaka ocene integrala.

Numerični integral bomo računali na podlagi diskretne vsote:

\[I=\sum_{i=0}^{m}A_i\,f(x_i),\]

kjer so \(A_i\) uteži, \(x_i\) pa vozlišča na intervalu \([a, b]\) in je \(m+1\) število vozlišč.

Ogledali si bomo dva različna pristopa k numerični integraciji:

1. Newton-Cotesov pristop, ki temelji na ekvidistantnih vozliščih (konstanten korak integracije) in

2. Gaussov integracijski pristop, kjer so vozlišča postavljena tako, da se doseže natančnost za polinome.

Motivacijski primer

Pri numeričnem integriranju si bomo pomagali s konkretnim primerom:

\[\int_1^2 x\,\sin(x)\,\textrm{d}x\]

Pripravimo si vozlišča. Osnovni korak naj bo \(h=0.25\), v tem primeru imamo štiri podintervale in pet vozlišč, pri koraku \(2h\) so tri vozliščne točke in pri koraku \(4h\) samo dve (skrajni):

import numpy as np
xg, hg = np.linspace(1, 2, 100, retstep=True) # goste točke (za prikaz)
x2v, h2v = np.linspace(1, 2, 2, retstep=True)  # korak h2v = 1 (2 vozlišči)
x3v, h3v = np.linspace(1, 2, 3, retstep=True)  # korak h3v = 0.5 (3 vozlišča)
x4v, h4v = np.linspace(1, 2, 4, retstep=True)  # korak h4v = 0.33.. (4 vozlišča)
x5v, h5v = np.linspace(1, 2, 5, retstep=True)  # korak h5v = 0.25 (5 vozlišč)

Pripravimo še funkcijske vrednosti:

yg = xg * np.sin(xg)
y2v = x2v * np.sin(x2v)
y3v = x3v * np.sin(x3v)
y4v = x4v * np.sin(x4v)
y5v = x5v * np.sin(x5v)

Pripravimo prikaz podatkov:

import matplotlib.pyplot as plt
from matplotlib import rc # to uvozimo, da so fonti na sliki latex ustrezni
#rc('font',**{'family':'sans-serif','sans-serif':['Helvetica']})
rc('text', usetex=True)
%matplotlib inline
def fig_motivacija():
    plt.fill_between(xg, yg, alpha=0.25, facecolor='r')
    plt.annotate(r'$\int_1^2\,x\,\sin(x)\,\textrm{d}x$', (1.3, 0.5), fontsize=22)
    plt.plot(xg, yg, lw=3, alpha=0.5, label=r'$x\,\sin(x)$')
    plt.plot(x2v, y2v, 's', alpha=0.5, label=f'$h={h2v}$', markersize=14)
    plt.plot(x3v, y3v, 'o', alpha=0.5, label=f'$h={h3v}$', markersize=10)
    plt.legend(loc=(1.01, 0))
    plt.ylim(0, 2)
    plt.show()

Prikažimo podatke:

fig_motivacija()

---------------------------------------------------------------------------
FileNotFoundError                         Traceback (most recent call last)
File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/texmanager.py:250, in TexManager._run_checked_subprocess(cls, command, tex, cwd)
    249 try:
--> 250     report = subprocess.check_output(
    251         command, cwd=cwd if cwd is not None else cls._texcache,
    252         stderr=subprocess.STDOUT)
    253 except FileNotFoundError as exc:

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/subprocess.py:466, in check_output(timeout, *popenargs, **kwargs)
    464     kwargs['input'] = empty
--> 466 return run(*popenargs, stdout=PIPE, timeout=timeout, check=True,
    467            **kwargs).stdout

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/subprocess.py:548, in run(input, capture_output, timeout, check, *popenargs, **kwargs)
    546     kwargs['stderr'] = PIPE
--> 548 with Popen(*popenargs, **kwargs) as process:
    549     try:

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/subprocess.py:1026, in Popen.__init__(self, args, bufsize, executable, stdin, stdout, stderr, preexec_fn, close_fds, shell, cwd, env, universal_newlines, startupinfo, creationflags, restore_signals, start_new_session, pass_fds, user, group, extra_groups, encoding, errors, text, umask, pipesize, process_group)
   1023             self.stderr = io.TextIOWrapper(self.stderr,
   1024                     encoding=encoding, errors=errors)
-> 1026     self._execute_child(args, executable, preexec_fn, close_fds,
   1027                         pass_fds, cwd, env,
   1028                         startupinfo, creationflags, shell,
   1029                         p2cread, p2cwrite,
   1030                         c2pread, c2pwrite,
   1031                         errread, errwrite,
   1032                         restore_signals,
   1033                         gid, gids, uid, umask,
   1034                         start_new_session, process_group)
   1035 except:
   1036     # Cleanup if the child failed starting.

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/subprocess.py:1955, in Popen._execute_child(self, args, executable, preexec_fn, close_fds, pass_fds, cwd, env, startupinfo, creationflags, shell, p2cread, p2cwrite, c2pread, c2pwrite, errread, errwrite, restore_signals, gid, gids, uid, umask, start_new_session, process_group)
   1954 if err_filename is not None:
-> 1955     raise child_exception_type(errno_num, err_msg, err_filename)
   1956 else:

FileNotFoundError: [Errno 2] No such file or directory: 'latex'

The above exception was the direct cause of the following exception:

RuntimeError                              Traceback (most recent call last)
File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/backend_bases.py:2157, in FigureCanvasBase.print_figure(self, filename, dpi, facecolor, edgecolor, orientation, format, bbox_inches, pad_inches, bbox_extra_artists, backend, **kwargs)
   2154     # we do this instead of `self.figure.draw_without_rendering`
   2155     # so that we can inject the orientation
   2156     with getattr(renderer, "_draw_disabled", nullcontext)():
-> 2157         self.figure.draw(renderer)
   2158 if bbox_inches:
   2159     if bbox_inches == "tight":

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/artist.py:94, in _finalize_rasterization.<locals>.draw_wrapper(artist, renderer, *args, **kwargs)
     92 @wraps(draw)
     93 def draw_wrapper(artist, renderer, *args, **kwargs):
---> 94     result = draw(artist, renderer, *args, **kwargs)
     95     if renderer._rasterizing:
     96         renderer.stop_rasterizing()

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/artist.py:71, in allow_rasterization.<locals>.draw_wrapper(artist, renderer)
     68     if artist.get_agg_filter() is not None:
     69         renderer.start_filter()
---> 71     return draw(artist, renderer)
     72 finally:
     73     if artist.get_agg_filter() is not None:

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/figure.py:3264, in Figure.draw(self, renderer)
   3261             # ValueError can occur when resizing a window.
   3263     self.patch.draw(renderer)
-> 3264     mimage._draw_list_compositing_images(
   3265         renderer, self, artists, self.suppressComposite)
   3267     renderer.close_group('figure')
   3268 finally:

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/image.py:134, in _draw_list_compositing_images(renderer, parent, artists, suppress_composite)
    132 if not_composite or not has_images:
    133     for a in artists:
--> 134         a.draw(renderer)
    135 else:
    136     # Composite any adjacent images together
    137     image_group = []

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/artist.py:71, in allow_rasterization.<locals>.draw_wrapper(artist, renderer)
     68     if artist.get_agg_filter() is not None:
     69         renderer.start_filter()
---> 71     return draw(artist, renderer)
     72 finally:
     73     if artist.get_agg_filter() is not None:

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/axes/_base.py:3226, in _AxesBase.draw(self, renderer)
   3223 if artists_rasterized:
   3224     _draw_rasterized(self.get_figure(root=True), artists_rasterized, renderer)
-> 3226 mimage._draw_list_compositing_images(
   3227     renderer, self, artists, self.get_figure(root=True).suppressComposite)
   3229 renderer.close_group('axes')
   3230 self.stale = False

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/image.py:134, in _draw_list_compositing_images(renderer, parent, artists, suppress_composite)
    132 if not_composite or not has_images:
    133     for a in artists:
--> 134         a.draw(renderer)
    135 else:
    136     # Composite any adjacent images together
    137     image_group = []

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/artist.py:71, in allow_rasterization.<locals>.draw_wrapper(artist, renderer)
     68     if artist.get_agg_filter() is not None:
     69         renderer.start_filter()
---> 71     return draw(artist, renderer)
     72 finally:
     73     if artist.get_agg_filter() is not None:

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/axis.py:1405, in Axis.draw(self, renderer)
   1402 renderer.open_group(__name__, gid=self.get_gid())
   1404 ticks_to_draw = self._update_ticks()
-> 1405 tlb1, tlb2 = self._get_ticklabel_bboxes(ticks_to_draw, renderer)
   1407 for tick in ticks_to_draw:
   1408     tick.draw(renderer)

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/axis.py:1332, in Axis._get_ticklabel_bboxes(self, ticks, renderer)
   1330 if renderer is None:
   1331     renderer = self.get_figure(root=True)._get_renderer()
-> 1332 return ([tick.label1.get_window_extent(renderer)
   1333          for tick in ticks if tick.label1.get_visible()],
   1334         [tick.label2.get_window_extent(renderer)
   1335          for tick in ticks if tick.label2.get_visible()])

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/axis.py:1332, in <listcomp>(.0)
   1330 if renderer is None:
   1331     renderer = self.get_figure(root=True)._get_renderer()
-> 1332 return ([tick.label1.get_window_extent(renderer)
   1333          for tick in ticks if tick.label1.get_visible()],
   1334         [tick.label2.get_window_extent(renderer)
   1335          for tick in ticks if tick.label2.get_visible()])

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/text.py:969, in Text.get_window_extent(self, renderer, dpi)
    964     raise RuntimeError(
    965         "Cannot get window extent of text w/o renderer. You likely "
    966         "want to call 'figure.draw_without_rendering()' first.")
    968 with cbook._setattr_cm(fig, dpi=dpi):
--> 969     bbox, info, descent = self._get_layout(self._renderer)
    970     x, y = self.get_unitless_position()
    971     x, y = self.get_transform().transform((x, y))

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/text.py:373, in Text._get_layout(self, renderer)
    370 ys = []
    372 # Full vertical extent of font, including ascenders and descenders:
--> 373 _, lp_h, lp_d = _get_text_metrics_with_cache(
    374     renderer, "lp", self._fontproperties,
    375     ismath="TeX" if self.get_usetex() else False,
    376     dpi=self.get_figure(root=True).dpi)
    377 min_dy = (lp_h - lp_d) * self._linespacing
    379 for i, line in enumerate(lines):

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/text.py:69, in _get_text_metrics_with_cache(renderer, text, fontprop, ismath, dpi)
     66 """Call ``renderer.get_text_width_height_descent``, caching the results."""
     67 # Cached based on a copy of fontprop so that later in-place mutations of
     68 # the passed-in argument do not mess up the cache.
---> 69 return _get_text_metrics_with_cache_impl(
     70     weakref.ref(renderer), text, fontprop.copy(), ismath, dpi)

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/text.py:77, in _get_text_metrics_with_cache_impl(renderer_ref, text, fontprop, ismath, dpi)
     73 @functools.lru_cache(4096)
     74 def _get_text_metrics_with_cache_impl(
     75         renderer_ref, text, fontprop, ismath, dpi):
     76     # dpi is unused, but participates in cache invalidation (via the renderer).
---> 77     return renderer_ref().get_text_width_height_descent(text, fontprop, ismath)

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/backends/backend_agg.py:211, in RendererAgg.get_text_width_height_descent(self, s, prop, ismath)
    209 _api.check_in_list(["TeX", True, False], ismath=ismath)
    210 if ismath == "TeX":
--> 211     return super().get_text_width_height_descent(s, prop, ismath)
    213 if ismath:
    214     ox, oy, width, height, descent, font_image = \
    215         self.mathtext_parser.parse(s, self.dpi, prop)

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/backend_bases.py:566, in RendererBase.get_text_width_height_descent(self, s, prop, ismath)
    562 fontsize = prop.get_size_in_points()
    564 if ismath == 'TeX':
    565     # todo: handle properties
--> 566     return self.get_texmanager().get_text_width_height_descent(
    567         s, fontsize, renderer=self)
    569 dpi = self.points_to_pixels(72)
    570 if ismath:

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/texmanager.py:364, in TexManager.get_text_width_height_descent(cls, tex, fontsize, renderer)
    362 if tex.strip() == '':
    363     return 0, 0, 0
--> 364 dvifile = cls.make_dvi(tex, fontsize)
    365 dpi_fraction = renderer.points_to_pixels(1.) if renderer else 1
    366 with dviread.Dvi(dvifile, 72 * dpi_fraction) as dvi:

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/texmanager.py:293, in TexManager.make_dvi(cls, tex, fontsize)
    290 with TemporaryDirectory(dir=dvifile.parent) as tmpdir:
    291     Path(tmpdir, "file.tex").write_text(
    292         cls._get_tex_source(tex, fontsize), encoding='utf-8')
--> 293     cls._run_checked_subprocess(
    294         ["latex", "-interaction=nonstopmode", "-halt-on-error",
    295          "-no-shell-escape", "file.tex"], tex, cwd=tmpdir)
    296     Path(tmpdir, "file.dvi").replace(dvifile)
    297     # Also move the tex source to the main cache directory, but
    298     # only for backcompat.

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/texmanager.py:254, in TexManager._run_checked_subprocess(cls, command, tex, cwd)
    250     report = subprocess.check_output(
    251         command, cwd=cwd if cwd is not None else cls._texcache,
    252         stderr=subprocess.STDOUT)
    253 except FileNotFoundError as exc:
--> 254     raise RuntimeError(
    255         f'Failed to process string with tex because {command[0]} '
    256         'could not be found') from exc
    257 except subprocess.CalledProcessError as exc:
    258     raise RuntimeError(
    259         '{prog} was not able to process the following string:\n'
    260         '{tex!r}\n\n'
   (...)    267             exc=exc.output.decode('utf-8', 'backslashreplace'))
    268         ) from None

RuntimeError: Failed to process string with tex because latex could not be found

<Figure size 640x480 with 1 Axes>

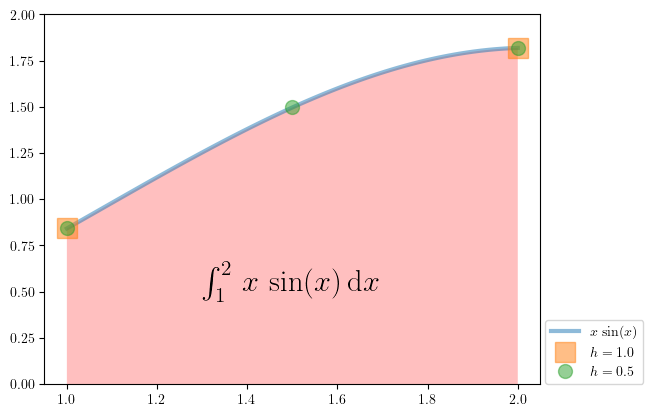
Analitično izračunajmo točen rezultat:

import sympy as sym
sym.init_printing()
x = sym.symbols('x')
I_točno = float(sym.integrate(x*sym.sin(x), (x, 1, 2)).evalf())
I_točno

\[\displaystyle 1.44042242098021\]

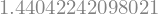
Newton-Cotesov pristop

Na sliki je prikazan splošen primer, kjer je razdalja med vozlišči \(x_i\) enaka \(h\) (gre za ekvidistantno delitev).

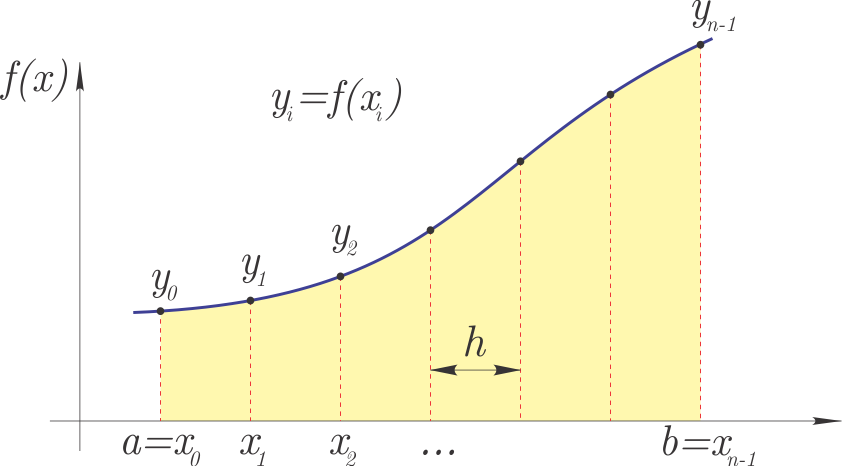
V okviru tega poglavja si bomo najprej pogledali trapezno ter sestavljeno trapezno pravilo, pozneje pa bosta sledili še Simpsonova ter Rombergova metoda.

Trapezno pravilo

Trapezno pravilo vrednosti podintegralske funkcije \(f(x)\) na (pod)intervalu \([x_0, x_1]\) interpolira z linearno funkcijo. Za dve vozliščni točki to pomeni, da površino pod grafom funkcije približno izračunamo kot:

\[I_{\textrm{trapezno}}=\sum_{i=0}^{n=1}A_i\,f(x_i)=\frac{h}{2}\cdot\left(f(x_0)+f(x_1)\right).\]

In so uteži:

\[A_0 = A_1 = \frac{1}{2}\,h.\]

Numerična implementacija

Numerična implementacija je:

def trapezno(y, h):
    """
    Trapezno pravilo integriranja.
    
    :param y: funkcijske vrednosti
    :param h: korak integriranja
    """
    return (y[0] + y[-1])*h/2

Numerični zgled

V konkretnem primeru to pomeni, da prvo in zadnjo funkcijsko vrednost utežimo s \(h/2\). V našem primeru je \(h=1\):

I_trapezno = trapezno(y2v, h=h2v)
I_trapezno

\[\displaystyle 1.33003291922963\]

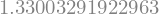
Pripravimo sliko:

def fig_trapezno():
    plt.fill_between(x2v, y2v, alpha=0.25, facecolor='r')
    plt.vlines(x2v, 0, y2v, color='r', linestyles='dashed', lw=1)
    plt.annotate('$I_{\\textrm{trapezno}}$', (1.4, 0.5), fontsize=22)
    plt.annotate('Napaka', fontsize=20, xy=(1.5, 1.4), xytext=(1.6, 1.8),
            arrowprops=dict(facecolor='gray', shrink=0.05))
    plt.plot(xg, yg, lw=3, alpha=0.5, label='$x\\,\\sin(x)$')
    plt.plot(x2v, y2v, 'o', alpha=0.5, label=f'$h={h2v}$')
    plt.legend(loc=(1.01, 0))
    plt.ylim(0, 2)
    plt.show()

Prikažemo:

fig_trapezno()

---------------------------------------------------------------------------
FileNotFoundError                         Traceback (most recent call last)
File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/texmanager.py:250, in TexManager._run_checked_subprocess(cls, command, tex, cwd)
    249 try:
--> 250     report = subprocess.check_output(
    251         command, cwd=cwd if cwd is not None else cls._texcache,
    252         stderr=subprocess.STDOUT)
    253 except FileNotFoundError as exc:

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/subprocess.py:466, in check_output(timeout, *popenargs, **kwargs)
    464     kwargs['input'] = empty
--> 466 return run(*popenargs, stdout=PIPE, timeout=timeout, check=True,
    467            **kwargs).stdout

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/subprocess.py:548, in run(input, capture_output, timeout, check, *popenargs, **kwargs)
    546     kwargs['stderr'] = PIPE
--> 548 with Popen(*popenargs, **kwargs) as process:
    549     try:

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/subprocess.py:1026, in Popen.__init__(self, args, bufsize, executable, stdin, stdout, stderr, preexec_fn, close_fds, shell, cwd, env, universal_newlines, startupinfo, creationflags, restore_signals, start_new_session, pass_fds, user, group, extra_groups, encoding, errors, text, umask, pipesize, process_group)
   1023             self.stderr = io.TextIOWrapper(self.stderr,
   1024                     encoding=encoding, errors=errors)
-> 1026     self._execute_child(args, executable, preexec_fn, close_fds,
   1027                         pass_fds, cwd, env,
   1028                         startupinfo, creationflags, shell,
   1029                         p2cread, p2cwrite,
   1030                         c2pread, c2pwrite,
   1031                         errread, errwrite,
   1032                         restore_signals,
   1033                         gid, gids, uid, umask,
   1034                         start_new_session, process_group)
   1035 except:
   1036     # Cleanup if the child failed starting.

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/subprocess.py:1955, in Popen._execute_child(self, args, executable, preexec_fn, close_fds, pass_fds, cwd, env, startupinfo, creationflags, shell, p2cread, p2cwrite, c2pread, c2pwrite, errread, errwrite, restore_signals, gid, gids, uid, umask, start_new_session, process_group)
   1954 if err_filename is not None:
-> 1955     raise child_exception_type(errno_num, err_msg, err_filename)
   1956 else:

FileNotFoundError: [Errno 2] No such file or directory: 'latex'

The above exception was the direct cause of the following exception:

RuntimeError                              Traceback (most recent call last)
File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/backend_bases.py:2157, in FigureCanvasBase.print_figure(self, filename, dpi, facecolor, edgecolor, orientation, format, bbox_inches, pad_inches, bbox_extra_artists, backend, **kwargs)
   2154     # we do this instead of `self.figure.draw_without_rendering`
   2155     # so that we can inject the orientation
   2156     with getattr(renderer, "_draw_disabled", nullcontext)():
-> 2157         self.figure.draw(renderer)
   2158 if bbox_inches:
   2159     if bbox_inches == "tight":

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/artist.py:94, in _finalize_rasterization.<locals>.draw_wrapper(artist, renderer, *args, **kwargs)
     92 @wraps(draw)
     93 def draw_wrapper(artist, renderer, *args, **kwargs):
---> 94     result = draw(artist, renderer, *args, **kwargs)
     95     if renderer._rasterizing:
     96         renderer.stop_rasterizing()

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/artist.py:71, in allow_rasterization.<locals>.draw_wrapper(artist, renderer)
     68     if artist.get_agg_filter() is not None:
     69         renderer.start_filter()
---> 71     return draw(artist, renderer)
     72 finally:
     73     if artist.get_agg_filter() is not None:

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/figure.py:3264, in Figure.draw(self, renderer)
   3261             # ValueError can occur when resizing a window.
   3263     self.patch.draw(renderer)
-> 3264     mimage._draw_list_compositing_images(
   3265         renderer, self, artists, self.suppressComposite)
   3267     renderer.close_group('figure')
   3268 finally:

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/image.py:134, in _draw_list_compositing_images(renderer, parent, artists, suppress_composite)
    132 if not_composite or not has_images:
    133     for a in artists:
--> 134         a.draw(renderer)
    135 else:
    136     # Composite any adjacent images together
    137     image_group = []

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/artist.py:71, in allow_rasterization.<locals>.draw_wrapper(artist, renderer)
     68     if artist.get_agg_filter() is not None:
     69         renderer.start_filter()
---> 71     return draw(artist, renderer)
     72 finally:
     73     if artist.get_agg_filter() is not None:

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/axes/_base.py:3226, in _AxesBase.draw(self, renderer)
   3223 if artists_rasterized:
   3224     _draw_rasterized(self.get_figure(root=True), artists_rasterized, renderer)
-> 3226 mimage._draw_list_compositing_images(
   3227     renderer, self, artists, self.get_figure(root=True).suppressComposite)
   3229 renderer.close_group('axes')
   3230 self.stale = False

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/image.py:134, in _draw_list_compositing_images(renderer, parent, artists, suppress_composite)
    132 if not_composite or not has_images:
    133     for a in artists:
--> 134         a.draw(renderer)
    135 else:
    136     # Composite any adjacent images together
    137     image_group = []

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/artist.py:71, in allow_rasterization.<locals>.draw_wrapper(artist, renderer)
     68     if artist.get_agg_filter() is not None:
     69         renderer.start_filter()
---> 71     return draw(artist, renderer)
     72 finally:
     73     if artist.get_agg_filter() is not None:

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/axis.py:1405, in Axis.draw(self, renderer)
   1402 renderer.open_group(__name__, gid=self.get_gid())
   1404 ticks_to_draw = self._update_ticks()
-> 1405 tlb1, tlb2 = self._get_ticklabel_bboxes(ticks_to_draw, renderer)
   1407 for tick in ticks_to_draw:
   1408     tick.draw(renderer)

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/axis.py:1332, in Axis._get_ticklabel_bboxes(self, ticks, renderer)
   1330 if renderer is None:
   1331     renderer = self.get_figure(root=True)._get_renderer()
-> 1332 return ([tick.label1.get_window_extent(renderer)
   1333          for tick in ticks if tick.label1.get_visible()],
   1334         [tick.label2.get_window_extent(renderer)
   1335          for tick in ticks if tick.label2.get_visible()])

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/axis.py:1332, in <listcomp>(.0)
   1330 if renderer is None:
   1331     renderer = self.get_figure(root=True)._get_renderer()
-> 1332 return ([tick.label1.get_window_extent(renderer)
   1333          for tick in ticks if tick.label1.get_visible()],
   1334         [tick.label2.get_window_extent(renderer)
   1335          for tick in ticks if tick.label2.get_visible()])

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/text.py:969, in Text.get_window_extent(self, renderer, dpi)
    964     raise RuntimeError(
    965         "Cannot get window extent of text w/o renderer. You likely "
    966         "want to call 'figure.draw_without_rendering()' first.")
    968 with cbook._setattr_cm(fig, dpi=dpi):
--> 969     bbox, info, descent = self._get_layout(self._renderer)
    970     x, y = self.get_unitless_position()
    971     x, y = self.get_transform().transform((x, y))

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/text.py:373, in Text._get_layout(self, renderer)
    370 ys = []
    372 # Full vertical extent of font, including ascenders and descenders:
--> 373 _, lp_h, lp_d = _get_text_metrics_with_cache(
    374     renderer, "lp", self._fontproperties,
    375     ismath="TeX" if self.get_usetex() else False,
    376     dpi=self.get_figure(root=True).dpi)
    377 min_dy = (lp_h - lp_d) * self._linespacing
    379 for i, line in enumerate(lines):

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/text.py:69, in _get_text_metrics_with_cache(renderer, text, fontprop, ismath, dpi)
     66 """Call ``renderer.get_text_width_height_descent``, caching the results."""
     67 # Cached based on a copy of fontprop so that later in-place mutations of
     68 # the passed-in argument do not mess up the cache.
---> 69 return _get_text_metrics_with_cache_impl(
     70     weakref.ref(renderer), text, fontprop.copy(), ismath, dpi)

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/text.py:77, in _get_text_metrics_with_cache_impl(renderer_ref, text, fontprop, ismath, dpi)
     73 @functools.lru_cache(4096)
     74 def _get_text_metrics_with_cache_impl(
     75         renderer_ref, text, fontprop, ismath, dpi):
     76     # dpi is unused, but participates in cache invalidation (via the renderer).
---> 77     return renderer_ref().get_text_width_height_descent(text, fontprop, ismath)

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/backends/backend_agg.py:211, in RendererAgg.get_text_width_height_descent(self, s, prop, ismath)
    209 _api.check_in_list(["TeX", True, False], ismath=ismath)
    210 if ismath == "TeX":
--> 211     return super().get_text_width_height_descent(s, prop, ismath)
    213 if ismath:
    214     ox, oy, width, height, descent, font_image = \
    215         self.mathtext_parser.parse(s, self.dpi, prop)

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/backend_bases.py:566, in RendererBase.get_text_width_height_descent(self, s, prop, ismath)
    562 fontsize = prop.get_size_in_points()
    564 if ismath == 'TeX':
    565     # todo: handle properties
--> 566     return self.get_texmanager().get_text_width_height_descent(
    567         s, fontsize, renderer=self)
    569 dpi = self.points_to_pixels(72)
    570 if ismath:

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/texmanager.py:364, in TexManager.get_text_width_height_descent(cls, tex, fontsize, renderer)
    362 if tex.strip() == '':
    363     return 0, 0, 0
--> 364 dvifile = cls.make_dvi(tex, fontsize)
    365 dpi_fraction = renderer.points_to_pixels(1.) if renderer else 1
    366 with dviread.Dvi(dvifile, 72 * dpi_fraction) as dvi:

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/texmanager.py:293, in TexManager.make_dvi(cls, tex, fontsize)
    290 with TemporaryDirectory(dir=dvifile.parent) as tmpdir:
    291     Path(tmpdir, "file.tex").write_text(
    292         cls._get_tex_source(tex, fontsize), encoding='utf-8')
--> 293     cls._run_checked_subprocess(
    294         ["latex", "-interaction=nonstopmode", "-halt-on-error",
    295          "-no-shell-escape", "file.tex"], tex, cwd=tmpdir)
    296     Path(tmpdir, "file.dvi").replace(dvifile)
    297     # Also move the tex source to the main cache directory, but
    298     # only for backcompat.

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/texmanager.py:254, in TexManager._run_checked_subprocess(cls, command, tex, cwd)
    250     report = subprocess.check_output(
    251         command, cwd=cwd if cwd is not None else cls._texcache,
    252         stderr=subprocess.STDOUT)
    253 except FileNotFoundError as exc:
--> 254     raise RuntimeError(
    255         f'Failed to process string with tex because {command[0]} '
    256         'could not be found') from exc
    257 except subprocess.CalledProcessError as exc:
    258     raise RuntimeError(
    259         '{prog} was not able to process the following string:\n'
    260         '{tex!r}\n\n'
   (...)    267             exc=exc.output.decode('utf-8', 'backslashreplace'))
    268         ) from None

RuntimeError: Failed to process string with tex because latex could not be found

<Figure size 640x480 with 1 Axes>

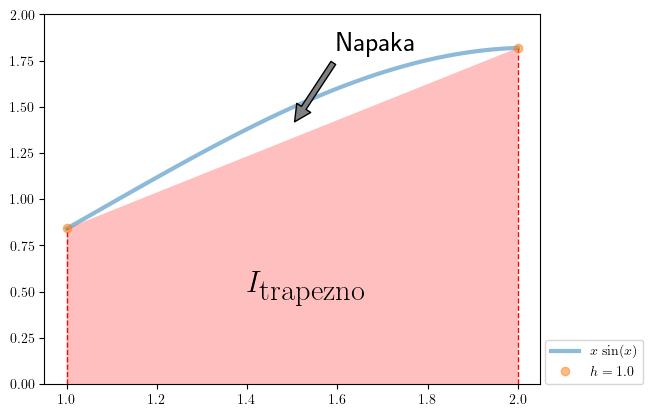
Napaka trapeznega pravila

Razlika med analitično vrednostjo integrala in numeričnim približkom \(I\) je napaka metode:

\[E = \int_a^bf(x)\,d x-I,\]

Če je funkcija \(f(x)\) vsaj dvakrat odvedljiva, se lahko (glejte npr. vir: Burden, Faires, Burden: Numerical Analysis 10th Ed) izpelje ocena napake, ki velja samo za trapezni približek prek celega integracijskega intervala:

\[E_{\textrm{trapezno}}=-\frac{h^3}{12}f''(\xi),\]

kjer je \(h=b-a\) in \(\xi\) neznana vrednost na intervalu \([a,b]\).

Sestavljeno trapezno pravilo

Če razdelimo interval \([a, b]\) na \(n\) podintervalov in na vsakem uporabimo trapezno pravilo integriranja, govorimo o sestavljenem trapeznem pravilu (angl. composite trapezoidal rule).

V tem primeru za vsak podinterval \(i\) uporabimo trapezno pravilo in torej za meje podinterval \(x_i\) in \(x_{i+1}\) uporabimo uteži \(A_i=A_{i+i}=h/2\). Ker so notranja vozlišča podvojena, sledi:

\[A_0=A_{n}=\frac{h}{2}\quad\textrm{in za ostala vozlišča:}\quad A_i=h.\]

Pri tem smo predpostavili podintervale enake širine:

\[h=\frac{x_{n}-x_0}{n}\]

Sledi torej:

\[I_{\textrm{trapezno sest}}=\sum_{i=0}^{n}A_i\,f(x_i)=\left(\frac{y_0}{2} + y_1+y_2+\cdots+y_{n-1}+\frac{y_{n}}{2}\right)\,h.\]

Numerična implementacija

Numerična implementacija je:

def trapezno_sest(y, h):
    """
    Sestavljeno trapezno pravilo integriranja.
    
    :param y: funkcijske vrednosti
    :param h: korak integriranja
    """    
    return (np.sum(y) - 0.5*y[0] - 0.5*y[-1])*h

Numerični zgled

Zgoraj smo že pripravili podatke za dva podintervala (tri vozlišča):

x3v

array([1. , 1.5, 2. ])

h3v

\[\displaystyle 0.5\]

Izračunajmo oceno integrala s sestavljenim trapeznim pravilom:

I_trapezno_sest = trapezno_sest(y3v, h=h3v)
I_trapezno_sest

\[\displaystyle 1.41313769956786\]

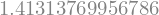
Pripravimo sliko:

def fig_trapezno_sest():
    plt.fill_between(x3v, y3v, alpha=0.25, facecolor='r')
    plt.vlines(x3v, 0, y3v, color='r', linestyles='dashed', lw=1)
    plt.annotate('$I_{\\textrm{trapezno sestavljeno}}$', (1.2, 0.5), fontsize=22)
    plt.annotate('Napaka', fontsize=20, xy=(1.75, 1.68), xytext=(1.4, 1.8),
            arrowprops=dict(facecolor='gray', shrink=0.05))
    plt.annotate('Napaka', fontsize=20, xy=(1.2, 1.1), xytext=(1., 1.4),
            arrowprops=dict(facecolor='gray', shrink=0.05))
    plt.plot(xg, yg, lw=3, alpha=0.5, label='$x\\,\\sin(x)$')
    plt.plot(x3v, y3v, 'o', alpha=0.5, label=f'$h={h3v}$')
    plt.legend(loc=(1.01, 0))
    plt.ylim(0, 2)
    plt.show()

Prikažemo:

fig_trapezno_sest()

---------------------------------------------------------------------------
FileNotFoundError                         Traceback (most recent call last)
File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/texmanager.py:250, in TexManager._run_checked_subprocess(cls, command, tex, cwd)
    249 try:
--> 250     report = subprocess.check_output(
    251         command, cwd=cwd if cwd is not None else cls._texcache,
    252         stderr=subprocess.STDOUT)
    253 except FileNotFoundError as exc:

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/subprocess.py:466, in check_output(timeout, *popenargs, **kwargs)
    464     kwargs['input'] = empty
--> 466 return run(*popenargs, stdout=PIPE, timeout=timeout, check=True,
    467            **kwargs).stdout

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/subprocess.py:548, in run(input, capture_output, timeout, check, *popenargs, **kwargs)
    546     kwargs['stderr'] = PIPE
--> 548 with Popen(*popenargs, **kwargs) as process:
    549     try:

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/subprocess.py:1026, in Popen.__init__(self, args, bufsize, executable, stdin, stdout, stderr, preexec_fn, close_fds, shell, cwd, env, universal_newlines, startupinfo, creationflags, restore_signals, start_new_session, pass_fds, user, group, extra_groups, encoding, errors, text, umask, pipesize, process_group)
   1023             self.stderr = io.TextIOWrapper(self.stderr,
   1024                     encoding=encoding, errors=errors)
-> 1026     self._execute_child(args, executable, preexec_fn, close_fds,
   1027                         pass_fds, cwd, env,
   1028                         startupinfo, creationflags, shell,
   1029                         p2cread, p2cwrite,
   1030                         c2pread, c2pwrite,
   1031                         errread, errwrite,
   1032                         restore_signals,
   1033                         gid, gids, uid, umask,
   1034                         start_new_session, process_group)
   1035 except:
   1036     # Cleanup if the child failed starting.

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/subprocess.py:1955, in Popen._execute_child(self, args, executable, preexec_fn, close_fds, pass_fds, cwd, env, startupinfo, creationflags, shell, p2cread, p2cwrite, c2pread, c2pwrite, errread, errwrite, restore_signals, gid, gids, uid, umask, start_new_session, process_group)
   1954 if err_filename is not None:
-> 1955     raise child_exception_type(errno_num, err_msg, err_filename)
   1956 else:

FileNotFoundError: [Errno 2] No such file or directory: 'latex'

The above exception was the direct cause of the following exception:

RuntimeError                              Traceback (most recent call last)
File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/backend_bases.py:2157, in FigureCanvasBase.print_figure(self, filename, dpi, facecolor, edgecolor, orientation, format, bbox_inches, pad_inches, bbox_extra_artists, backend, **kwargs)
   2154     # we do this instead of `self.figure.draw_without_rendering`
   2155     # so that we can inject the orientation
   2156     with getattr(renderer, "_draw_disabled", nullcontext)():
-> 2157         self.figure.draw(renderer)
   2158 if bbox_inches:
   2159     if bbox_inches == "tight":

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/artist.py:94, in _finalize_rasterization.<locals>.draw_wrapper(artist, renderer, *args, **kwargs)
     92 @wraps(draw)
     93 def draw_wrapper(artist, renderer, *args, **kwargs):
---> 94     result = draw(artist, renderer, *args, **kwargs)
     95     if renderer._rasterizing:
     96         renderer.stop_rasterizing()

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/artist.py:71, in allow_rasterization.<locals>.draw_wrapper(artist, renderer)
     68     if artist.get_agg_filter() is not None:
     69         renderer.start_filter()
---> 71     return draw(artist, renderer)
     72 finally:
     73     if artist.get_agg_filter() is not None:

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/figure.py:3264, in Figure.draw(self, renderer)
   3261             # ValueError can occur when resizing a window.
   3263     self.patch.draw(renderer)
-> 3264     mimage._draw_list_compositing_images(
   3265         renderer, self, artists, self.suppressComposite)
   3267     renderer.close_group('figure')
   3268 finally:

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/image.py:134, in _draw_list_compositing_images(renderer, parent, artists, suppress_composite)
    132 if not_composite or not has_images:
    133     for a in artists:
--> 134         a.draw(renderer)
    135 else:
    136     # Composite any adjacent images together
    137     image_group = []

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/artist.py:71, in allow_rasterization.<locals>.draw_wrapper(artist, renderer)
     68     if artist.get_agg_filter() is not None:
     69         renderer.start_filter()
---> 71     return draw(artist, renderer)
     72 finally:
     73     if artist.get_agg_filter() is not None:

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/axes/_base.py:3226, in _AxesBase.draw(self, renderer)
   3223 if artists_rasterized:
   3224     _draw_rasterized(self.get_figure(root=True), artists_rasterized, renderer)
-> 3226 mimage._draw_list_compositing_images(
   3227     renderer, self, artists, self.get_figure(root=True).suppressComposite)
   3229 renderer.close_group('axes')
   3230 self.stale = False

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/image.py:134, in _draw_list_compositing_images(renderer, parent, artists, suppress_composite)
    132 if not_composite or not has_images:
    133     for a in artists:
--> 134         a.draw(renderer)
    135 else:
    136     # Composite any adjacent images together
    137     image_group = []

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/artist.py:71, in allow_rasterization.<locals>.draw_wrapper(artist, renderer)
     68     if artist.get_agg_filter() is not None:
     69         renderer.start_filter()
---> 71     return draw(artist, renderer)
     72 finally:
     73     if artist.get_agg_filter() is not None:

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/axis.py:1405, in Axis.draw(self, renderer)
   1402 renderer.open_group(__name__, gid=self.get_gid())
   1404 ticks_to_draw = self._update_ticks()
-> 1405 tlb1, tlb2 = self._get_ticklabel_bboxes(ticks_to_draw, renderer)
   1407 for tick in ticks_to_draw:
   1408     tick.draw(renderer)

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/axis.py:1332, in Axis._get_ticklabel_bboxes(self, ticks, renderer)
   1330 if renderer is None:
   1331     renderer = self.get_figure(root=True)._get_renderer()
-> 1332 return ([tick.label1.get_window_extent(renderer)
   1333          for tick in ticks if tick.label1.get_visible()],
   1334         [tick.label2.get_window_extent(renderer)
   1335          for tick in ticks if tick.label2.get_visible()])

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/axis.py:1332, in <listcomp>(.0)
   1330 if renderer is None:
   1331     renderer = self.get_figure(root=True)._get_renderer()
-> 1332 return ([tick.label1.get_window_extent(renderer)
   1333          for tick in ticks if tick.label1.get_visible()],
   1334         [tick.label2.get_window_extent(renderer)
   1335          for tick in ticks if tick.label2.get_visible()])

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/text.py:969, in Text.get_window_extent(self, renderer, dpi)
    964     raise RuntimeError(
    965         "Cannot get window extent of text w/o renderer. You likely "
    966         "want to call 'figure.draw_without_rendering()' first.")
    968 with cbook._setattr_cm(fig, dpi=dpi):
--> 969     bbox, info, descent = self._get_layout(self._renderer)
    970     x, y = self.get_unitless_position()
    971     x, y = self.get_transform().transform((x, y))

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/text.py:373, in Text._get_layout(self, renderer)
    370 ys = []
    372 # Full vertical extent of font, including ascenders and descenders:
--> 373 _, lp_h, lp_d = _get_text_metrics_with_cache(
    374     renderer, "lp", self._fontproperties,
    375     ismath="TeX" if self.get_usetex() else False,
    376     dpi=self.get_figure(root=True).dpi)
    377 min_dy = (lp_h - lp_d) * self._linespacing
    379 for i, line in enumerate(lines):

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/text.py:69, in _get_text_metrics_with_cache(renderer, text, fontprop, ismath, dpi)
     66 """Call ``renderer.get_text_width_height_descent``, caching the results."""
     67 # Cached based on a copy of fontprop so that later in-place mutations of
     68 # the passed-in argument do not mess up the cache.
---> 69 return _get_text_metrics_with_cache_impl(
     70     weakref.ref(renderer), text, fontprop.copy(), ismath, dpi)

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/text.py:77, in _get_text_metrics_with_cache_impl(renderer_ref, text, fontprop, ismath, dpi)
     73 @functools.lru_cache(4096)
     74 def _get_text_metrics_with_cache_impl(
     75         renderer_ref, text, fontprop, ismath, dpi):
     76     # dpi is unused, but participates in cache invalidation (via the renderer).
---> 77     return renderer_ref().get_text_width_height_descent(text, fontprop, ismath)

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/backends/backend_agg.py:211, in RendererAgg.get_text_width_height_descent(self, s, prop, ismath)
    209 _api.check_in_list(["TeX", True, False], ismath=ismath)
    210 if ismath == "TeX":
--> 211     return super().get_text_width_height_descent(s, prop, ismath)
    213 if ismath:
    214     ox, oy, width, height, descent, font_image = \
    215         self.mathtext_parser.parse(s, self.dpi, prop)

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/backend_bases.py:566, in RendererBase.get_text_width_height_descent(self, s, prop, ismath)
    562 fontsize = prop.get_size_in_points()
    564 if ismath == 'TeX':
    565     # todo: handle properties
--> 566     return self.get_texmanager().get_text_width_height_descent(
    567         s, fontsize, renderer=self)
    569 dpi = self.points_to_pixels(72)
    570 if ismath:

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/texmanager.py:364, in TexManager.get_text_width_height_descent(cls, tex, fontsize, renderer)
    362 if tex.strip() == '':
    363     return 0, 0, 0
--> 364 dvifile = cls.make_dvi(tex, fontsize)
    365 dpi_fraction = renderer.points_to_pixels(1.) if renderer else 1
    366 with dviread.Dvi(dvifile, 72 * dpi_fraction) as dvi:

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/texmanager.py:293, in TexManager.make_dvi(cls, tex, fontsize)
    290 with TemporaryDirectory(dir=dvifile.parent) as tmpdir:
    291     Path(tmpdir, "file.tex").write_text(
    292         cls._get_tex_source(tex, fontsize), encoding='utf-8')
--> 293     cls._run_checked_subprocess(
    294         ["latex", "-interaction=nonstopmode", "-halt-on-error",
    295          "-no-shell-escape", "file.tex"], tex, cwd=tmpdir)
    296     Path(tmpdir, "file.dvi").replace(dvifile)
    297     # Also move the tex source to the main cache directory, but
    298     # only for backcompat.

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/texmanager.py:254, in TexManager._run_checked_subprocess(cls, command, tex, cwd)
    250     report = subprocess.check_output(
    251         command, cwd=cwd if cwd is not None else cls._texcache,
    252         stderr=subprocess.STDOUT)
    253 except FileNotFoundError as exc:
--> 254     raise RuntimeError(
    255         f'Failed to process string with tex because {command[0]} '
    256         'could not be found') from exc
    257 except subprocess.CalledProcessError as exc:
    258     raise RuntimeError(
    259         '{prog} was not able to process the following string:\n'
    260         '{tex!r}\n\n'
   (...)    267             exc=exc.output.decode('utf-8', 'backslashreplace'))
    268         ) from None

RuntimeError: Failed to process string with tex because latex could not be found

<Figure size 640x480 with 1 Axes>

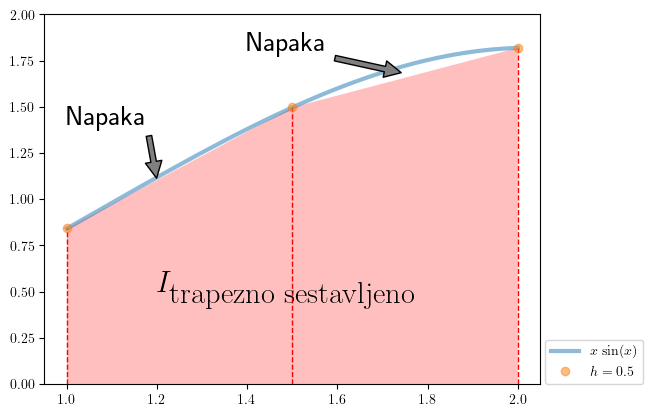
Napaka sestavljenega trapeznega pravila

Napaka sestavljenega trapeznega pravila izhaja iz napake trapeznega pravila; pri tem tako napako naredimo \(n\)-krat.

Ker velja \(h\cdot n=b-a\), izpeljemo napako sestavljenega trapeznega pravila kot:

\[E_{\textrm{trapezno sest}}=-\frac{h^2(b-a)}{12}f''(\eta),\]

\(\eta\) je vrednost na intervalu \([a,b]\). Napaka je drugega reda \(\mathcal{O}(h^2)\).

Boljši približek integrala

V nadaljevanju si bomo pogledali t. i. Richardsonovo ekstrapolacijo, pri kateri na podlagi ocene integrala s korakom \(h\) in \(2h\) izračunamo boljši približek.

V kolikor integral \(I\) numerično izračunamo pri dveh različnih korakih \(h\) in \(2\,h\), velja:

\[\int_a^b f(x)\,\textrm{d}x = I_h + E_h = I_{2h} + E_{2h},\]

kjer sta \(I_h\) in \(I_{2h}\) približka integrala s korakom \(h\) in \(2h\) ter \(E_h\) in \(E_{2h}\) oceni napake pri koraku \(h\) in \(2h\). Izpeljemo \(I_{2h}-I_{h} = E_{h}-E_{2h}\)

Naprej zapišemo:

\[E_h=-\frac{h^2(b-a)}{12}f''(\eta)=h^2\,K.\]

Ob predpostavki, da je \(f''\left (\eta \right )\) pri koraku \(h\) in \(2h\) enak (\(\eta\) je pri koraku \(h\) in \(2h\) dejansko različen), zapišemo:

\[E_{2h}=-\frac{(2h)^2(b-a)}{12}f''(\eta)=4\,h^2\,K\]

Sledi:

\[I_{2h}-I_h=-3K\,h^2.\]

Sedaj lahko ocenimo napako pri koraku \(h\):

\[E_h=h^2\,K=\frac{I_h-I_{2h}}{3}.\]

Na podlagi ocene napake lahko izračunamo boljši numerični približek \(I_{h}^*\):

\[I_h^* = I_h + \frac{1}{3}\,(I_{h}-I_{2h})\]

ali

\[I_h^* = \frac{4}{3}\,I_h - \frac{1}{3}\,I_{2h}\]

Numerični zgled

Predhodno smo s trapeznim pravilom že izračunali integral pri koraku \(h=1\) in pri koraku \(h=0,5\), rezultata sta bila:

[I_trapezno, I_trapezno_sest]

\[\displaystyle \left[ 1.33003291922963, \ 1.41313769956786\right]\]

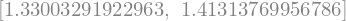
S pomočjo zgornje formule izračunamo boljši približek:

I_trapezno_boljši = 4/3*I_trapezno_sest - 1/3*I_trapezno
print(f'Točen rezultat:   {I_točno}\nBoljši približek: {I_trapezno_boljši}')

Točen rezultat:   1.4404224209802097
Boljši približek: 1.4408392930139313

Sestavljeno trapezno pravilo je implementirano tudi v paketu numpy, s funkcijo numpy.trapz:

trapz(y, x=None, dx=1.0, axis=-1)

• y predstavlja tabelo funkcijskih vrednosti,

• x je opcijski parameter in definira vozlišča; če parameter ni definiran, se privzame ekvidistančna vozlišča na razdalji dx,

• dx definira (konstanten) korak integracije, ima privzeto vrednost 1,

• axis definira os po kateri se integrira (v primeru, da je y večdimenzijsko numerično polje).

Funkcija vrne izračunani integral po sestavljenem trapeznem pravilu. Več informacij lahko najdete v dokumentaciji.

numpy implementacija sestavljenega trapeznega pravila

Poglejmo si primer:

#%%timeit
I_trapezno_np = np.trapezoid(y3v, dx=h3v)
I_trapezno_np

\[\displaystyle 1.41313769956786\]

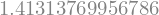
Simpsonova in druge metode

Zgoraj smo si pogledali trapezno pravilo, ki temelji na linearni interpolacijski funkciji na posameznem podintervalu. Z interpolacijo višjega reda lahko izpeljemo še druge integracijske metode.

Izračunati moramo:

\[\int_{a}^b f(x)\,dx.\]

Tabeliramo podintegralsko funkcijo \(f(x)\) in tabelo interpoliramo z Lagrangevim interpolacijskim polinomom \(P_n(x)\) stopnje \(n\):

\[P_n(x)=\sum_{i=0}^{n}\,f(x_i)\,l_i(x),\]

kjer so \(y_i=f(x_i)\) funkcijske vrednosti v vozliščih \(x_i\) in je Lagrangev polinom \(l_i\) definiran kot:

\[l_i(x)=\prod_{j=0, j\ne i}^n \frac{x-x_j}{x_i-x_j}.\]

Za numerični izračun integrala \(\int_{a}^b f(x)\,dx\) (meje so: \(a=x_0\), \(b=x_n\)) namesto funkcije \(f(x)\) vstavimo v integral interpolacijski polinom \(P_n(x)\):

\[I=\int_{x_0}^{x_{n}} P_n(x)\,dx=\int_{x_0}^{x_{n}} \sum_{i=0}^{n}\,f(x_i)\,l_i(x)\,dx.\]

Ker je integriranje linearna operacija, lahko zamenjamo integriranje in vsoto:

\[I=\sum_{i=0}^{n}\,f(x_i)\,\underbrace{\int_{x_0}^{x_{n}} l_i(x)\,dx}_{A_i}.\]

Lagrangev polinom integriramo in dobimo uteži \(A_i\):

\[A_i = \int_{x_0}^{x_{n}} l_i(x)\,dx\]

Izpeljava trapeznega pravila z uporabo Lagrangevih polinomov

Poglejmo si kako z Lagrangevim interpolacijskim polinomom prve stopnje strojno izpeljemo uteži \(A_i\) v primeru trapeznega pravila.

Najprej v simbolni obliki definirajmo spremenljivko x, vozlišči x0 in x1 ter korak h:

x, x0, x1, h = sym.symbols('x x0, x1, h')

Pripravimo Python funkcijo, ki v simbolni obliki vrne seznam \(n\) koeficientov Lagrangevih polinomov \([l_0(x), l_1(x),\dots, l_{n-1}(x)]\) stopnje \(n-1\):

def lagrange(n, x, vozlišča_predpona='x'):
    if isinstance(vozlišča_predpona, str):
        vozlišča = sym.symbols(f'{vozlišča_predpona}:{n}') 
    coeffs = []
    for i in range(0, n):
        numer = []
        denom = []

        for j in range(0, n):
            if i == j:
                continue

            numer.append(x    - vozlišča[j])
            denom.append(vozlišča[i] - vozlišča[j])
        
        numer = sym.Mul(*numer)
        denom = sym.Mul(*denom)

        coeffs.append(numer/denom)
    return coeffs    

Najprej poglejmo Lagrangeva polinoma za linearno interpolacijo (\(n=2\)):

lag = lagrange(2, x)
lag

\[\displaystyle \left[ \frac{x - x_{1}}{x_{0} - x_{1}}, \ \frac{x - x_{0}}{- x_{0} + x_{1}}\right]\]

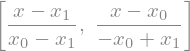
Sedaj Lagrangev polinom \(l_0(x)\) integriramo čez celotni interval:

int0 = sym.integrate(lag[0], (x, x0, x1))
int0

\[\displaystyle - \frac{x_{0}^{2}}{2 x_{0} - 2 x_{1}} + \frac{x_{0} x_{1}}{x_{0} - x_{1}} + \frac{x_{1}^{2}}{2 x_{0} - 2 x_{1}} - \frac{x_{1}^{2}}{x_{0} - x_{1}}\]

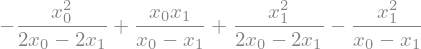
Izraz poenostavimo in dobimo:

int1 = int0.factor()
int1

\[\displaystyle - \frac{x_{0} - x_{1}}{2}\]

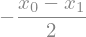
Ker je širina podintervala konstantna je \(x_1=h_0+h\), izvedemo zamenjavo:

zamenjave = {x1: x0+h}
int1.subs(zamenjave)

\[\displaystyle \frac{h}{2}\]

Zgornje korake za Lagrangev polinom \(l_0(x)\) lahko posplošimo za seznam Lagrangevih polinomov:

x, x0, x1, h = sym.symbols('x, x0, x1, h')
zamenjave = {x1: x0+h}
A_trapez = [sym.integrate(li, (x, x0, x1)).factor().subs(zamenjave) 
            for li in lagrange(2, x)]  # za vsak lagrangev polimom `li` v seznamu lagrange(2,x)
A_trapez

\[\displaystyle \left[ \frac{h}{2}, \ \frac{h}{2}\right]\]

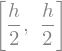
Izpeljali smo uteži, ki smo jih uporabili pri trapezni metodi:

\[A_0=h/2\qquad A_1=h/2.\]

Trapezno pravilo je:

\[I_{\textrm{trapezno}}=\frac{h}{2}\left(y_0+y_1\right)\]

Ocena napake je (vir: Burden, Faires, Burden: Numerical Analysis 10th Ed):

\[E_{\textrm{trapezno}}= -\frac{h^3}{12}f''(\xi).\]

Izračun uteži za Simpsonovo pravilo

Potem ko smo zgoraj pokazali strnjen izračun za trapezno pravilo, lahko podobno izvedemo za kvadratno interpolacijo čez tri točke (\(n=3\)).

Izračun uteži je analogen zgornjemu:

x, x0, x1, x2, h = sym.symbols('x, x0, x1, x2, h')
zamenjave = {x1: x0+h, x2: x0+2*h}
A_Simpson1_3 = [sym.integrate(li, (x, x0, x2)).factor().subs(zamenjave).factor() 
             for li in lagrange(3, x)]
A_Simpson1_3

\[\displaystyle \left[ \frac{h}{3}, \ \frac{4 h}{3}, \ \frac{h}{3}\right]\]

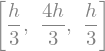
Simpsonovo pravilo (to pravilo se imenuje tudi Simpsonovo 1/3 pravilo) je:

\[I_{\textrm{Simpsonovo}}=\frac{h}{3}\left(y_0+4\,y_1+y_2\right)\]

Ocena napake je (vir: Burden, Faires, Burden: Numerical Analysis 10th Ed):

\[E_{\textrm{Simpsonovo}}= -\frac{h^5}{90}f^{(4)}(\xi).\]

Pri tem je treba izpostaviti, da je napaka lokalno 5 reda \(\mathcal{O}(h^5)\) in definirana z neznano vrednostjo četrtega odvoda \(f^{(4)}(\xi)\), posledično je to pravilo točno za polinome stopnje 3 ali manj.

Primer uporabe:

I_Simps = h3v/3 * np.sum(y3v * [1, 4, 1])
I_Simps

\[\displaystyle 1.44083929301393\]

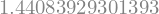
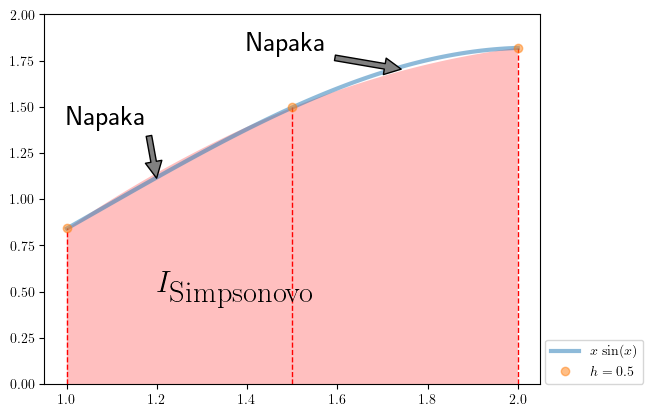
Pripravimo sliko. Ker Simsonovo pravilo temelji na kvadratni interpolaciji, moramo naprej pripraviti interpolacijski polinom (pomagamo si s scipy.interpolate):

from scipy import interpolate

def fig_Simpsonovo():
    y_interpolate = interpolate.lagrange(x3v, y3v)
    plt.fill_between(xg, y_interpolate(xg), alpha=0.25, facecolor='r')
    plt.vlines(x3v, 0, y3v, color='r', linestyles='dashed', lw=1)
    plt.annotate('$I_{\\textrm{Simpsonovo}}$', (1.2, 0.5), fontsize=22)
    plt.annotate('Napaka', fontsize=20, xy=(1.75, 1.7), xytext=(1.4, 1.8),
            arrowprops=dict(facecolor='gray', shrink=0.05))
    plt.annotate('Napaka', fontsize=20, xy=(1.2, 1.1), xytext=(1., 1.4),
            arrowprops=dict(facecolor='gray', shrink=0.05))
    plt.plot(xg, yg, lw=3, alpha=0.5, label='$x\\,\\sin(x)$')
    plt.plot(x3v, y3v, 'o', alpha=0.5, label=f'$h={h3v}$')
    plt.legend(loc=(1.01, 0))
    plt.ylim(0, 2)
    plt.show()

Prikažemo:

fig_Simpsonovo()

---------------------------------------------------------------------------
FileNotFoundError                         Traceback (most recent call last)
File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/texmanager.py:250, in TexManager._run_checked_subprocess(cls, command, tex, cwd)
    249 try:
--> 250     report = subprocess.check_output(
    251         command, cwd=cwd if cwd is not None else cls._texcache,
    252         stderr=subprocess.STDOUT)
    253 except FileNotFoundError as exc:

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/subprocess.py:466, in check_output(timeout, *popenargs, **kwargs)
    464     kwargs['input'] = empty
--> 466 return run(*popenargs, stdout=PIPE, timeout=timeout, check=True,
    467            **kwargs).stdout

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/subprocess.py:548, in run(input, capture_output, timeout, check, *popenargs, **kwargs)
    546     kwargs['stderr'] = PIPE
--> 548 with Popen(*popenargs, **kwargs) as process:
    549     try:

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/subprocess.py:1026, in Popen.__init__(self, args, bufsize, executable, stdin, stdout, stderr, preexec_fn, close_fds, shell, cwd, env, universal_newlines, startupinfo, creationflags, restore_signals, start_new_session, pass_fds, user, group, extra_groups, encoding, errors, text, umask, pipesize, process_group)
   1023             self.stderr = io.TextIOWrapper(self.stderr,
   1024                     encoding=encoding, errors=errors)
-> 1026     self._execute_child(args, executable, preexec_fn, close_fds,
   1027                         pass_fds, cwd, env,
   1028                         startupinfo, creationflags, shell,
   1029                         p2cread, p2cwrite,
   1030                         c2pread, c2pwrite,
   1031                         errread, errwrite,
   1032                         restore_signals,
   1033                         gid, gids, uid, umask,
   1034                         start_new_session, process_group)
   1035 except:
   1036     # Cleanup if the child failed starting.

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/subprocess.py:1955, in Popen._execute_child(self, args, executable, preexec_fn, close_fds, pass_fds, cwd, env, startupinfo, creationflags, shell, p2cread, p2cwrite, c2pread, c2pwrite, errread, errwrite, restore_signals, gid, gids, uid, umask, start_new_session, process_group)
   1954 if err_filename is not None:
-> 1955     raise child_exception_type(errno_num, err_msg, err_filename)
   1956 else:

FileNotFoundError: [Errno 2] No such file or directory: 'latex'

The above exception was the direct cause of the following exception:

RuntimeError                              Traceback (most recent call last)
File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/backend_bases.py:2157, in FigureCanvasBase.print_figure(self, filename, dpi, facecolor, edgecolor, orientation, format, bbox_inches, pad_inches, bbox_extra_artists, backend, **kwargs)
   2154     # we do this instead of `self.figure.draw_without_rendering`
   2155     # so that we can inject the orientation
   2156     with getattr(renderer, "_draw_disabled", nullcontext)():
-> 2157         self.figure.draw(renderer)
   2158 if bbox_inches:
   2159     if bbox_inches == "tight":

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/artist.py:94, in _finalize_rasterization.<locals>.draw_wrapper(artist, renderer, *args, **kwargs)
     92 @wraps(draw)
     93 def draw_wrapper(artist, renderer, *args, **kwargs):
---> 94     result = draw(artist, renderer, *args, **kwargs)
     95     if renderer._rasterizing:
     96         renderer.stop_rasterizing()

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/artist.py:71, in allow_rasterization.<locals>.draw_wrapper(artist, renderer)
     68     if artist.get_agg_filter() is not None:
     69         renderer.start_filter()
---> 71     return draw(artist, renderer)
     72 finally:
     73     if artist.get_agg_filter() is not None:

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/figure.py:3264, in Figure.draw(self, renderer)
   3261             # ValueError can occur when resizing a window.
   3263     self.patch.draw(renderer)
-> 3264     mimage._draw_list_compositing_images(
   3265         renderer, self, artists, self.suppressComposite)
   3267     renderer.close_group('figure')
   3268 finally:

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/image.py:134, in _draw_list_compositing_images(renderer, parent, artists, suppress_composite)
    132 if not_composite or not has_images:
    133     for a in artists:
--> 134         a.draw(renderer)
    135 else:
    136     # Composite any adjacent images together
    137     image_group = []

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/artist.py:71, in allow_rasterization.<locals>.draw_wrapper(artist, renderer)
     68     if artist.get_agg_filter() is not None:
     69         renderer.start_filter()
---> 71     return draw(artist, renderer)
     72 finally:
     73     if artist.get_agg_filter() is not None:

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/axes/_base.py:3226, in _AxesBase.draw(self, renderer)
   3223 if artists_rasterized:
   3224     _draw_rasterized(self.get_figure(root=True), artists_rasterized, renderer)
-> 3226 mimage._draw_list_compositing_images(
   3227     renderer, self, artists, self.get_figure(root=True).suppressComposite)
   3229 renderer.close_group('axes')
   3230 self.stale = False

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/image.py:134, in _draw_list_compositing_images(renderer, parent, artists, suppress_composite)
    132 if not_composite or not has_images:
    133     for a in artists:
--> 134         a.draw(renderer)
    135 else:
    136     # Composite any adjacent images together
    137     image_group = []

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/artist.py:71, in allow_rasterization.<locals>.draw_wrapper(artist, renderer)
     68     if artist.get_agg_filter() is not None:
     69         renderer.start_filter()
---> 71     return draw(artist, renderer)
     72 finally:
     73     if artist.get_agg_filter() is not None:

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/axis.py:1405, in Axis.draw(self, renderer)
   1402 renderer.open_group(__name__, gid=self.get_gid())
   1404 ticks_to_draw = self._update_ticks()
-> 1405 tlb1, tlb2 = self._get_ticklabel_bboxes(ticks_to_draw, renderer)
   1407 for tick in ticks_to_draw:
   1408     tick.draw(renderer)

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/axis.py:1332, in Axis._get_ticklabel_bboxes(self, ticks, renderer)
   1330 if renderer is None:
   1331     renderer = self.get_figure(root=True)._get_renderer()
-> 1332 return ([tick.label1.get_window_extent(renderer)
   1333          for tick in ticks if tick.label1.get_visible()],
   1334         [tick.label2.get_window_extent(renderer)
   1335          for tick in ticks if tick.label2.get_visible()])

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/axis.py:1332, in <listcomp>(.0)
   1330 if renderer is None:
   1331     renderer = self.get_figure(root=True)._get_renderer()
-> 1332 return ([tick.label1.get_window_extent(renderer)
   1333          for tick in ticks if tick.label1.get_visible()],
   1334         [tick.label2.get_window_extent(renderer)
   1335          for tick in ticks if tick.label2.get_visible()])

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/text.py:969, in Text.get_window_extent(self, renderer, dpi)
    964     raise RuntimeError(
    965         "Cannot get window extent of text w/o renderer. You likely "
    966         "want to call 'figure.draw_without_rendering()' first.")
    968 with cbook._setattr_cm(fig, dpi=dpi):
--> 969     bbox, info, descent = self._get_layout(self._renderer)
    970     x, y = self.get_unitless_position()
    971     x, y = self.get_transform().transform((x, y))

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/text.py:373, in Text._get_layout(self, renderer)
    370 ys = []
    372 # Full vertical extent of font, including ascenders and descenders:
--> 373 _, lp_h, lp_d = _get_text_metrics_with_cache(
    374     renderer, "lp", self._fontproperties,
    375     ismath="TeX" if self.get_usetex() else False,
    376     dpi=self.get_figure(root=True).dpi)
    377 min_dy = (lp_h - lp_d) * self._linespacing
    379 for i, line in enumerate(lines):

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/text.py:69, in _get_text_metrics_with_cache(renderer, text, fontprop, ismath, dpi)
     66 """Call ``renderer.get_text_width_height_descent``, caching the results."""
     67 # Cached based on a copy of fontprop so that later in-place mutations of
     68 # the passed-in argument do not mess up the cache.
---> 69 return _get_text_metrics_with_cache_impl(
     70     weakref.ref(renderer), text, fontprop.copy(), ismath, dpi)

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/text.py:77, in _get_text_metrics_with_cache_impl(renderer_ref, text, fontprop, ismath, dpi)
     73 @functools.lru_cache(4096)
     74 def _get_text_metrics_with_cache_impl(
     75         renderer_ref, text, fontprop, ismath, dpi):
     76     # dpi is unused, but participates in cache invalidation (via the renderer).
---> 77     return renderer_ref().get_text_width_height_descent(text, fontprop, ismath)

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/backends/backend_agg.py:211, in RendererAgg.get_text_width_height_descent(self, s, prop, ismath)
    209 _api.check_in_list(["TeX", True, False], ismath=ismath)
    210 if ismath == "TeX":
--> 211     return super().get_text_width_height_descent(s, prop, ismath)
    213 if ismath:
    214     ox, oy, width, height, descent, font_image = \
    215         self.mathtext_parser.parse(s, self.dpi, prop)

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/backend_bases.py:566, in RendererBase.get_text_width_height_descent(self, s, prop, ismath)
    562 fontsize = prop.get_size_in_points()
    564 if ismath == 'TeX':
    565     # todo: handle properties
--> 566     return self.get_texmanager().get_text_width_height_descent(
    567         s, fontsize, renderer=self)
    569 dpi = self.points_to_pixels(72)
    570 if ismath:

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/texmanager.py:364, in TexManager.get_text_width_height_descent(cls, tex, fontsize, renderer)
    362 if tex.strip() == '':
    363     return 0, 0, 0
--> 364 dvifile = cls.make_dvi(tex, fontsize)
    365 dpi_fraction = renderer.points_to_pixels(1.) if renderer else 1
    366 with dviread.Dvi(dvifile, 72 * dpi_fraction) as dvi:

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/texmanager.py:293, in TexManager.make_dvi(cls, tex, fontsize)
    290 with TemporaryDirectory(dir=dvifile.parent) as tmpdir:
    291     Path(tmpdir, "file.tex").write_text(
    292         cls._get_tex_source(tex, fontsize), encoding='utf-8')
--> 293     cls._run_checked_subprocess(
    294         ["latex", "-interaction=nonstopmode", "-halt-on-error",
    295          "-no-shell-escape", "file.tex"], tex, cwd=tmpdir)
    296     Path(tmpdir, "file.dvi").replace(dvifile)
    297     # Also move the tex source to the main cache directory, but
    298     # only for backcompat.

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/texmanager.py:254, in TexManager._run_checked_subprocess(cls, command, tex, cwd)
    250     report = subprocess.check_output(
    251         command, cwd=cwd if cwd is not None else cls._texcache,
    252         stderr=subprocess.STDOUT)
    253 except FileNotFoundError as exc:
--> 254     raise RuntimeError(
    255         f'Failed to process string with tex because {command[0]} '
    256         'could not be found') from exc
    257 except subprocess.CalledProcessError as exc:
    258     raise RuntimeError(
    259         '{prog} was not able to process the following string:\n'
    260         '{tex!r}\n\n'
   (...)    267             exc=exc.output.decode('utf-8', 'backslashreplace'))
    268         ) from None

RuntimeError: Failed to process string with tex because latex could not be found

<Figure size 640x480 with 1 Axes>

scipy.integrate.newton_cotes

Koeficiente integracijskega pristopa Newton-Cotes pridobimo tudi s pomočjo scipy.integrate.newton_cotes() dokumentacija:

newton_cotes(rn, equal=0)

kjer sta parametra:

• rn, ki definira število podintervalov (mogoč je tudi nekonstanten korak, glejte dokumentacijo),

• equal, ki definira ali se zahteva konstantno široke podintervale.

Funkcija vrne terko, pri čemer prvi element predstavlja numerično polje uteži in drugi člen oceno napake.

Poglejmo si primer:

from scipy import integrate
integrate.newton_cotes(2)

(array([0.33333333, 1.33333333, 0.33333333]), -0.011111111111111112)

Izračun uteži za Simpsonovo 3/8 pravilo

Nadaljujemo lahko s kubično interpolacijo čez štiri točke (\(n=4\)):

x, x0, x1, x2, x3, h = sym.symbols('x, x0, x1, x2, x3, h')
zamenjave = {x1: x0+h, x2: x0+2*h, x3: x0+3*h}
A_Simpson3_8 = [sym.integrate(li, (x, x0, x3)).factor().subs(zamenjave).factor() 
                for li in lagrange(4, x)]
A_Simpson3_8

\[\displaystyle \left[ \frac{3 h}{8}, \ \frac{9 h}{8}, \ \frac{9 h}{8}, \ \frac{3 h}{8}\right]\]

Simpsonovo 3/8 pravilo je:

\[I_{\textrm{Simpsonovo 3/8}}=\frac{3h}{8}\left(y_0+3\,y_1+3\,y_2+y_3\right)\]

Ocena napake je (vir: Burden, Faires, Burden: Numerical Analysis 10th Ed):

\[E_{\textrm{Simpsonovo 3/8}}= -\frac{3\,h^5}{80}f^{(4)}(\xi).\]

Poglejmo si primer uporabe. Uporabimo pripravljeno tabelo vrednosti funkcije v štirih točkah:

y4v

array([0.84147098, 1.2959172 , 1.65901326, 1.81859485])

I_Simps38 = 3*h4v/8 * np.sum(y4v * [1, 3, 3, 1])
I_Simps38

\[\displaystyle 1.44060715408392\]

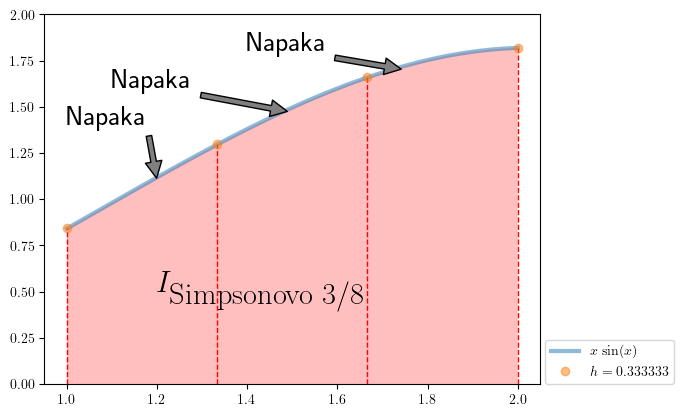
Pripravimo še prikaz:

def fig_Simpsonovo38():
    y_interpolate = interpolate.lagrange(x4v, y4v)
    plt.fill_between(xg, y_interpolate(xg), alpha=0.25, facecolor='r')
    plt.vlines(x4v, 0, y4v, color='r', linestyles='dashed', lw=1)
    plt.annotate('$I_{\\textrm{Simpsonovo 3/8}}$', (1.2, 0.5), fontsize=22)
    plt.annotate('Napaka', fontsize=20, xy=(1.75, 1.7), xytext=(1.4, 1.8),
            arrowprops=dict(facecolor='gray', shrink=0.05))
    plt.annotate('Napaka', fontsize=20, xy=(1.5, 1.47), xytext=(1.1, 1.6),
            arrowprops=dict(facecolor='gray', shrink=0.05))
    plt.annotate('Napaka', fontsize=20, xy=(1.2, 1.1), xytext=(1., 1.4),
            arrowprops=dict(facecolor='gray', shrink=0.05))    
    plt.plot(xg, yg, lw=3, alpha=0.5, label='$x\\,\\sin(x)$')
    plt.plot(x4v, y4v, 'o', alpha=0.5, label=f'$h={h4v:.6f}$')
    plt.legend(loc=(1.01, 0))
    plt.ylim(0, 2)
    plt.show()

Prikažemo:

fig_Simpsonovo38() 

---------------------------------------------------------------------------
FileNotFoundError                         Traceback (most recent call last)
File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/texmanager.py:250, in TexManager._run_checked_subprocess(cls, command, tex, cwd)
    249 try:
--> 250     report = subprocess.check_output(
    251         command, cwd=cwd if cwd is not None else cls._texcache,
    252         stderr=subprocess.STDOUT)
    253 except FileNotFoundError as exc:

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/subprocess.py:466, in check_output(timeout, *popenargs, **kwargs)
    464     kwargs['input'] = empty
--> 466 return run(*popenargs, stdout=PIPE, timeout=timeout, check=True,
    467            **kwargs).stdout

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/subprocess.py:548, in run(input, capture_output, timeout, check, *popenargs, **kwargs)
    546     kwargs['stderr'] = PIPE
--> 548 with Popen(*popenargs, **kwargs) as process:
    549     try:

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/subprocess.py:1026, in Popen.__init__(self, args, bufsize, executable, stdin, stdout, stderr, preexec_fn, close_fds, shell, cwd, env, universal_newlines, startupinfo, creationflags, restore_signals, start_new_session, pass_fds, user, group, extra_groups, encoding, errors, text, umask, pipesize, process_group)
   1023             self.stderr = io.TextIOWrapper(self.stderr,
   1024                     encoding=encoding, errors=errors)
-> 1026     self._execute_child(args, executable, preexec_fn, close_fds,
   1027                         pass_fds, cwd, env,
   1028                         startupinfo, creationflags, shell,
   1029                         p2cread, p2cwrite,
   1030                         c2pread, c2pwrite,
   1031                         errread, errwrite,
   1032                         restore_signals,
   1033                         gid, gids, uid, umask,
   1034                         start_new_session, process_group)
   1035 except:
   1036     # Cleanup if the child failed starting.

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/subprocess.py:1955, in Popen._execute_child(self, args, executable, preexec_fn, close_fds, pass_fds, cwd, env, startupinfo, creationflags, shell, p2cread, p2cwrite, c2pread, c2pwrite, errread, errwrite, restore_signals, gid, gids, uid, umask, start_new_session, process_group)
   1954 if err_filename is not None:
-> 1955     raise child_exception_type(errno_num, err_msg, err_filename)
   1956 else:

FileNotFoundError: [Errno 2] No such file or directory: 'latex'

The above exception was the direct cause of the following exception:

RuntimeError                              Traceback (most recent call last)
File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/backend_bases.py:2157, in FigureCanvasBase.print_figure(self, filename, dpi, facecolor, edgecolor, orientation, format, bbox_inches, pad_inches, bbox_extra_artists, backend, **kwargs)
   2154     # we do this instead of `self.figure.draw_without_rendering`
   2155     # so that we can inject the orientation
   2156     with getattr(renderer, "_draw_disabled", nullcontext)():
-> 2157         self.figure.draw(renderer)
   2158 if bbox_inches:
   2159     if bbox_inches == "tight":

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/artist.py:94, in _finalize_rasterization.<locals>.draw_wrapper(artist, renderer, *args, **kwargs)
     92 @wraps(draw)
     93 def draw_wrapper(artist, renderer, *args, **kwargs):
---> 94     result = draw(artist, renderer, *args, **kwargs)
     95     if renderer._rasterizing:
     96         renderer.stop_rasterizing()

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/artist.py:71, in allow_rasterization.<locals>.draw_wrapper(artist, renderer)
     68     if artist.get_agg_filter() is not None:
     69         renderer.start_filter()
---> 71     return draw(artist, renderer)
     72 finally:
     73     if artist.get_agg_filter() is not None:

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/figure.py:3264, in Figure.draw(self, renderer)
   3261             # ValueError can occur when resizing a window.
   3263     self.patch.draw(renderer)
-> 3264     mimage._draw_list_compositing_images(
   3265         renderer, self, artists, self.suppressComposite)
   3267     renderer.close_group('figure')
   3268 finally:

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/image.py:134, in _draw_list_compositing_images(renderer, parent, artists, suppress_composite)
    132 if not_composite or not has_images:
    133     for a in artists:
--> 134         a.draw(renderer)
    135 else:
    136     # Composite any adjacent images together
    137     image_group = []

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/artist.py:71, in allow_rasterization.<locals>.draw_wrapper(artist, renderer)
     68     if artist.get_agg_filter() is not None:
     69         renderer.start_filter()
---> 71     return draw(artist, renderer)
     72 finally:
     73     if artist.get_agg_filter() is not None:

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/axes/_base.py:3226, in _AxesBase.draw(self, renderer)
   3223 if artists_rasterized:
   3224     _draw_rasterized(self.get_figure(root=True), artists_rasterized, renderer)
-> 3226 mimage._draw_list_compositing_images(
   3227     renderer, self, artists, self.get_figure(root=True).suppressComposite)
   3229 renderer.close_group('axes')
   3230 self.stale = False

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/image.py:134, in _draw_list_compositing_images(renderer, parent, artists, suppress_composite)
    132 if not_composite or not has_images:
    133     for a in artists:
--> 134         a.draw(renderer)
    135 else:
    136     # Composite any adjacent images together
    137     image_group = []

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/artist.py:71, in allow_rasterization.<locals>.draw_wrapper(artist, renderer)
     68     if artist.get_agg_filter() is not None:
     69         renderer.start_filter()
---> 71     return draw(artist, renderer)
     72 finally:
     73     if artist.get_agg_filter() is not None:

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/axis.py:1405, in Axis.draw(self, renderer)
   1402 renderer.open_group(__name__, gid=self.get_gid())
   1404 ticks_to_draw = self._update_ticks()
-> 1405 tlb1, tlb2 = self._get_ticklabel_bboxes(ticks_to_draw, renderer)
   1407 for tick in ticks_to_draw:
   1408     tick.draw(renderer)

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/axis.py:1332, in Axis._get_ticklabel_bboxes(self, ticks, renderer)
   1330 if renderer is None:
   1331     renderer = self.get_figure(root=True)._get_renderer()
-> 1332 return ([tick.label1.get_window_extent(renderer)
   1333          for tick in ticks if tick.label1.get_visible()],
   1334         [tick.label2.get_window_extent(renderer)
   1335          for tick in ticks if tick.label2.get_visible()])

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/axis.py:1332, in <listcomp>(.0)
   1330 if renderer is None:
   1331     renderer = self.get_figure(root=True)._get_renderer()
-> 1332 return ([tick.label1.get_window_extent(renderer)
   1333          for tick in ticks if tick.label1.get_visible()],
   1334         [tick.label2.get_window_extent(renderer)
   1335          for tick in ticks if tick.label2.get_visible()])

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/text.py:969, in Text.get_window_extent(self, renderer, dpi)
    964     raise RuntimeError(
    965         "Cannot get window extent of text w/o renderer. You likely "
    966         "want to call 'figure.draw_without_rendering()' first.")
    968 with cbook._setattr_cm(fig, dpi=dpi):
--> 969     bbox, info, descent = self._get_layout(self._renderer)
    970     x, y = self.get_unitless_position()
    971     x, y = self.get_transform().transform((x, y))

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/text.py:373, in Text._get_layout(self, renderer)
    370 ys = []
    372 # Full vertical extent of font, including ascenders and descenders:
--> 373 _, lp_h, lp_d = _get_text_metrics_with_cache(
    374     renderer, "lp", self._fontproperties,
    375     ismath="TeX" if self.get_usetex() else False,
    376     dpi=self.get_figure(root=True).dpi)
    377 min_dy = (lp_h - lp_d) * self._linespacing
    379 for i, line in enumerate(lines):

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/text.py:69, in _get_text_metrics_with_cache(renderer, text, fontprop, ismath, dpi)
     66 """Call ``renderer.get_text_width_height_descent``, caching the results."""
     67 # Cached based on a copy of fontprop so that later in-place mutations of
     68 # the passed-in argument do not mess up the cache.
---> 69 return _get_text_metrics_with_cache_impl(
     70     weakref.ref(renderer), text, fontprop.copy(), ismath, dpi)

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/text.py:77, in _get_text_metrics_with_cache_impl(renderer_ref, text, fontprop, ismath, dpi)
     73 @functools.lru_cache(4096)
     74 def _get_text_metrics_with_cache_impl(
     75         renderer_ref, text, fontprop, ismath, dpi):
     76     # dpi is unused, but participates in cache invalidation (via the renderer).
---> 77     return renderer_ref().get_text_width_height_descent(text, fontprop, ismath)

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/backends/backend_agg.py:211, in RendererAgg.get_text_width_height_descent(self, s, prop, ismath)
    209 _api.check_in_list(["TeX", True, False], ismath=ismath)
    210 if ismath == "TeX":
--> 211     return super().get_text_width_height_descent(s, prop, ismath)
    213 if ismath:
    214     ox, oy, width, height, descent, font_image = \
    215         self.mathtext_parser.parse(s, self.dpi, prop)

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/backend_bases.py:566, in RendererBase.get_text_width_height_descent(self, s, prop, ismath)
    562 fontsize = prop.get_size_in_points()
    564 if ismath == 'TeX':
    565     # todo: handle properties
--> 566     return self.get_texmanager().get_text_width_height_descent(
    567         s, fontsize, renderer=self)
    569 dpi = self.points_to_pixels(72)
    570 if ismath:

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/texmanager.py:364, in TexManager.get_text_width_height_descent(cls, tex, fontsize, renderer)
    362 if tex.strip() == '':
    363     return 0, 0, 0
--> 364 dvifile = cls.make_dvi(tex, fontsize)
    365 dpi_fraction = renderer.points_to_pixels(1.) if renderer else 1
    366 with dviread.Dvi(dvifile, 72 * dpi_fraction) as dvi:

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/texmanager.py:293, in TexManager.make_dvi(cls, tex, fontsize)
    290 with TemporaryDirectory(dir=dvifile.parent) as tmpdir:
    291     Path(tmpdir, "file.tex").write_text(
    292         cls._get_tex_source(tex, fontsize), encoding='utf-8')
--> 293     cls._run_checked_subprocess(
    294         ["latex", "-interaction=nonstopmode", "-halt-on-error",
    295          "-no-shell-escape", "file.tex"], tex, cwd=tmpdir)
    296     Path(tmpdir, "file.dvi").replace(dvifile)
    297     # Also move the tex source to the main cache directory, but
    298     # only for backcompat.

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/texmanager.py:254, in TexManager._run_checked_subprocess(cls, command, tex, cwd)
    250     report = subprocess.check_output(
    251         command, cwd=cwd if cwd is not None else cls._texcache,
    252         stderr=subprocess.STDOUT)
    253 except FileNotFoundError as exc:
--> 254     raise RuntimeError(
    255         f'Failed to process string with tex because {command[0]} '
    256         'could not be found') from exc
    257 except subprocess.CalledProcessError as exc:
    258     raise RuntimeError(
    259         '{prog} was not able to process the following string:\n'
    260         '{tex!r}\n\n'
   (...)    267             exc=exc.output.decode('utf-8', 'backslashreplace'))
    268         ) from None

RuntimeError: Failed to process string with tex because latex could not be found

<Figure size 640x480 with 1 Axes>

Sestavljeno Simpsonovo pravilo

Interval \([a, b]\) razdelimo na sodo število \(n\) podintervalov enake širine \(h=(b - a)/n\), s čimer so definirana vozlišča \(x_i=a+i\,h\) za \(i=0,1,\dots,n\). V tem primeru zapišemo sestavljeno Simpsonovo pravilo:

\[\int_{a}^{b}f(x)\,\textrm{d}x= \frac{h}{3}\left( f(x_0) +4\sum_{i=1}^{n/2}f(x_{2i-1}) +2\sum_{i=1}^{n/2-1}f(x_{2i}) +f(x_n) \right) \underbrace{ -\frac{b-a}{180}h^4\,f^{(4)}(\eta) }_{E_{\textrm{Sestavljeno Simpsonovo 1/3}}} ,\]

kjer je \(\eta\) neznana vrednost na intervalu \([a, b]\). Napaka je četrtega reda \(\mathcal{O}(h^4)\).

Numerična implementacija:

def simpsonovo_sest(y, h):
    """
    Sestavljeno Simpsonovo pravilo integriranja.

    :param y: funkcijske vrednosti
    :param h: korak integriranja
    """    
    return h/3 * (y[0] + 4*np.sum(y[1:-1:2]) + 2*np.sum(y[2:-1:2]) + y[-1])

I_Simps_sest = simpsonovo_sest(y5v, h=h5v)
I_Simps_sest

\[\displaystyle 1.44044796026391\]

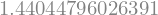
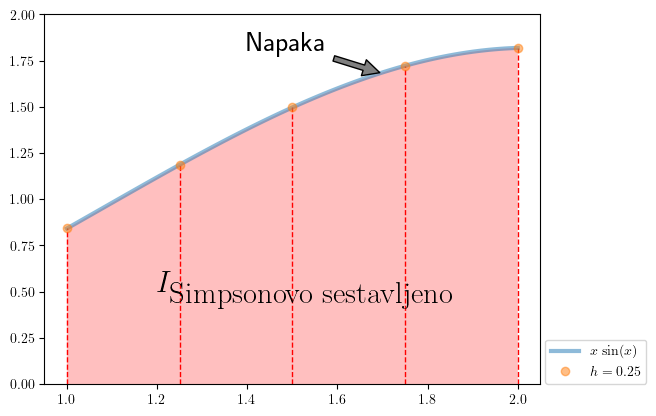
Pripravimo sliko:

def fig_Simpsonovo_sest():
    y_interpolate = interpolate.lagrange(x5v, y5v)
    plt.fill_between(xg, y_interpolate(xg), alpha=0.25, facecolor='r')       
    plt.vlines(x5v, 0, y5v, color='r', linestyles='dashed', lw=1)
    plt.annotate('$I_{\\textrm{Simpsonovo sestavljeno}}$', (1.2, 0.5), fontsize=22)
    plt.annotate('Napaka', fontsize=20, xy=(1.70, 1.68), xytext=(1.4, 1.8),
            arrowprops=dict(facecolor='gray', shrink=0.05))
    plt.plot(xg, yg, lw=3, alpha=0.5, label='$x\\,\\sin(x)$')
    plt.plot(x5v, y5v, 'o', alpha=0.5, label=f'$h={h5v}$')
    plt.legend(loc=(1.01, 0))
    plt.ylim(0, 2)
    plt.show()

Prikažemo:

fig_Simpsonovo_sest()

---------------------------------------------------------------------------
FileNotFoundError                         Traceback (most recent call last)
File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/texmanager.py:250, in TexManager._run_checked_subprocess(cls, command, tex, cwd)
    249 try:
--> 250     report = subprocess.check_output(
    251         command, cwd=cwd if cwd is not None else cls._texcache,
    252         stderr=subprocess.STDOUT)
    253 except FileNotFoundError as exc:

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/subprocess.py:466, in check_output(timeout, *popenargs, **kwargs)
    464     kwargs['input'] = empty
--> 466 return run(*popenargs, stdout=PIPE, timeout=timeout, check=True,
    467            **kwargs).stdout

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/subprocess.py:548, in run(input, capture_output, timeout, check, *popenargs, **kwargs)
    546     kwargs['stderr'] = PIPE
--> 548 with Popen(*popenargs, **kwargs) as process:
    549     try:

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/subprocess.py:1026, in Popen.__init__(self, args, bufsize, executable, stdin, stdout, stderr, preexec_fn, close_fds, shell, cwd, env, universal_newlines, startupinfo, creationflags, restore_signals, start_new_session, pass_fds, user, group, extra_groups, encoding, errors, text, umask, pipesize, process_group)
   1023             self.stderr = io.TextIOWrapper(self.stderr,
   1024                     encoding=encoding, errors=errors)
-> 1026     self._execute_child(args, executable, preexec_fn, close_fds,
   1027                         pass_fds, cwd, env,
   1028                         startupinfo, creationflags, shell,
   1029                         p2cread, p2cwrite,
   1030                         c2pread, c2pwrite,
   1031                         errread, errwrite,
   1032                         restore_signals,
   1033                         gid, gids, uid, umask,
   1034                         start_new_session, process_group)
   1035 except:
   1036     # Cleanup if the child failed starting.

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/subprocess.py:1955, in Popen._execute_child(self, args, executable, preexec_fn, close_fds, pass_fds, cwd, env, startupinfo, creationflags, shell, p2cread, p2cwrite, c2pread, c2pwrite, errread, errwrite, restore_signals, gid, gids, uid, umask, start_new_session, process_group)
   1954 if err_filename is not None:
-> 1955     raise child_exception_type(errno_num, err_msg, err_filename)
   1956 else:

FileNotFoundError: [Errno 2] No such file or directory: 'latex'

The above exception was the direct cause of the following exception:

RuntimeError                              Traceback (most recent call last)
File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/backend_bases.py:2157, in FigureCanvasBase.print_figure(self, filename, dpi, facecolor, edgecolor, orientation, format, bbox_inches, pad_inches, bbox_extra_artists, backend, **kwargs)
   2154     # we do this instead of `self.figure.draw_without_rendering`
   2155     # so that we can inject the orientation
   2156     with getattr(renderer, "_draw_disabled", nullcontext)():
-> 2157         self.figure.draw(renderer)
   2158 if bbox_inches:
   2159     if bbox_inches == "tight":

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/artist.py:94, in _finalize_rasterization.<locals>.draw_wrapper(artist, renderer, *args, **kwargs)
     92 @wraps(draw)
     93 def draw_wrapper(artist, renderer, *args, **kwargs):
---> 94     result = draw(artist, renderer, *args, **kwargs)
     95     if renderer._rasterizing:
     96         renderer.stop_rasterizing()

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/artist.py:71, in allow_rasterization.<locals>.draw_wrapper(artist, renderer)
     68     if artist.get_agg_filter() is not None:
     69         renderer.start_filter()
---> 71     return draw(artist, renderer)
     72 finally:
     73     if artist.get_agg_filter() is not None:

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/figure.py:3264, in Figure.draw(self, renderer)
   3261             # ValueError can occur when resizing a window.
   3263     self.patch.draw(renderer)
-> 3264     mimage._draw_list_compositing_images(
   3265         renderer, self, artists, self.suppressComposite)
   3267     renderer.close_group('figure')
   3268 finally:

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/image.py:134, in _draw_list_compositing_images(renderer, parent, artists, suppress_composite)
    132 if not_composite or not has_images:
    133     for a in artists:
--> 134         a.draw(renderer)
    135 else:
    136     # Composite any adjacent images together
    137     image_group = []

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/artist.py:71, in allow_rasterization.<locals>.draw_wrapper(artist, renderer)
     68     if artist.get_agg_filter() is not None:
     69         renderer.start_filter()
---> 71     return draw(artist, renderer)
     72 finally:
     73     if artist.get_agg_filter() is not None:

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/axes/_base.py:3226, in _AxesBase.draw(self, renderer)
   3223 if artists_rasterized:
   3224     _draw_rasterized(self.get_figure(root=True), artists_rasterized, renderer)
-> 3226 mimage._draw_list_compositing_images(
   3227     renderer, self, artists, self.get_figure(root=True).suppressComposite)
   3229 renderer.close_group('axes')
   3230 self.stale = False

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/image.py:134, in _draw_list_compositing_images(renderer, parent, artists, suppress_composite)
    132 if not_composite or not has_images:
    133     for a in artists:
--> 134         a.draw(renderer)
    135 else:
    136     # Composite any adjacent images together
    137     image_group = []

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/artist.py:71, in allow_rasterization.<locals>.draw_wrapper(artist, renderer)
     68     if artist.get_agg_filter() is not None:
     69         renderer.start_filter()
---> 71     return draw(artist, renderer)
     72 finally:
     73     if artist.get_agg_filter() is not None:

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/axis.py:1405, in Axis.draw(self, renderer)
   1402 renderer.open_group(__name__, gid=self.get_gid())
   1404 ticks_to_draw = self._update_ticks()
-> 1405 tlb1, tlb2 = self._get_ticklabel_bboxes(ticks_to_draw, renderer)
   1407 for tick in ticks_to_draw:
   1408     tick.draw(renderer)

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/axis.py:1332, in Axis._get_ticklabel_bboxes(self, ticks, renderer)
   1330 if renderer is None:
   1331     renderer = self.get_figure(root=True)._get_renderer()
-> 1332 return ([tick.label1.get_window_extent(renderer)
   1333          for tick in ticks if tick.label1.get_visible()],
   1334         [tick.label2.get_window_extent(renderer)
   1335          for tick in ticks if tick.label2.get_visible()])

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/axis.py:1332, in <listcomp>(.0)
   1330 if renderer is None:
   1331     renderer = self.get_figure(root=True)._get_renderer()
-> 1332 return ([tick.label1.get_window_extent(renderer)
   1333          for tick in ticks if tick.label1.get_visible()],
   1334         [tick.label2.get_window_extent(renderer)
   1335          for tick in ticks if tick.label2.get_visible()])

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/text.py:969, in Text.get_window_extent(self, renderer, dpi)
    964     raise RuntimeError(
    965         "Cannot get window extent of text w/o renderer. You likely "
    966         "want to call 'figure.draw_without_rendering()' first.")
    968 with cbook._setattr_cm(fig, dpi=dpi):
--> 969     bbox, info, descent = self._get_layout(self._renderer)
    970     x, y = self.get_unitless_position()
    971     x, y = self.get_transform().transform((x, y))

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/text.py:373, in Text._get_layout(self, renderer)
    370 ys = []
    372 # Full vertical extent of font, including ascenders and descenders:
--> 373 _, lp_h, lp_d = _get_text_metrics_with_cache(
    374     renderer, "lp", self._fontproperties,
    375     ismath="TeX" if self.get_usetex() else False,
    376     dpi=self.get_figure(root=True).dpi)
    377 min_dy = (lp_h - lp_d) * self._linespacing
    379 for i, line in enumerate(lines):

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/text.py:69, in _get_text_metrics_with_cache(renderer, text, fontprop, ismath, dpi)
     66 """Call ``renderer.get_text_width_height_descent``, caching the results."""
     67 # Cached based on a copy of fontprop so that later in-place mutations of
     68 # the passed-in argument do not mess up the cache.
---> 69 return _get_text_metrics_with_cache_impl(
     70     weakref.ref(renderer), text, fontprop.copy(), ismath, dpi)

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/text.py:77, in _get_text_metrics_with_cache_impl(renderer_ref, text, fontprop, ismath, dpi)
     73 @functools.lru_cache(4096)
     74 def _get_text_metrics_with_cache_impl(
     75         renderer_ref, text, fontprop, ismath, dpi):
     76     # dpi is unused, but participates in cache invalidation (via the renderer).
---> 77     return renderer_ref().get_text_width_height_descent(text, fontprop, ismath)

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/backends/backend_agg.py:211, in RendererAgg.get_text_width_height_descent(self, s, prop, ismath)
    209 _api.check_in_list(["TeX", True, False], ismath=ismath)
    210 if ismath == "TeX":
--> 211     return super().get_text_width_height_descent(s, prop, ismath)
    213 if ismath:
    214     ox, oy, width, height, descent, font_image = \
    215         self.mathtext_parser.parse(s, self.dpi, prop)

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/backend_bases.py:566, in RendererBase.get_text_width_height_descent(self, s, prop, ismath)
    562 fontsize = prop.get_size_in_points()
    564 if ismath == 'TeX':
    565     # todo: handle properties
--> 566     return self.get_texmanager().get_text_width_height_descent(
    567         s, fontsize, renderer=self)
    569 dpi = self.points_to_pixels(72)
    570 if ismath:

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/texmanager.py:364, in TexManager.get_text_width_height_descent(cls, tex, fontsize, renderer)
    362 if tex.strip() == '':
    363     return 0, 0, 0
--> 364 dvifile = cls.make_dvi(tex, fontsize)
    365 dpi_fraction = renderer.points_to_pixels(1.) if renderer else 1
    366 with dviread.Dvi(dvifile, 72 * dpi_fraction) as dvi:

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/texmanager.py:293, in TexManager.make_dvi(cls, tex, fontsize)
    290 with TemporaryDirectory(dir=dvifile.parent) as tmpdir:
    291     Path(tmpdir, "file.tex").write_text(
    292         cls._get_tex_source(tex, fontsize), encoding='utf-8')
--> 293     cls._run_checked_subprocess(
    294         ["latex", "-interaction=nonstopmode", "-halt-on-error",
    295          "-no-shell-escape", "file.tex"], tex, cwd=tmpdir)
    296     Path(tmpdir, "file.dvi").replace(dvifile)
    297     # Also move the tex source to the main cache directory, but
    298     # only for backcompat.

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/texmanager.py:254, in TexManager._run_checked_subprocess(cls, command, tex, cwd)
    250     report = subprocess.check_output(
    251         command, cwd=cwd if cwd is not None else cls._texcache,
    252         stderr=subprocess.STDOUT)
    253 except FileNotFoundError as exc:
--> 254     raise RuntimeError(
    255         f'Failed to process string with tex because {command[0]} '
    256         'could not be found') from exc
    257 except subprocess.CalledProcessError as exc:
    258     raise RuntimeError(
    259         '{prog} was not able to process the following string:\n'
    260         '{tex!r}\n\n'
   (...)    267             exc=exc.output.decode('utf-8', 'backslashreplace'))
    268         ) from None

RuntimeError: Failed to process string with tex because latex could not be found

<Figure size 640x480 with 1 Axes>

Boljša ocena integrala

Napaka sestavljene Simpsonove metode je definirana z:

\[E_{\textrm{Sestavljeno Simpsonovo 1/3}}= -\frac{b-a}{180}h^4\,f^{(4)}(\eta),\]

kjer je \(\eta\) neznana vrednost na intervalu \([a, b]\).

Izboljšano oceno integrala določimo na podoben način kakor pri sestavljeni trapezni metodi; integral \(I\) ocenjujemo pri dveh različnih korakih \(h\) in \(2\,h\), velja natančno:

\[\int_a^b f(x)\,\textrm{d}x = I_h + E_h = I_{2h} + E_{2h},\]

kjer je \(I_h\) približek integrala s korakom \(h\) in \(E_h\) ocena napake pri koraku \(h\); analogno velja za \(I_{2h}\) in \(E_{2h}\).

Če predpostavimo, da je \(f^{(4)}\left (\eta \right )\) v obeh primerih enak, lahko določimo razliko \(I_{2h}-I_{h} = E_{h}-E_{2h}\).

Naprej zapišemo:

\[E_h=-\frac{b-a}{180}h^4\,f^{(4)}(\eta)=h^4\,K.\]

Ob predpostavki, da je \(f^{(4)}\left (\eta \right )\) pri koraku \(h\) in \(2h\) enak (\(\eta\) je pri koraku \(h\) in \(2h\) dejansko različen), zapišemo:

\[E_{2h}=-\frac{(b-a)}{180}(2h)^4\,f^{(4)}(\eta)=16\,h^4\,K\]

Sledi:

\[I_{2h}-I_h=-15K\,h^4.\]

Sedaj lahko ocenimo napako pri koraku \(h\):

\[E_h=h^4\,K=\frac{I_h-I_{2h}}{15}.\]

Na podlagi ocene napake lahko izračunamo boljši približek \(I_{h}^*\):

\[I_h^* = I_h + \frac{1}{15}\,(I_{h}-I_{2h})\]

ali

\[I_h^* = \frac{16}{15}\,I_h - \frac{1}{15}\,I_{2h}\]

Numerični zgled

Predhodno smo s Simpsonovim pravilom že izračunali integral pri koraku \(h=0,5\) in pri koraku \(h=0,25\), rezultata sta bila:

[I_Simps, I_Simps_sest]

\[\displaystyle \left[ 1.44083929301393, \ 1.44044796026391\right]\]

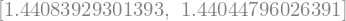
S pomočjo zgornje formule izračunamo boljši približek:

I_Simps_boljši = 16/15*I_Simps_sest - 1/15*I_Simps
print(f'Točen rezultat:   {I_točno}\nBoljši približek: {I_Simps_boljši}')

Točen rezultat:   1.4404224209802097
Boljši približek: 1.4404218714139077

Pridobimo boljši numerični približek, izgubimo pa oceno napake!

Simpsonova metoda v scipy.integrate.simps

V scipy je implementirano sestavljeno Simpsonovo pravilo v scipy.integrate.simpson() (dokumentacija):

simpson(y, x=None, dx=1, axis=-1, even='avg')

kjer so parametri:

• y tabela funkcijskih vrednosti, ki jih integriramo,

• x vozlišča, gre za opcijski parameter, če je x=None, se predpostavi ekvidistantne podintervale širine dx,

• dx širina ekvidistantnih podintervalov oz korak integriranja,

• axis os integriranja (pomembno v primeru večdimenzijskega numeričnega polja)

• even je lahko {'avg', 'first', 'last'} in definira način integriranja v primeru lihega števila podintervalov.

Poglejmo si primer, najprej uvozimo funkcijo simpson:

from scipy.integrate import simpson

#%%timeit
simpson(y5v, dx=h5v)

\[\displaystyle 1.44044796026391\]

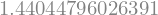
Rombergova metoda

Rombergova metoda temelji na Richardsonovi ekstrapolaciji. Predpostavimo, da integral \(\int_a^b f(x)\textrm{d}x\) integriramo na intervalu \([a,b]\), ki ga razdelimo na \(2^{n-1}\) podintervalov (\(n=1,2,4,8, \dots\)).

Rezultat trapeznega pravila pri \(n=1\) označimo z \(R_{\underbrace{1}_{n},\underbrace{1}_{j}}\), pri čemer \(j\) označuje natančnost pridobljenega rezultata \(\mathcal{O}(h^{2j})\).

Če uporabimo trapezno integracijsko pravilo pri \(n=1,2,4 \dots\) podintervalih, izračunamo:

• \(R_{1,1}\), korak \(h_1=h\), red natančnosti \(\mathcal{O}(h_1^2)\),

• \(R_{2,1}\), korak \(h_2=h/2\), red natančnosti \(\mathcal{O}(h_2^2)\),

• \(R_{3,1}\), korak \(h_3=h/4\), red natančnosti \(\mathcal{O}(h_3^2)\),

• \(R_{4,1}\), korak \(h_4=h/8\), red natančnosti \(\mathcal{O}(h_4^2)\),

• \(\dots\)

• \(R_{n,1}\), korak \(h_4=h/(2^{n-1})\), red natančnosti \(\mathcal{O}(h_n^2)\).

Na podlagi Richardsonove ekstrapolacije izračunamo boljši približek

• \(R_{2,2} = R_{2,1} + \frac{1}{3}\left(R_{2,1}-R_{1,1}\right)\), korak \(h_2=h/2\), red natančnosti \(\mathcal{O}(h_2^4)\),

• \(R_{3,2} = R_{3,1} + \frac{1}{3}\left(R_{3,1}-R_{2,1}\right)\), korak \(h_3=h/4\), red natančnosti \(\mathcal{O}(h_3^4)\),

• \(\dots\)

• \(R_{n,2} = R_{n,1} + \frac{1}{3}\left(R_{n,1}-R_{n-1,1}\right)\), korak \(h_n=h/(2^{n-1})\), red natančnosti \(\mathcal{O}(h_n^4)\).

Nato nadaljujemo z Richardsonovo ekstrapolacijo:

• \(R_{3,3} = R_{3,2} + \frac{1}{15}\left(R_{3,2}-R_{2,2}\right)\), korak \(h_3=h/4\), red natančnosti \(\mathcal{O}(h_3^6)\),

• \(\dots\)

• \(R_{n,3} = R_{n,2} + \frac{1}{15}\left(R_{n,2}-R_{n-1,2}\right)\), korak \(h_n=h/(2^{n-1})\), red natančnosti \(\mathcal{O}(h_n^6)\).

Richardsonovo extrapolacijo lahko posplošimo:

• \(R_{n,j} = R_{n,j-1} + \frac{1}{4^{j-1}-1}\left(R_{n,j-1}-R_{n-1,j-1}\right)\), korak \(h_n=h/(2^{n-1})\), red natančnosti \(\mathcal{O}(h_n^{2j})\)

Pri tem je boljši približek \(R_{2,2}\) pri koraku \(h/2\) enak rezultatu, ki ga dobimo po Simpsonovi metodi pri koraku \(h/2\). Podobno je boljši približek \(R_{3,2}\) pri koraku \(h/4\) enak numeričnemu integralu Simpsonove metode pri koraku \(h/4\). In je dalje \(R_{3,3}\) enak popravljenemu približku Simpsonove metode pri koraku \(h/4\).

Pripravimo numerične podatke:

x9v, h9v = np.linspace(1, 2, 9, retstep=True)  # korak h9v = 0.125 (9 vozlišč)
y9v = x9v * np.sin(x9v)

Poglejmo si primer od zgoraj. Najprej s sestavljeno trapezno metodo izračunamo integral pri različnih korakih (drugi red napake):

## O(h^2)
R1_1 = trapezno_sest(y9v[::8], 8*h9v) # h=1.0
R2_1 = trapezno_sest(y9v[::4], 4*h9v) # h=0.5
R3_1 = trapezno_sest(y9v[::2], 2*h9v) # h=0.25
R4_1 = trapezno_sest(y9v, h9v) # h=0.125
[R1_1, R2_1, R3_1, R4_1]

\[\displaystyle \left[ 1.33003291922963, \ 1.41313769956786, \ 1.4336203950899, \ 1.43872310575291\right]\]

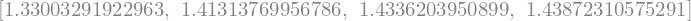
Nato izračunamo boljše približke (dobimo četrti red napake):

## O(h^4)
R2_2 = R2_1 + 1/3 * (R2_1 - R1_1)
R3_2 = R3_1 + 1/3 * (R3_1 - R2_1)
R4_2 = R4_1 + 1/3 * (R4_1 - R3_1)
[R2_2, R3_2, R4_2]

\[\displaystyle \left[ 1.44083929301393, \ 1.44044796026391, \ 1.44042400930725\right]\]

Rezultati predstavljajo rezultat Simpsonove metode pri koraku \(h=0,5\), \(h=0,25\) in \(h=0.125\):

[simpsonovo_sest(y9v[::4], 4*h9v), simpsonovo_sest(y9v[::2], 2*h9v), simpsonovo_sest(y9v, h9v)]

\[\displaystyle \left[ 1.44083929301393, \ 1.44044796026391, \ 1.44042400930725\right]\]

Ponovno izračunamo boljše približke (dobimo šesti red napake):

## O(h6)
R3_3 = R3_2 + 1/15 * (R3_2 - R2_2)
R4_3 = R4_2 + 1/15 * (R4_2 - R3_2)

[R3_3, R4_3]

\[\displaystyle \left[ 1.44042187141391, \ 1.44042241257681\right]\]

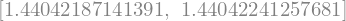
Rezultat predstavlja boljši rezultat Simpsonove pri koraku \(h=0,25\) in \(h=0.125\):

a4h, a2h, ah = [simpsonovo_sest(y9v[::4], 4*h9v), simpsonovo_sest(y9v[::2], 2*h9v), simpsonovo_sest(y9v, h9v)]
[16/15*a2h-1/15*a4h, 16/15*ah-1/15*a2h]

\[\displaystyle \left[ 1.44042187141391, \ 1.44042241257681\right]\]

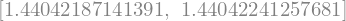
Ponovno izračunamo boljše približke (dobimo osmi red napake):

## O(h8)
R4_4 = R4_3 + 1/63 * (R4_3 - R3_3)
R4_4

\[\displaystyle 1.4404224211667\]

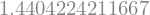
Rombergova metoda nam torej ponuja visoko natančnost rezultata za relativno majhno numerično ceno. Napako pa ocenimo:

\[E = \left|R_{n,n}-R_{n-1,n-1}\right|.\]

Rombergova metoda v scipy.integrate.romb

V scipy je implementirana Rombergova metoda v scipy.integrate.romb() (dokumentacija):

romb(y, dx=1.0, axis=-1, show=False)

kjer so parametri:

• y tabela funkcijskih vrednosti, ki jih integriramo,

• dx širina ekvidistantnih podintervalov oz korak integriranja,

• axis or integriranja (pomembno v primeru večdimenzijskega numeričnega polja),

• show če je True prikaže elemente Richardsonove ekstrapolacije.

Poglejmo si primer od zgoraj:

from scipy.integrate import romb

y9v

array([0.84147098, 1.01505104, 1.18623077, 1.34872795, 1.49624248,
       1.62261343, 1.72197541, 1.78891084, 1.81859485])

romb(y9v, dx=h9v, show=True)

Richardson Extrapolation Table for Romberg Integration
======================================================
 1.33003 
 1.41314  1.44084 
 1.43362  1.44045  1.44042 
 1.43872  1.44042  1.44042  1.44042 
======================================================

\[\displaystyle 1.4404224211667\]

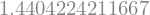
Gaussov integracijski pristop

Newton-Cotesov pristop temelji na polinomu \(n\)-te stopnje in napaka je \(n+1\) stopnje. To pomeni, da integracija daje točen rezultat, če je integrirana funkcija polinom stopnje \(n\) ali manj.

Gaussov integracijski pristop je v principu drugačen: cilj je integral funkcije \(f(x)\) nadomestiti z uteženo vsoto vrednosti funkcije pri diskretnih vrednostih \(f(x_i)\):

\[\int_a^bf(x)\,\textrm{d}x\approx \sum_{i=0}^{n-1} A_i\, f(x_i).\]

Pri tem je neznana utež \(A_i\) in tudi lega vozlišča \(x_i\). Za stopnje polinoma \(n\) bomo potrebovali tudi več točk \((x_i, f(x_i))\).

V nadaljevanju bomo spoznali, da lahko zelo učinkovito izračunamo numerično točen integral. Prednost Gaussove integracije je tudi, da lahko izračuna integral funkcij s singularnostmi (npr: \(\int_0^1\sin(x)/\sqrt{(x)}\,dx\)).

Gaussova kvadratura z enim vozliščem

Predpostavimo, da želimo integrirati polinom stopnje \(n=1\) (linearna funkcija):

\[f(x)=P_1(x)=a_0+a_1\,x.\]

Izračunajmo:

\[\int_{x_L}^{x_D}P_1(x)\,\textrm{d}x=\left(a_0\,x+a_1\,\frac{x^2}{2}\right)_{x_L}^{x_D}=-a_0\,x_L+a_0\,x_D-\frac{a_1\,x_L^2}{2}+\frac{a_1\,x_D^2}{2}.\]

Po drugi strani pa želimo integral izračunati glede na ustrezno uteženo \(A_0\) vrednost funkcije \(f(x_0)\) v neznanem vozlišču \(x_0\) (samo eno vozlišče!):

\[\int_{x_L}^{x_D}P_1(x)\,\textrm{d}x = A_0\,P_1(x_0)= A_0\,a_0+A_0\,a_1\,x_0.\]

Z enačenjem zgornjih izrazov izpeljemo:

\[-a_0\,x_L+a_0\,x_D-\frac{a_1\,x_L^2}{2}+\frac{a_1\,x_D^2}{2}=A_0\,a_0+A_0\,a_1\,x_0.\]

\(a_0\) in \(a_1\) sta koeficienta linearne funkcije, ki lahko zavzame poljubne vrednosti, zato velja:

\[a_0\,\left(-x_L+x_D-A_0\right)=0\qquad\textrm{in}\qquad a_1\left(-\frac{x_L^2}{2}+\frac{x_D^2}{2}-A_0\,x_0\right)=0.\]

Gre za sistem linearnih enačb z rešitvijo:

\[A_0= x_D-x_L, \qquad x_0=\frac{x_L+x_D}{2}.\]

Če je integrirana funkcija linearna, bomo samo na podlagi vrednosti v eni točki izračunali pravo vrednost!

Da je Gaussov integracijski pristop neodvisen od mej integriranja \(x_L\), \(x_D\), pa uvedemo standardne meje.

Standardne meje: \(x_L=-1\) in \(x_D=1\)

Zaradi splošnosti meje \(x\in[x_L, x_D]\) transformiramo v \(\xi\in[-1, +1]\) s pomočjo:

\[x=\frac{x_D+x_L}{2}+\frac{x_D-x_L}{2}\xi\]

in

\[\textrm{d}x=\frac{x_D-x_L}{2}\textrm{d}\xi.\]

Velja:

\[\int_{x_L}^{x_D}f(x)\,\textrm{d}x=\int_{-1}^1 g\left(\xi\right)\,\textrm{d}\xi,\]

kjer je:

\[g(\xi)=\frac{x_D-x_L}{2}\,f\left(\frac{x_L+x_d}{2}+\frac{x_D-x_L}{2}\xi\right).\]

V primeru standardnih mej, je pri eni Gaussovi točki utež \(A_0=2\) in \(x_0=0\) vrednost, pri kateri moramo izračunati funkcijo \(f(x_0)\).

Strojno izpeljevanje uteži in Gaussove točke

Definirajmo simbole in nastavimo enačbo:

a_0, a_1, x, x_L, x_D, A_0, x_0 = sym.symbols('a_0, a_1, x, x_L, x_D, A_0, x_0') # simboli
P1 = a_0 + a_1*x                                                   # linearni polinom
eq = sym.Eq(P1.integrate((x, x_L, x_D)).expand(), A_0*P1.subs(x, x_0)) # teoretični integral = ocen z utežmi
eq

\[\displaystyle a_{0} x_{D} - a_{0} x_{L} + \frac{a_{1} x_{D}^{2}}{2} - \frac{a_{1} x_{L}^{2}}{2} = A_{0} \left(a_{0} + a_{1} x_{0}\right)\]

Pripravimo dve enačbi (za prvo predpostavimo \(a_0=0, a_1=1\), za drugo predpostavimo \(a_0=1, a_1=0\)) ter rešimo sistem za A_0 in x_0:

sym.solve([eq.subs(a_0, 0).subs(a_1, 1), eq.subs(a_1, 0).subs(a_0, 1)], [A_0, x_0])

\[\displaystyle \left[ \left( x_{D} - x_{L}, \ \frac{x_{D} + x_{L}}{2}\right)\right]\]

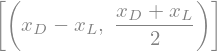
Za dodatno razlago priporočam video posnetek.

Gaussova integracijska metoda z več vozlišči

Izpeljati želimo Gaussovo integracijsko metodo, ki bo upoštevala na intervalu \([a,b]\) \(v\) vozlišč in bo točno izračunala integral polinomov do stopnje \(n=2v-1\). Veljati mora:

\[\int_a^bP_{2v-1}(x)\,\textrm{d}x = \sum_{i=0}^{v-1} A_i\,P_{2v-1}(x_i).\]

Pri izpeljavi se bomo omejili na standardne meje \(x_L=-1\), \(x_D=1\),

kjer je polinom stopnje \(n=2v-1\) definiran kot:

\[P_{2v-1}(x)=\sum_{i=0}^{2v-1} a_i\,x^i.\]

Z dvema Gaussovima točkama/vozliščema točno izračunamo integral polinoma do tretjega reda, s tremi Gaussovimi vozlišči pa točno izračunamo integral polinoma do petega reda!

Strojno izpeljevanje

Pripravimo si najprej simbolni zapis polinoma in ustreznih spremenljivk:

def P_etc(n=1, a='a', x='x'):                       # n je stopnja polinoma
    ai = sym.symbols(f'{a}:{n+1}')                  # seznam a_i
    x = sym.symbols(x)                              # spremenljivka x
    return ai, x, sum([ai[i]*x**i for i in range(n+1)])

Sedaj pa poiščimo uteži \(A_i\) in vozlišča \(x_i\) za primer dveh Gaussovih vozlišč; polinom je torej tretje stopnje.

v = 2 # število vozlišč
ai, x, P = P_etc(n=2*v-1)
xi = sym.symbols(f'x:{v}') # seznam x_i
Ai = sym.symbols(f'A:{v}') # seznam w_i
print(f'Vozlišča: {xi}\nUteži:    {Ai}')

Vozlišča: (x0, x1)
Uteži:    (A0, A1)

Polinom:

P

\[\displaystyle a_{0} + a_{1} x + a_{2} x^{2} + a_{3} x^{3}\]

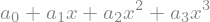
Podobno kakor zgoraj za eno vozlišče, tukaj definirajmo enačbe:

eqs = [sym.Eq(P.integrate((x, -1, 1)).coeff(a_),\
              sum([Ai[i]*P.subs(x, xi[i]) \
                   for i in range(v)]).expand().coeff(a_)) \
       for a_ in ai]
eqs

\[\displaystyle \left[ 2 = A_{0} + A_{1}, \ 0 = A_{0} x_{0} + A_{1} x_{1}, \ \frac{2}{3} = A_{0} x_{0}^{2} + A_{1} x_{1}^{2}, \ 0 = A_{0} x_{0}^{3} + A_{1} x_{1}^{3}\right]\]

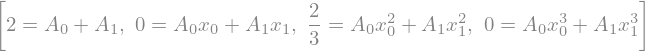
Rešimo jih za neznane \(x_i\) in \(w_i\):

sol = sym.solve(eqs, sym.flatten((xi, Ai)))
sol

\[\displaystyle \left[ \left( - \frac{\sqrt{3}}{3}, \ \frac{\sqrt{3}}{3}, \ 1, \ 1\right), \ \left( \frac{\sqrt{3}}{3}, \ - \frac{\sqrt{3}}{3}, \ 1, \ 1\right)\right]\]

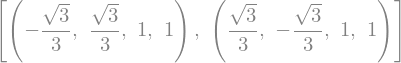
Določili smo seznam dveh (enakih) rešitev.

Najprej sta definirani vozlišči: \(x_0=-\sqrt{3}/3\) in \(x_1=\sqrt{3}/3\), katerima pripadata uteži \(A_0=A_1=1\).

Koda zgoraj je izpeljana v splošnem - število vozlišč v lahko povečate ter izračunate vozlišča ter pripadajoče uteži.

Spodaj je podana tabela vozlišč in uteži za eno, dve in tri vozlišča (za meje \(a=-1\), \(b=1\)):

Število točk 1:

\(i\)	Vozlišče \(x_i\)	Utež \(A_i\)
0	0	2

Število točk 2:

\(i\)	Vozlišče \(x_i\)	Utež \(A_i\)
0	\(-\frac{\sqrt{3}}{3}\)	1
1	\(+\frac{\sqrt{3}}{3}\)	1

Število točk 3:

\(i\)	Vozlišče \(x_i\)	Utež \(A_i\)
0	\(-\frac{\sqrt{15}}{5}\)	\(\frac{5}{9}\)
1	\(0\)	\(\frac{8}{9}\)
2	\(\frac{\sqrt{15}}{5}\)	\(\frac{5}{9}\)

Za več vozlišč in tudi oceno napake, glejte Mathworld Legendre-Gauss Quadrature.

Za primer treh Gaussovih točk numerični integral izračunamo (standardne meje):

\[I_{\textrm{Gauss3}}= \frac{5}{9}\,f\left(-\frac{\sqrt{15}}{5}\right) + \frac{8}{9}\,f\left(0\right)+\frac{5}{9}\,f\left(\frac{\sqrt{15}}{5}\right).\]

Numerična implementacija

Numerična implementacija (vključno s transformacijo mej) za eno, dve ali tri vozlišča:

def Gaussova(fun, a, b, vozlišč=1):
    """ 
    Gaussova integracijska metoda.

    :param fun: objekt funkcije, ki jo integriramo
    :param a:   spodnja meja
    :param b:   zgornja meja
    :param vozlišča: število vozlišč (1, 2 ali 3)
    """
    def g(xi): # funkcija za transformacijo mej
        return (b-a)/2 * fun((b+a +xi * (b-a))/2)
    
    if vozlišč == 1:
        return 2*g(0.)
    elif vozlišč == 2:
        return 1. * g(-np.sqrt(3)/3) + 1. * g(np.sqrt(3)/3)        
    elif vozlišč == 3:
        return 5/9 * g(-np.sqrt(15)/5) +8/9 * g(0.) + 5/9 * g(np.sqrt(15)/5)

Poglejmo si zgled. Najprej definirajmo funkcijo, ki jo želimo integrirati:

def f(x):
    return x*np.sin(x)

Sedaj pa funkcijo (v konkretnem primeru f) in ne vrednosti (npr. f(0.)) posredujemo funkciji Gaussova. Najprej za eno vozlišče, nato dve in tri:

Gaussova(fun=f, a=1., b=2., vozlišč=1)

\[\displaystyle 1.49624247990608\]

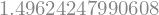
Gaussova(fun=f, a=1., b=2., vozlišč=2)

\[\displaystyle 1.44014401845179\]

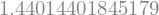
Gaussova(fun=f, a=1., b=2., vozlišč=3)

\[\displaystyle 1.44042294912151\]

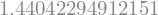
scipy.integrate.fixed_quad

Znotraj scipy je Gaussova integracijska metoda implementirana v okviru funkcije scipy.integrate.fixed_quad() (dokumentacija):

fixed_quad(func, a, b, args=(), n=5)

kjer so parametri:

• func je ime funkcije, ki jo kličemo,

• a je spodnja meja,

• b je zgornja meja,

• args je terka morebitnih dodatnih argumentov funkcije func,

• n je število vozlišč Gaussove integracije, privzeto n=5.

Funkcija vrne terko z rezultatom integriranja val in vrednost None: (val, None)

Poglejmo primer od zgoraj:

from scipy.integrate import fixed_quad
fixed_quad(f, a=1, b=2, n=3)[0]

\[\displaystyle 1.44042294912151\]

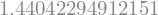
Rezultat je enak predhodnemu:

Gaussova(fun=f, a=1., b=2., vozlišč=3)

\[\displaystyle 1.44042294912151\]

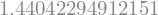
scipy.integrate

scipy.integrate je močno orodje za numerično integriranje (glejte dokumentacijo). V nadaljevanju si bomo pogledali nekatere funkcije.

Intergracijske funkcije, ki zahtevajo definicijsko funkcijo:

• quad(func, a, b[, args, full_output, ...]) izračuna določeni integral func(x) v mejah [a, b],

• dblquad(func, a, b, gfun, hfun[, args, ...]) izračuna določeni integral func(x,y),

• tplquad(func, a, b, gfun, hfun, qfun, rfun) izračuna določeni integral func(x,y,z),

• nquad(func, ranges[, args, opts, full_output]) izračuna določeni integral \(n\) dimenzijske funkcije func( ...),

• romberg(function, a, b[, args, tol, rtol, ...]) integracija Romberg za funkcijo function,

scipy.integrate.quad

Poglejmo si zelo uporabno funkcijo za integriranje, scipy.integrate.quad() (dokumentacija):

quad(func, a, b, args=(), full_output=0, epsabs=1.49e-08, epsrel=1.49e-08, limit=50, 
     points=None, weight=None, wvar=None, wopts=None, maxp1=50, limlst=50)

Izbrani parametri so:

• func Python funkcija, ki jo integriramo,

• a spodnja meja integriranja (lahko se uporabi np.inf za mejo v neskončnosti),

• b zgornja meja integriranja (lahko se uporabi np.inf za mejo v neskončnosti),

• full_output za prikaz vseh rezultatov, privzeto 0,

• epsabs dovoljena absolutna napaka,

• epsrel dovoljena relativna napaka.

Poglejmo primer od zgoraj:

from scipy import integrate

integrate.quad(f, a=1, b=2)

\[\displaystyle \left( 1.44042242098021, \ 1.59919013695854 \cdot 10^{-14}\right)\]

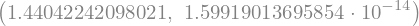
scipy.integrate.dblquad

Gre za podobno funkcijo kot quad, vendar za integriranje po dveh spremenljivkah (dokumentacija). Funkcija scipy.integrate.dblquad() izračuna dvojni integral func(y, x) v mejah od x = [a, b] in y = [gfun(x), hfun(x)].

dblquad(func, a, b, gfun, hfun, args=(), epsabs=1.49e-08, epsrel=1.49e-08)

Izbrani parametri so:

• func je Python funkcija, ki jo integriramo,

• a je spodnja meja integriranja x (lahko se uporabi np.inf za mejo v neskončnosti),

• b je zgornja meja integriranja x (lahko se uporabi np.inf za mejo v neskončnosti),

• gfun je Python funkcija, ki definira spodnjo mejo y v odvisnosti od x,

• hfun je Python funkcija, ki definira zgornjo mejo y v odvisnosti od x.

Poglejmo primer izračuna površine polkroga s polmerom 1:

\[\int_{-1}^{1}\left(\int_0^{\sqrt{1-x^2}}1\,\textrm{d}y\right)\,\textrm{d}x=\frac{\pi}{2}\]

Definirajmo ustrezne Python funkcije in izračunajmo rezultat:

def func(y, x): # integracijska funkcija je enostavna, konstanta = 1!
    return 1.
def gfun(x):    # spodnja meja = 0
    return 0.
def hfun(x):    # zgornja meja
    return np.sqrt(1-x**2)
integrate.dblquad(func=func, a=-1, b=1, gfun=gfun, hfun=hfun)

\[\displaystyle \left( 1.5707963267949, \ 1.00023545002159 \cdot 10^{-9}\right)\]

Intergracijske funkcije, ki zahtevajo tabelo vrednosti:

• trapz(y[, x, dx, axis]) sestavljeno trapezno pravilo,

• cumulative_trapezoid(y[, x, dx, axis, initial]) kumulativni integral podintegralske funkcije (vrne rezultat v vsakem vozlišču),

• simps(y[, x, dx, axis, even]) Simpsonova metoda,

• romb(y[, dx, axis, show]) Rombergova metoda.

Tukaj si bomo na primeru ogledali funkcijo cumulative_trapezoid. Kot primer si, ko na maso \(m=1\) (enote izpustimo) deluje sila \(F=\sin(t)\). Iz 2. Newtonovega zakona sledi: \(F=m\,\ddot x\). Pospešek integriramo, da izračunamo hitrost; nato integriramo še enkrat za pomik. Definirajmo najprej funkcijo za pospešek:

def pospešek(t):
    F = np.sin(t)
    m = 1
    return F/m

Zanima nas dogajanje v času 3 sekund:

t, h = np.linspace(0, 3, 100, retstep=True)

Izračunajmo tabelo pospeškov ter nato integrirajmo za hitrost (pri tem je pomembno, da definiramo začetno vrednost):

a = pospešek(t)
v = integrate.cumulative_trapezoid(y=a, dx=h, initial=0)

Hitrost sedaj še enkrat integrirajmo, da izračunamo pot:

s = integrate.cumulative_trapezoid(y=v, dx=h, initial=0)

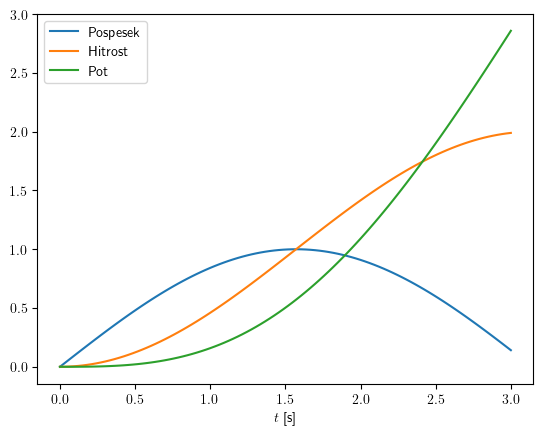
Prikažimo rezultat:

plt.plot(t, a, label='Pospesek')
plt.plot(t, v, label='Hitrost')
plt.plot(t, s, label='Pot')
plt.xlabel('$t$ [s]')
plt.legend();

Error in callback <function _draw_all_if_interactive at 0x7f1ac5885c60> (for post_execute), with arguments args (),kwargs {}:

---------------------------------------------------------------------------
FileNotFoundError                         Traceback (most recent call last)
File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/texmanager.py:250, in TexManager._run_checked_subprocess(cls, command, tex, cwd)
    249 try:
--> 250     report = subprocess.check_output(
    251         command, cwd=cwd if cwd is not None else cls._texcache,
    252         stderr=subprocess.STDOUT)
    253 except FileNotFoundError as exc:

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/subprocess.py:466, in check_output(timeout, *popenargs, **kwargs)
    464     kwargs['input'] = empty
--> 466 return run(*popenargs, stdout=PIPE, timeout=timeout, check=True,
    467            **kwargs).stdout

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/subprocess.py:548, in run(input, capture_output, timeout, check, *popenargs, **kwargs)
    546     kwargs['stderr'] = PIPE
--> 548 with Popen(*popenargs, **kwargs) as process:
    549     try:

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/subprocess.py:1026, in Popen.__init__(self, args, bufsize, executable, stdin, stdout, stderr, preexec_fn, close_fds, shell, cwd, env, universal_newlines, startupinfo, creationflags, restore_signals, start_new_session, pass_fds, user, group, extra_groups, encoding, errors, text, umask, pipesize, process_group)
   1023             self.stderr = io.TextIOWrapper(self.stderr,
   1024                     encoding=encoding, errors=errors)
-> 1026     self._execute_child(args, executable, preexec_fn, close_fds,
   1027                         pass_fds, cwd, env,
   1028                         startupinfo, creationflags, shell,
   1029                         p2cread, p2cwrite,
   1030                         c2pread, c2pwrite,
   1031                         errread, errwrite,
   1032                         restore_signals,
   1033                         gid, gids, uid, umask,
   1034                         start_new_session, process_group)
   1035 except:
   1036     # Cleanup if the child failed starting.

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/subprocess.py:1955, in Popen._execute_child(self, args, executable, preexec_fn, close_fds, pass_fds, cwd, env, startupinfo, creationflags, shell, p2cread, p2cwrite, c2pread, c2pwrite, errread, errwrite, restore_signals, gid, gids, uid, umask, start_new_session, process_group)
   1954 if err_filename is not None:
-> 1955     raise child_exception_type(errno_num, err_msg, err_filename)
   1956 else:

FileNotFoundError: [Errno 2] No such file or directory: 'latex'

The above exception was the direct cause of the following exception:

RuntimeError                              Traceback (most recent call last)
File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/pyplot.py:278, in _draw_all_if_interactive()
    276 def _draw_all_if_interactive() -> None:
    277     if matplotlib.is_interactive():
--> 278         draw_all()

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/_pylab_helpers.py:131, in Gcf.draw_all(cls, force)
    129 for manager in cls.get_all_fig_managers():
    130     if force or manager.canvas.figure.stale:
--> 131         manager.canvas.draw_idle()

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/backend_bases.py:1893, in FigureCanvasBase.draw_idle(self, *args, **kwargs)
   1891 if not self._is_idle_drawing:
   1892     with self._idle_draw_cntx():
-> 1893         self.draw(*args, **kwargs)

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/backends/backend_agg.py:382, in FigureCanvasAgg.draw(self)
    379 # Acquire a lock on the shared font cache.
    380 with (self.toolbar._wait_cursor_for_draw_cm() if self.toolbar
    381       else nullcontext()):
--> 382     self.figure.draw(self.renderer)
    383     # A GUI class may be need to update a window using this draw, so
    384     # don't forget to call the superclass.
    385     super().draw()

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/artist.py:94, in _finalize_rasterization.<locals>.draw_wrapper(artist, renderer, *args, **kwargs)
     92 @wraps(draw)
     93 def draw_wrapper(artist, renderer, *args, **kwargs):
---> 94     result = draw(artist, renderer, *args, **kwargs)
     95     if renderer._rasterizing:
     96         renderer.stop_rasterizing()

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/artist.py:71, in allow_rasterization.<locals>.draw_wrapper(artist, renderer)
     68     if artist.get_agg_filter() is not None:
     69         renderer.start_filter()
---> 71     return draw(artist, renderer)
     72 finally:
     73     if artist.get_agg_filter() is not None:

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/figure.py:3264, in Figure.draw(self, renderer)
   3261             # ValueError can occur when resizing a window.
   3263     self.patch.draw(renderer)
-> 3264     mimage._draw_list_compositing_images(
   3265         renderer, self, artists, self.suppressComposite)
   3267     renderer.close_group('figure')
   3268 finally:

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/image.py:134, in _draw_list_compositing_images(renderer, parent, artists, suppress_composite)
    132 if not_composite or not has_images:
    133     for a in artists:
--> 134         a.draw(renderer)
    135 else:
    136     # Composite any adjacent images together
    137     image_group = []

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/artist.py:71, in allow_rasterization.<locals>.draw_wrapper(artist, renderer)
     68     if artist.get_agg_filter() is not None:
     69         renderer.start_filter()
---> 71     return draw(artist, renderer)
     72 finally:
     73     if artist.get_agg_filter() is not None:

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/axes/_base.py:3226, in _AxesBase.draw(self, renderer)
   3223 if artists_rasterized:
   3224     _draw_rasterized(self.get_figure(root=True), artists_rasterized, renderer)
-> 3226 mimage._draw_list_compositing_images(
   3227     renderer, self, artists, self.get_figure(root=True).suppressComposite)
   3229 renderer.close_group('axes')
   3230 self.stale = False

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/image.py:134, in _draw_list_compositing_images(renderer, parent, artists, suppress_composite)
    132 if not_composite or not has_images:
    133     for a in artists:
--> 134         a.draw(renderer)
    135 else:
    136     # Composite any adjacent images together
    137     image_group = []

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/artist.py:71, in allow_rasterization.<locals>.draw_wrapper(artist, renderer)
     68     if artist.get_agg_filter() is not None:
     69         renderer.start_filter()
---> 71     return draw(artist, renderer)
     72 finally:
     73     if artist.get_agg_filter() is not None:

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/axis.py:1405, in Axis.draw(self, renderer)
   1402 renderer.open_group(__name__, gid=self.get_gid())
   1404 ticks_to_draw = self._update_ticks()
-> 1405 tlb1, tlb2 = self._get_ticklabel_bboxes(ticks_to_draw, renderer)
   1407 for tick in ticks_to_draw:
   1408     tick.draw(renderer)

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/axis.py:1332, in Axis._get_ticklabel_bboxes(self, ticks, renderer)
   1330 if renderer is None:
   1331     renderer = self.get_figure(root=True)._get_renderer()
-> 1332 return ([tick.label1.get_window_extent(renderer)
   1333          for tick in ticks if tick.label1.get_visible()],
   1334         [tick.label2.get_window_extent(renderer)
   1335          for tick in ticks if tick.label2.get_visible()])

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/axis.py:1332, in <listcomp>(.0)
   1330 if renderer is None:
   1331     renderer = self.get_figure(root=True)._get_renderer()
-> 1332 return ([tick.label1.get_window_extent(renderer)
   1333          for tick in ticks if tick.label1.get_visible()],
   1334         [tick.label2.get_window_extent(renderer)
   1335          for tick in ticks if tick.label2.get_visible()])

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/text.py:969, in Text.get_window_extent(self, renderer, dpi)
    964     raise RuntimeError(
    965         "Cannot get window extent of text w/o renderer. You likely "
    966         "want to call 'figure.draw_without_rendering()' first.")
    968 with cbook._setattr_cm(fig, dpi=dpi):
--> 969     bbox, info, descent = self._get_layout(self._renderer)
    970     x, y = self.get_unitless_position()
    971     x, y = self.get_transform().transform((x, y))

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/text.py:373, in Text._get_layout(self, renderer)
    370 ys = []
    372 # Full vertical extent of font, including ascenders and descenders:
--> 373 _, lp_h, lp_d = _get_text_metrics_with_cache(
    374     renderer, "lp", self._fontproperties,
    375     ismath="TeX" if self.get_usetex() else False,
    376     dpi=self.get_figure(root=True).dpi)
    377 min_dy = (lp_h - lp_d) * self._linespacing
    379 for i, line in enumerate(lines):

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/text.py:69, in _get_text_metrics_with_cache(renderer, text, fontprop, ismath, dpi)
     66 """Call ``renderer.get_text_width_height_descent``, caching the results."""
     67 # Cached based on a copy of fontprop so that later in-place mutations of
     68 # the passed-in argument do not mess up the cache.
---> 69 return _get_text_metrics_with_cache_impl(
     70     weakref.ref(renderer), text, fontprop.copy(), ismath, dpi)

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/text.py:77, in _get_text_metrics_with_cache_impl(renderer_ref, text, fontprop, ismath, dpi)
     73 @functools.lru_cache(4096)
     74 def _get_text_metrics_with_cache_impl(
     75         renderer_ref, text, fontprop, ismath, dpi):
     76     # dpi is unused, but participates in cache invalidation (via the renderer).
---> 77     return renderer_ref().get_text_width_height_descent(text, fontprop, ismath)

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/backends/backend_agg.py:211, in RendererAgg.get_text_width_height_descent(self, s, prop, ismath)
    209 _api.check_in_list(["TeX", True, False], ismath=ismath)
    210 if ismath == "TeX":
--> 211     return super().get_text_width_height_descent(s, prop, ismath)
    213 if ismath:
    214     ox, oy, width, height, descent, font_image = \
    215         self.mathtext_parser.parse(s, self.dpi, prop)

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/backend_bases.py:566, in RendererBase.get_text_width_height_descent(self, s, prop, ismath)
    562 fontsize = prop.get_size_in_points()
    564 if ismath == 'TeX':
    565     # todo: handle properties
--> 566     return self.get_texmanager().get_text_width_height_descent(
    567         s, fontsize, renderer=self)
    569 dpi = self.points_to_pixels(72)
    570 if ismath:

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/texmanager.py:364, in TexManager.get_text_width_height_descent(cls, tex, fontsize, renderer)
    362 if tex.strip() == '':
    363     return 0, 0, 0
--> 364 dvifile = cls.make_dvi(tex, fontsize)
    365 dpi_fraction = renderer.points_to_pixels(1.) if renderer else 1
    366 with dviread.Dvi(dvifile, 72 * dpi_fraction) as dvi:

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/texmanager.py:293, in TexManager.make_dvi(cls, tex, fontsize)
    290 with TemporaryDirectory(dir=dvifile.parent) as tmpdir:
    291     Path(tmpdir, "file.tex").write_text(
    292         cls._get_tex_source(tex, fontsize), encoding='utf-8')
--> 293     cls._run_checked_subprocess(
    294         ["latex", "-interaction=nonstopmode", "-halt-on-error",
    295          "-no-shell-escape", "file.tex"], tex, cwd=tmpdir)
    296     Path(tmpdir, "file.dvi").replace(dvifile)
    297     # Also move the tex source to the main cache directory, but
    298     # only for backcompat.

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/texmanager.py:254, in TexManager._run_checked_subprocess(cls, command, tex, cwd)
    250     report = subprocess.check_output(
    251         command, cwd=cwd if cwd is not None else cls._texcache,
    252         stderr=subprocess.STDOUT)
    253 except FileNotFoundError as exc:
--> 254     raise RuntimeError(
    255         f'Failed to process string with tex because {command[0]} '
    256         'could not be found') from exc
    257 except subprocess.CalledProcessError as exc:
    258     raise RuntimeError(
    259         '{prog} was not able to process the following string:\n'
    260         '{tex!r}\n\n'
   (...)    267             exc=exc.output.decode('utf-8', 'backslashreplace'))
    268         ) from None

RuntimeError: Failed to process string with tex because latex could not be found

---------------------------------------------------------------------------
FileNotFoundError                         Traceback (most recent call last)
File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/texmanager.py:250, in TexManager._run_checked_subprocess(cls, command, tex, cwd)
    249 try:
--> 250     report = subprocess.check_output(
    251         command, cwd=cwd if cwd is not None else cls._texcache,
    252         stderr=subprocess.STDOUT)
    253 except FileNotFoundError as exc:

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/subprocess.py:466, in check_output(timeout, *popenargs, **kwargs)
    464     kwargs['input'] = empty
--> 466 return run(*popenargs, stdout=PIPE, timeout=timeout, check=True,
    467            **kwargs).stdout

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/subprocess.py:548, in run(input, capture_output, timeout, check, *popenargs, **kwargs)
    546     kwargs['stderr'] = PIPE
--> 548 with Popen(*popenargs, **kwargs) as process:
    549     try:

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/subprocess.py:1026, in Popen.__init__(self, args, bufsize, executable, stdin, stdout, stderr, preexec_fn, close_fds, shell, cwd, env, universal_newlines, startupinfo, creationflags, restore_signals, start_new_session, pass_fds, user, group, extra_groups, encoding, errors, text, umask, pipesize, process_group)
   1023             self.stderr = io.TextIOWrapper(self.stderr,
   1024                     encoding=encoding, errors=errors)
-> 1026     self._execute_child(args, executable, preexec_fn, close_fds,
   1027                         pass_fds, cwd, env,
   1028                         startupinfo, creationflags, shell,
   1029                         p2cread, p2cwrite,
   1030                         c2pread, c2pwrite,
   1031                         errread, errwrite,
   1032                         restore_signals,
   1033                         gid, gids, uid, umask,
   1034                         start_new_session, process_group)
   1035 except:
   1036     # Cleanup if the child failed starting.

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/subprocess.py:1955, in Popen._execute_child(self, args, executable, preexec_fn, close_fds, pass_fds, cwd, env, startupinfo, creationflags, shell, p2cread, p2cwrite, c2pread, c2pwrite, errread, errwrite, restore_signals, gid, gids, uid, umask, start_new_session, process_group)
   1954 if err_filename is not None:
-> 1955     raise child_exception_type(errno_num, err_msg, err_filename)
   1956 else:

FileNotFoundError: [Errno 2] No such file or directory: 'latex'

The above exception was the direct cause of the following exception:

RuntimeError                              Traceback (most recent call last)
File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/backend_bases.py:2157, in FigureCanvasBase.print_figure(self, filename, dpi, facecolor, edgecolor, orientation, format, bbox_inches, pad_inches, bbox_extra_artists, backend, **kwargs)
   2154     # we do this instead of `self.figure.draw_without_rendering`
   2155     # so that we can inject the orientation
   2156     with getattr(renderer, "_draw_disabled", nullcontext)():
-> 2157         self.figure.draw(renderer)
   2158 if bbox_inches:
   2159     if bbox_inches == "tight":

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/artist.py:94, in _finalize_rasterization.<locals>.draw_wrapper(artist, renderer, *args, **kwargs)
     92 @wraps(draw)
     93 def draw_wrapper(artist, renderer, *args, **kwargs):
---> 94     result = draw(artist, renderer, *args, **kwargs)
     95     if renderer._rasterizing:
     96         renderer.stop_rasterizing()

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/artist.py:71, in allow_rasterization.<locals>.draw_wrapper(artist, renderer)
     68     if artist.get_agg_filter() is not None:
     69         renderer.start_filter()
---> 71     return draw(artist, renderer)
     72 finally:
     73     if artist.get_agg_filter() is not None:

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/figure.py:3264, in Figure.draw(self, renderer)
   3261             # ValueError can occur when resizing a window.
   3263     self.patch.draw(renderer)
-> 3264     mimage._draw_list_compositing_images(
   3265         renderer, self, artists, self.suppressComposite)
   3267     renderer.close_group('figure')
   3268 finally:

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/image.py:134, in _draw_list_compositing_images(renderer, parent, artists, suppress_composite)
    132 if not_composite or not has_images:
    133     for a in artists:
--> 134         a.draw(renderer)
    135 else:
    136     # Composite any adjacent images together
    137     image_group = []

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/artist.py:71, in allow_rasterization.<locals>.draw_wrapper(artist, renderer)
     68     if artist.get_agg_filter() is not None:
     69         renderer.start_filter()
---> 71     return draw(artist, renderer)
     72 finally:
     73     if artist.get_agg_filter() is not None:

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/axes/_base.py:3226, in _AxesBase.draw(self, renderer)
   3223 if artists_rasterized:
   3224     _draw_rasterized(self.get_figure(root=True), artists_rasterized, renderer)
-> 3226 mimage._draw_list_compositing_images(
   3227     renderer, self, artists, self.get_figure(root=True).suppressComposite)
   3229 renderer.close_group('axes')
   3230 self.stale = False

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/image.py:134, in _draw_list_compositing_images(renderer, parent, artists, suppress_composite)
    132 if not_composite or not has_images:
    133     for a in artists:
--> 134         a.draw(renderer)
    135 else:
    136     # Composite any adjacent images together
    137     image_group = []

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/artist.py:71, in allow_rasterization.<locals>.draw_wrapper(artist, renderer)
     68     if artist.get_agg_filter() is not None:
     69         renderer.start_filter()
---> 71     return draw(artist, renderer)
     72 finally:
     73     if artist.get_agg_filter() is not None:

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/axis.py:1405, in Axis.draw(self, renderer)
   1402 renderer.open_group(__name__, gid=self.get_gid())
   1404 ticks_to_draw = self._update_ticks()
-> 1405 tlb1, tlb2 = self._get_ticklabel_bboxes(ticks_to_draw, renderer)
   1407 for tick in ticks_to_draw:
   1408     tick.draw(renderer)

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/axis.py:1332, in Axis._get_ticklabel_bboxes(self, ticks, renderer)
   1330 if renderer is None:
   1331     renderer = self.get_figure(root=True)._get_renderer()
-> 1332 return ([tick.label1.get_window_extent(renderer)
   1333          for tick in ticks if tick.label1.get_visible()],
   1334         [tick.label2.get_window_extent(renderer)
   1335          for tick in ticks if tick.label2.get_visible()])

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/axis.py:1332, in <listcomp>(.0)
   1330 if renderer is None:
   1331     renderer = self.get_figure(root=True)._get_renderer()
-> 1332 return ([tick.label1.get_window_extent(renderer)
   1333          for tick in ticks if tick.label1.get_visible()],
   1334         [tick.label2.get_window_extent(renderer)
   1335          for tick in ticks if tick.label2.get_visible()])

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/text.py:969, in Text.get_window_extent(self, renderer, dpi)
    964     raise RuntimeError(
    965         "Cannot get window extent of text w/o renderer. You likely "
    966         "want to call 'figure.draw_without_rendering()' first.")
    968 with cbook._setattr_cm(fig, dpi=dpi):
--> 969     bbox, info, descent = self._get_layout(self._renderer)
    970     x, y = self.get_unitless_position()
    971     x, y = self.get_transform().transform((x, y))

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/text.py:373, in Text._get_layout(self, renderer)
    370 ys = []
    372 # Full vertical extent of font, including ascenders and descenders:
--> 373 _, lp_h, lp_d = _get_text_metrics_with_cache(
    374     renderer, "lp", self._fontproperties,
    375     ismath="TeX" if self.get_usetex() else False,
    376     dpi=self.get_figure(root=True).dpi)
    377 min_dy = (lp_h - lp_d) * self._linespacing
    379 for i, line in enumerate(lines):

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/text.py:69, in _get_text_metrics_with_cache(renderer, text, fontprop, ismath, dpi)
     66 """Call ``renderer.get_text_width_height_descent``, caching the results."""
     67 # Cached based on a copy of fontprop so that later in-place mutations of
     68 # the passed-in argument do not mess up the cache.
---> 69 return _get_text_metrics_with_cache_impl(
     70     weakref.ref(renderer), text, fontprop.copy(), ismath, dpi)

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/text.py:77, in _get_text_metrics_with_cache_impl(renderer_ref, text, fontprop, ismath, dpi)
     73 @functools.lru_cache(4096)
     74 def _get_text_metrics_with_cache_impl(
     75         renderer_ref, text, fontprop, ismath, dpi):
     76     # dpi is unused, but participates in cache invalidation (via the renderer).
---> 77     return renderer_ref().get_text_width_height_descent(text, fontprop, ismath)

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/backends/backend_agg.py:211, in RendererAgg.get_text_width_height_descent(self, s, prop, ismath)
    209 _api.check_in_list(["TeX", True, False], ismath=ismath)
    210 if ismath == "TeX":
--> 211     return super().get_text_width_height_descent(s, prop, ismath)
    213 if ismath:
    214     ox, oy, width, height, descent, font_image = \
    215         self.mathtext_parser.parse(s, self.dpi, prop)

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/backend_bases.py:566, in RendererBase.get_text_width_height_descent(self, s, prop, ismath)
    562 fontsize = prop.get_size_in_points()
    564 if ismath == 'TeX':
    565     # todo: handle properties
--> 566     return self.get_texmanager().get_text_width_height_descent(
    567         s, fontsize, renderer=self)
    569 dpi = self.points_to_pixels(72)
    570 if ismath:

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/texmanager.py:364, in TexManager.get_text_width_height_descent(cls, tex, fontsize, renderer)
    362 if tex.strip() == '':
    363     return 0, 0, 0
--> 364 dvifile = cls.make_dvi(tex, fontsize)
    365 dpi_fraction = renderer.points_to_pixels(1.) if renderer else 1
    366 with dviread.Dvi(dvifile, 72 * dpi_fraction) as dvi:

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/texmanager.py:293, in TexManager.make_dvi(cls, tex, fontsize)
    290 with TemporaryDirectory(dir=dvifile.parent) as tmpdir:
    291     Path(tmpdir, "file.tex").write_text(
    292         cls._get_tex_source(tex, fontsize), encoding='utf-8')
--> 293     cls._run_checked_subprocess(
    294         ["latex", "-interaction=nonstopmode", "-halt-on-error",
    295          "-no-shell-escape", "file.tex"], tex, cwd=tmpdir)
    296     Path(tmpdir, "file.dvi").replace(dvifile)
    297     # Also move the tex source to the main cache directory, but
    298     # only for backcompat.

File /opt/hostedtoolcache/Python/3.11.15/x64/lib/python3.11/site-packages/matplotlib/texmanager.py:254, in TexManager._run_checked_subprocess(cls, command, tex, cwd)
    250     report = subprocess.check_output(
    251         command, cwd=cwd if cwd is not None else cls._texcache,
    252         stderr=subprocess.STDOUT)
    253 except FileNotFoundError as exc:
--> 254     raise RuntimeError(
    255         f'Failed to process string with tex because {command[0]} '
    256         'could not be found') from exc
    257 except subprocess.CalledProcessError as exc:
    258     raise RuntimeError(
    259         '{prog} was not able to process the following string:\n'
    260         '{tex!r}\n\n'
   (...)    267             exc=exc.output.decode('utf-8', 'backslashreplace'))
    268         ) from None

RuntimeError: Failed to process string with tex because latex could not be found

<Figure size 640x480 with 1 Axes>

---

Vprašanja za vaje

---

Vprašanje 1: Z uporabo orodij paketa sympy simbolno določite vrednost statičnega momenta prereza v obliki četrtine kroga na sliki:

\[S_{xx} = \int_{A}y~\text{d}A=\int_0^r \int_0^{\pi/2}y(\varphi)~r~\text{d}\varphi~\text{d}r = \int_{0}^{\pi/2}\frac{r^3}{3}\, \sin (\varphi)\, \text{d}\varphi\]

Pripravite tudi numerično funkcijo odvisnosti integranda \(f(\varphi) = \Big(\frac{r^3}{3}\, \sin (\varphi) \Big)\) pri podani vrednosti polmera \(R\).

Podatki:

\(R = 7.5\) mm

Vprašanje 2: Uporabite numerično funkcijo, pripravljeno pri prejšnji nalogi, in izračunajte ter grafično prikažite vrednosti integranda iz prve naloge \(\Big(f(\varphi) = \frac{r^3}{3}\sin (\varphi) \Big)\) pri 100 diskretnih točkah na intervalu \(\varphi \in [0, \pi/2]\).

Izračunajte vrednost določenega integrala \(S\) še numerično, s pomočjo trapezne in Simpsonove 1/3 metode iz paketov numpy oziroma scipy.

\[ S = \int_{0}^{\pi/2}\frac{r^3}{3}\sin (\varphi)\text{d}\varphi\]

---

Trapezno pravilo

Vprašanje 3: Z uporabo lastne implementacije trapeznega pravila (osnovnega, ne sestavljenega) izračunajte določeni integral

\[I = \int_{0}^{2} -0.5x^3 - x^2 + 8 ~\text{d}x\]

Dobljeno vrednost primerjajte z rezultatom funkcije numpy.trapz (ali scipy.integrate.trapezoid), kjer opazovan interval razdelite na 10 ekvidistantnih odsekov.

---

Izboljšan približek z Richardsonovo esktrapolacijo:

\[\bar{I} = \frac{4I_h - I_{2h}}{3}\]

Vprašanje 4 : Uporabite Richardsonovo ekstrapolacijo in določite natančnejšo vrednost integrala iz prejšnje naloge tako, da opazovan interval \(x \in [0, 2]\) najprej razdelite na 2, nato še na 4 ekvidistantne segmente in uporabite sestavljeno trapezno metodo iz paketa numpy.

---

Simpsonovo 1/3 pravilo

Vprašanje 5: Določen integral iz prejšnje naloge izračunajte z lastno kodo Simpsonove 1/3 metode (osnovne, ne sestavljene).

\[I = \int_{0}^{2} -0.5x^3 - x^2 + 8 ~\text{d}x\]

Dobljeno vrednost primerjajte z rezultatom funkcije scipy.integrate.simpson, kjer opazovan interval razdelite na 7 ekvidistantnih točk.

---

Vprašanje 6: Podane so izmerjene vrednosti pospeška avtomobila v smeri vožnje v času. Z uporabo kumulativne trapezne metode (scipy.integrate.cumulative_trapezoid) določite vrednosti hitrosti in opravljene poti avtomobila v opazovanm časovnem intervalu.

Avto pri času \(t = 0\) miruje (namig: argument initial).

#Podatki
t = np.linspace(0, 7, 10) # s
a = np.array([ 3.47,  4.03,  4.36,  4.48,  4.27,  3.78,  3.19,  2.73,  2.54,  2.53]) # m/s^2

---

Gaussova integracijska metoda (Gaussova kvadratura)

Vprašanje 7: Z uporabo sestavljene trapezne metode iz scipy in metode Gaussove integracije (scipy.integrate.quad) izračunajte vrednosti integralov:

\[I_1 = \int_{0}^{1}\frac{\sin(x)}{x} \text{d}x\]

\[I_2 = \int_{1}^{2}\frac{\sin(x)}{x} \text{d}x\]

\[I_3 = \int_{-0.5}^{0.5}\frac{\sin(x)}{x} \text{d}x\]

Pri uporabi trapezne metode razdelite opazovan interval na 10 točk.

Vprašanje 8: Integral:

\[I = \int_{-0.5}^{0.5}\frac{\sin(x)}{x} \text{d}x\]

izračunajte še z uporabo funkcije scipy.integrate.fixed_quad, ki ji lahko podamo tudi parameter števila vozlišč pri integraciji, n. Najprej uporabite integracijo z enim vozliščem, nato z dvema in nazadnje še s tremi vozlišči.