Objektno programiranje, simbolno računanje#
Objektno programiranje#
Pri programiranju poznamo različne pristope, dokumentacija Python-a (docs.python.org) omenja npr:
proceduralni: seznam navodil, kaj je treba izvesti (npr.:
C, Pascal)deklerativni: opišemo kaj želimo, programski jezik pa izvede (npr.,
SQL)funkcijski: programiranje temelji na funkcijah (npr.:
Haskell)objektni: program temelji na objektih, ki imajo lastnosti, funkcije … (npr.:
Java, Smalltalk)
Python je objektno orientiran programski jezik, vendar pa nas ne sili v uporabo objektov v vseh primerih. Kot bomo videli pozneje, ima objektno programiranje veliko prednosti, vendar pa je lahko mnogokrat okorno in bi po nepotrebnem naredilo program kompleksen. Iz tega razloga se eksplicitnemu objektnemu programiranju izognemo, če se le da.
Objektno programiranje v Pythonu temelji na razredih (class), objekti so pa instance (instance) razreda. Pogledali si bomo zgolj nekatere osnove objektnega programiranja (da boste lažje razumeli kodo drugih avtorjev in jo prirejali svojim potrebam).
Razred definiramo z ukazom class (dokumentacija):
class ImeRazreda:
'''docstring'''
[izraz 1]
[izraz 2]
.
.
kjer ime razreda (torej ImeRazreda) po PEP8 pišemo z veliko začetnico. Če je ime sestavljeno iz več besed, vsako pišemo z veliko (t. i. principi CamelCase).
Poglejmo si primer:
class Pravokotnik:
"""Razred za objekt pravokotnik"""
def __init__(self, širina=1, višina=1): # to je konstruktor objekta. Se izvede, ko kličemo Pravokotnik(sirina=1, visina=4)
self.širina = širina
self.višina = višina # višina je atribut objekta
def površina(self):
return self.širina * self.višina
def set_širina(self, širina=1):
self.širina = širina
Preden gremo v podrobnosti razumevanja kode, naredimo instanco razreda (torej objekt):
moj_pravokotnik = Pravokotnik()
Funkcije definirane znotraj razreda poimenujemo metode, ko jih kličemo na objektih.
V zgornjem primeru metodo površina uporabimo tako:
moj_pravokotnik.površina()
1
Ime self je referenca na instanco razreda (objekt, ki bo ustvarjen). Imena znotraj razreda postanejo atributi objekta.
Primer atributa `višina˙:
moj_pravokotnik.višina
1
Od kje pride rezultat 1? Ko ustvarimo objekt, se najprej izvede inicializacijska funkcija __init__(), pri tem se kot argumenti funkcije __init__ uporabijo argumenti, ki jih posredujemo v razred.
Primer:
tvoj_pravokotnik = Pravokotnik(višina=5, širina=3)
tvoj_pravokotnik.površina()
15
Pripravili smo tudi metodo, ki spremeni atribut širina:
moj_pravokotnik.set_širina(širina=100)
moj_pravokotnik.površina()
100
Atribute lahko spreminjamo tudi neposredno, vendar se temu (zaradi možnosti napake in napačne uporabe) ponavadi izogibamo.
Primer:
moj_pravokotnik.višina = 3
moj_pravokotnik.površina()
300
Dedovanje#
Pomembna lastnost razredov je dedovanje; samo ime pove bistvo: tako kot ljudje dedujemo od svojih staršev, podobno velja tudi za razrede. Vsak razred (class) tako lahko deduje lastnosti kakega drugega razreda (dokumentacija). Lahko ima celo več staršev (v te podrobnosti tukaj ne bomo šli).
Sintaksa razreda, ki deduje, je:
class Otrok(Starš):
[izraz]
.
.
Opomba: tudi, če razredu ne definiramo starša, deduje razred class.
Primer, ko novi razred Kvadrat podeduje obstoječega (Pravokotnik):
class Kvadrat(Pravokotnik):
"Razred kvadrat"
def __init__(self, širina=1):
# kličimo iniciacijo razreda Pravokotnik
super().__init__(širina=širina, višina=širina)
def set_širina(self, širina):
self.širina = širina
self.višina = širina
Poglejmo sedaj uporabo:
moj_kvadrat = Kvadrat(širina=4)
Razred Kvadrat nima definicije metode za izračun površine, vendar pa jo je podedoval od razreda Pravokotnik in zato ima metodo za izračun površine:
moj_kvadrat.površina()
16
V kolikor spremenimo širino, se ustrezno spremeni površina:
moj_kvadrat.set_širina(5)
moj_kvadrat.površina()
25
Primer dedovanja razreda list (seznam)#
Najprej pripravimo seznam:
seznam = list([1,2,3])
seznam
[1, 2, 3]
Če želimo seznamu dodati vrednost, uporabimo metodo append (to je metoda, ki jo imajo objekti tipa list):
seznam.append(1)
Nato seznam prikažemo (najprej uvozimo matplotlib):
import matplotlib.pyplot as plt
plt.plot(seznam)
plt.show()
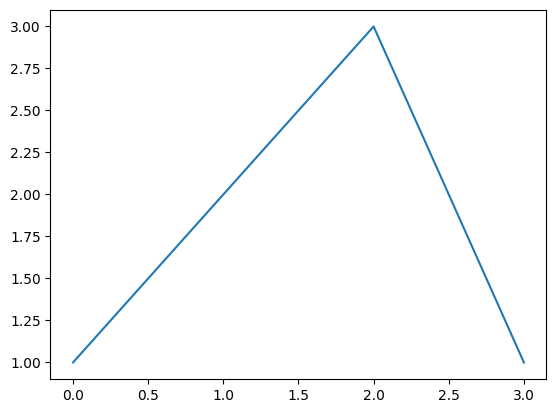
Če nekaj takega izvajamo pogosto, potem je bolje, da si pripravimo svoj razred Seznam, ki deduje od list in dodamo metodo za prikaz nariši:
class Seznam(list):
def nariši(self):
plt.plot(self, 'r.', label='Dolgo besedilo')
plt.legend()
plt.ylim(-5, 5)
plt.show()
Instanca objekta je:
moj_seznam = Seznam([1, 2, 3])
type(moj_seznam)
__main__.Seznam
moj_seznam
[1, 2, 3]
Čeprav nismo definirali metode append, jo je nov razred podedoval po razredu list:
moj_seznam.append(1)
moj_seznam
[1, 2, 3, 1]
Ima tudi metodo za izris:
moj_seznam.nariši()
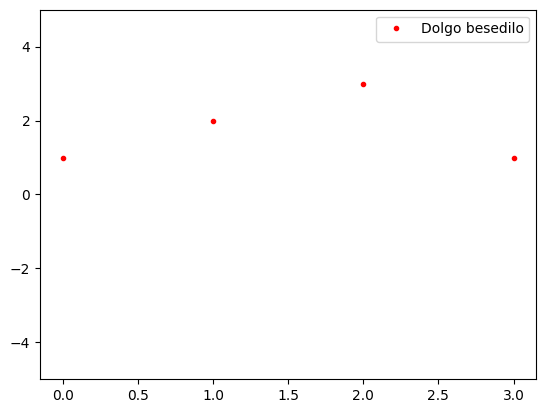
Simbolno računanje s SymPy#
Termin simbolno računanje pomeni, da matematične izraze rešujemo strojno v obliki abstraktnih simbolov (in ne numerično). Strojno simbolno računanje nam pomaga kadar nas zanima rezultat v simbolni obliki in so izrazi preobsežni za klasično reševanje na list in papir. K strojnemu reševanju se zatečemo tudi zaradi zmanjšanja možnosti napake (pri obsežnih izračunih se ljudje lahko zmotimo).
Simbolno računanje nikakor ni nadomestek numeričnih metod!
Pogledali si bomo nekatere osnove, nekateri priporočeni dodatni viri pa so:
J.R. Johansson Scientific python lectures,
SymPy - uradna dokumentacija modula,
Odličen članek nekaterih avtorjev SymPy: Meurer et. al, 2017.
SymPy je eden od sistemov za strojno algebro (CAS - Computer Algebra Systems), ki pa ima poleg zmogljivosti tudi to prednost, da je v celoti napisan v Pythonu (alternativni paket v Pythonu Sage na primer ni v celoti napisan v Pythonu).
Nekatera namenska komercialna orodja:
Najprej uvozimo modul SymPy; tipično paket uvozimo kot sym:
import sympy as sym
Opazimo lahko, da se SymPy uvaža tudi from sympy import *. Temu se praviloma izogibamo, saj tako s SymPy imeni po nepotrebnem zapolnimo osnovni imenski prostor programa. V slednjem primeru do funkcij paketa (npr. sympy.Sum) dostopamo neposredno (npr. Sum), kar je lahko privlačno, vendar nas začne motiti, ko dodamo še druge pakete (npr. numpy), kar lahko poleg zmede privede do tega, da se funkcije z enakimi imeni „povozijo“.
Zato da dobimo lepo oblikovan LaTeX izpis, uporabimo:
sym.init_printing()
Definiranje spremenljivk in numerični izračun#
Spremenljivke definiramo takole:
x, y, k = sym.symbols('x, y, k')
Preverimo lahko tip:
type(x)
sympy.core.symbol.Symbol
Opazimo, da je spremenljivka x sedaj Symbol iz paketa sympy.
Sedaj lahko naredimo preprost izračun:
x**y + k

Funkcijo lahko tudi poimenujemo; tukaj je primer, kjer uporabimo funkcijo sinus in konstanto \(\pi\):
f = sym.sin(1.2*sym.pi + x)**2
f
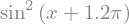
Bralec se morebiti sprašuje, zakaj potrebujemo novo funkcijo sympy.sin(), saj imamo vendar že tisto iz paketa numpy! Razlog je v tem, da simbolni izračun potrebuje popolnoma drugačno obravnavo kakor numerični in zato je koda zadaj povsem drugačna.
Če želimo zapisati enačbo, torej da enačimo en izraz z drugim, to naredimo takole:
enačba = sym.Eq(sym.sin(k*x),0.5)
enačba

Nedefinirane matematične funkcije zapišemo kot (dokumentacija):
g = sym.Function('g')
Sedaj lahko, na primer, definiramo differencialno enačbo:
sym.Eq(g(x).diff(x), x)
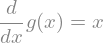
Pri definiranju spremenljivk lahko dodajamo predpostavke:
x = sym.Symbol('x', positive=True)
x.is_positive
True
Predpostavke se potem upoštevajo pri izračunu. V splošnem vemo, da \(\sqrt{(x^2)}\ne x\), če pa je \(x\) pozitiven, pa velja \(\sqrt{(x^2)}= x\) in sympy glede na predpostavke izračuna pravilen rezultat:
sym.sqrt(x**2)
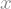
Z metodo assumptions0 pogledamo predpostavke objekta:
x.assumptions0
{'commutative': True,
'complex': True,
'extended_negative': False,
'extended_nonnegative': True,
'extended_nonpositive': False,
'extended_nonzero': True,
'extended_positive': True,
'extended_real': True,
'finite': True,
'hermitian': True,
'imaginary': False,
'infinite': False,
'negative': False,
'nonnegative': True,
'nonpositive': False,
'nonzero': True,
'positive': True,
'real': True,
'zero': False}
SymPy pozna tipe števil (dokumentacija):
Realrealna števila,Rationalracionalna števila,Complexkompleksna števila,Integercela števila.
Ti tipi so pomembni, saj lahko vplivajo na način reševanja in na rešitev.
Racionalna števila#
Zgoraj smo že definirali realna števila. Poglejmo na primeru sedaj racionalna števila:
r1 = sym.Rational(4, 5)
r2 = sym.Rational(5, 4)
r1

Nekateri izračuni:
r1+r2

r1/r2

Kompleksna števila#
Imaginarno število se zapiše z I (to je drugače kot pri numpy, kjer je imaginarni del definiran z j):
1+1*sym.I

sym.I**2

Numerični izračun#
Pri simbolnem izračunu najprej analitične izraze rešimo, poenostavimo itd., nato pa pogosto želimo tudi izračunati konkreten rezultat.
Poglejmo primer:
x = sym.symbols('x')
f = sym.exp(x**x**x + sym.pi)
f
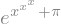
Če želimo sedaj namesto \(x\) uporabiti vrednost, npr 0.5, to naredimo z metodo subs() (dokumentacija):
f.subs(x, 0.5)
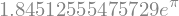
Zgoraj smo uporabili konstanto \(\pi\) (dokumentacija); nekatere tipično uporabljene konstante so:
sympy.piza število \(\pi\),sympy.Eza naravno število \(e\),sympy.ooza neskončnost.
Kot smo videli zgoraj, subs() naredi zamenjavo in potem poenostavitve, ki so očitne; števila \(\pi\) ni izračunal v racionalni obliki. To moramo eksplicitno zahtevati z metodo:
evalf(angl. *evaluate function, dokumentacija) aliN,
kateri imata obe argument n (število števk).
Poglejmo primer:
f.subs(x, 2).evalf(n=80)
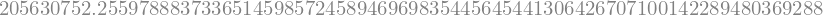
Podobno je z N:
sym.N(f.subs(x, 2), n=80)
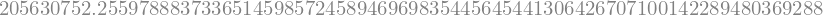
Mimogrede smo pokazali, da pod pogojem, da v izrazu nimamo števil s plavajočo vejico, lahko rezultat prikažemo poljubno natančno (dokumentacija).
V subs funkciji lahko uporabimo tudi slovar. Primer:
x, y = sym.symbols('x, y')
parametri = {x: 4, y: 10}
(x + y).subs(parametri)

ali seznam terk:
(x + y).subs([(x, 4), (y, 10)])

Podobno ima metoda sympy.evalf() argument subs, ki sprejme slovar zamenjav, primer:
(y**x).evalf(subs=parametri)
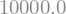
Metoda sympy.subs pa lahko zamenja simbol (ali izraz) tudi z drugim izrazom:
(x + y).subs(x, y + sym.oo)

SymPy in NumPy#
Pogosto sympy povežemo z numpy. Za primer si poglejmo, kako bi izraz:
x = sym.symbols('x')
f = sym.sin(x) + sym.exp(x)
f

numerično učinkovito izračunali pri tisoč vrednostih \(x\).
Najprej uvozimo paket numpy:
import numpy as np
Pripravimo numerično polje vrednosti:
x_vec = np.linspace(0, 10, 1000, endpoint=False)
x_vec[:10]
array([0. , 0.01, 0.02, 0.03, 0.04, 0.05, 0.06, 0.07, 0.08, 0.09])
Glede na zapisano zgoraj in predhodno znanje uporabimo izpeljevanje seznamov:
y_vec = np.array([f.evalf(subs={x: vrednost}) for vrednost in x_vec])
Opazimo, da je to dolgotrajno, zato izmerimo potreben čas:
%%timeit -n1
y_vec = np.array([f.evalf(subs={x: vrednost}) for vrednost in x_vec])
62.9 ms ± 3.98 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
Uporaba funkcije lambdify#
Bistveno hitrejši način je uporaba pristopa lambdify, kjer se pripravi prevedena funkcija, optimirana za numerično izvajanje. Sintaksa funkcije sympy.lambdify() je (dokumentacija):
sympy.lambdify(simboli, funkcija, modules=None)
kjer so argumenti:
simbolisimboli uporabljeni vfunkcija, ki se zamenjajo z numeričnimi vrednostmi,funkcijapredstavljasympyfunkcijo,modulespredstavlja, za kateri paket je prevedena oblika pripravljena. Če jenumpynameščen, je privzeto za ta modul.
Primer uporabe:
f_hitra = sym.lambdify(x, f, modules='numpy')
y_vec_hitra = f_hitra(x_vec)
Preverimo hitrost:
%%timeit -n100
f_hitra(x_vec)
13.4 μs ± 2.69 μs per loop (mean ± std. dev. of 7 runs, 100 loops each)
Opazimo približno 10.000-kratno pohitritev!
Poglejmo še primer uporabe funkcije več spremenljivk:
f_hitra2 = sym.lambdify((x, y), (x + y + sym.pi)**2, 'numpy')
x = np.linspace(0, 10, 10)
y = x
f_hitra2(x, y)
array([ 9.8696044 , 28.77051002, 57.54795885, 96.20195089,
144.73248614, 203.1395646 , 271.42318627, 349.58335115,
437.62005924, 535.53331054])
Grafični prikaz#
SymPy ima na matplotlib temelječ prikaz podatkov. Prikaz je sicer glede na matplotlib bolj omejen in ga uporabljamo za preproste prikaze. (dokumentacija).
Pogledali si bomo preproste primere, ki se navezujejo na funkcijo sympy.plotting.plot; najprej uvozimo funkcijo:
from sympy.plotting import plot
Sintaksa uporabe funkcije sympy.plotting.plot() (dokumentacija) je:
plot(izraz, razpon, **kwargs)
kjer so argumenti:
izrazje matematični izraz ali več izrazov,razponje razpon prikaza (privzeti razpon je (-10, 10)),**kwargsso keyword arguments, torej slovar različnih možnosti.
Funkcija vrne instanco objekta sympy.Plot().
Minimalni primer ene funkcije:
x = sym.symbols('x')
plot(x**2)
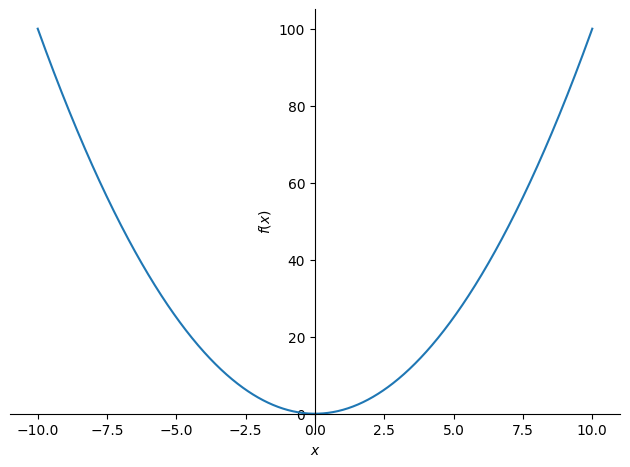
<sympy.plotting.backends.matplotlibbackend.matplotlib.MatplotlibBackend at 0x2620cf3fe60>
Opomba: zadnja vrstica opozori na rezultat v obliki instance Plot; izpis objekta <sympy.plotting.plot.Plot at 0x...> skrijemo z uporabo podpičja:
plot(x**2);
slika pa se vseeno prikaže.
Nekateri pogosti argumenti so:
showprikaže sliko (privzetoTrue),line_colorbarva izrisa,xscaleinyscalenačin prikaza (možnosti:linearalilog),xliminylimomejitev prikaza za osi (terka dveh(min, max)vrednosti).
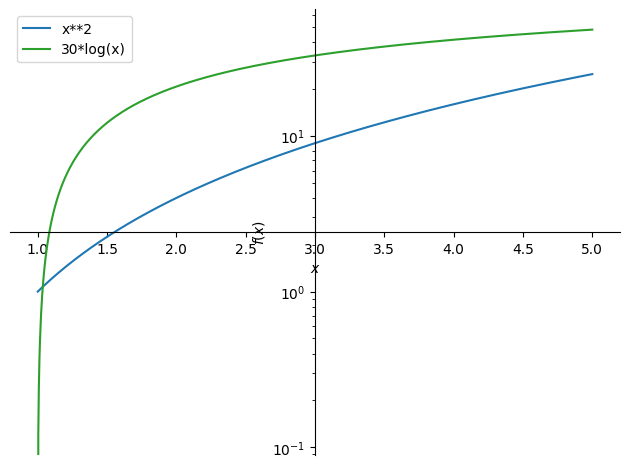
Pripravimo dve sliki, kjer bo \(y\) os logaritemska in bo razpon izrisa od 1 do 5:
izris1 = plot(x**2, (x, 1, 5), show=False, legend=True, yscale='log')
izris2 = plot(30*sym.log(x), (x, 1, 5), show=False, line_color='C2', legend=True, yscale='log')
Sedaj prvo sliko razširimo z drugo in prikažemo rezultat:
izris1.extend(izris2)
izris1.show()
Parametrični izris#
Podobno uporabljamo funkcijo sympy.plotting.plot_parametric za parametrični izris (dokumentacija):
plot_parametric(izraz_x, izraz_y, range, **kwargs)
kjer sta nova argumenta:
izraz_xinizraz_ydefinicije lege koordinate \(x\) in \(y\),**kwargsje slovar možnosti.
Uvozimo funkcijo:
from sympy.plotting import plot_parametric
Prikažimo uporabo na primeru:
plot_parametric(sym.sin(x), sym.sin(2*x), (x, 0, 2*sym.pi));
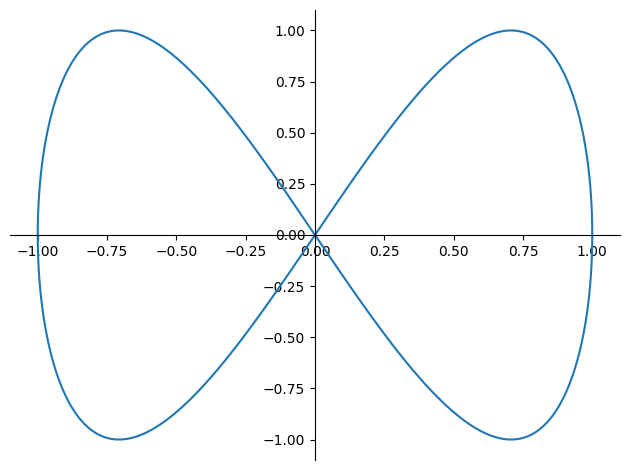
Izris v prostoru#
Funkcija sympy.plotting.plot3D (dokumentacija) za izris v prostoru ima sintakso:
plot3d(izraz, razpon_x, razpon_y, **kwargs)
kjer so argumenti:
izrazdefinicija površine,razpon_xinrazpon_yrazpon koordinatexiny,**kwargsslovar možnosti.
Uvozimo funkcijo:
from sympy.plotting import plot3d
Prikažimo uporabo na primeru:
x, y = sym.symbols('x y')
plot3d(x**2 + y**2, (x, -5, 5), (y, -5, 5));
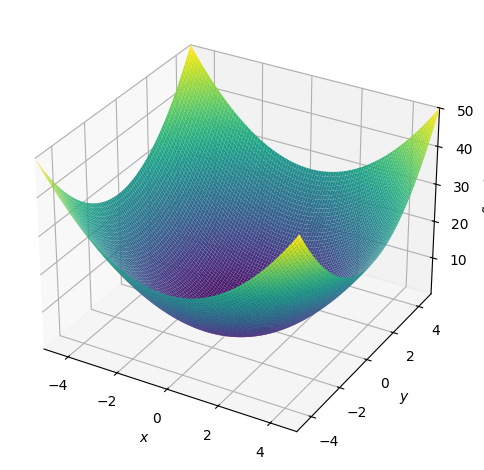
Za ostale prikaze glejte dokumentacijo.
Algebra#
V tem poglavju si bomo pogledali nekatere osnove uporabe SymPy za algebrajske operacije.
Uporaba expand in factor#
Definirajmo matematični izraz:
x = sym.symbols('x')
f = (x+1)*(x+2)*(x+3)
f

in ga sedaj razčlenimo (angl. expand, glejte dokumentacijo):
aa = sym.expand(f)
aa

Če želimo pogledati koeficiente pred x, to naredimo z metodo coeff():
aa.coeff(x)

Argumenti funkcije definirajo, kakšno razširitev želimo (dokumentacija). Če želimo npr. trigonometrično razširitev, potem uporabimo trig=True:
a, b = sym.symbols('a, b')
sym.expand(sym.sin(a+b))

sym.expand(sym.sin(a+b), trig=True)

Obratna operacija od razčlenitve je razcepitev ali razstavljanje ali faktorizacija (angl. factor, dokumentacija):
sym.factor(x**3 + 6 * x**2 + 11*x + 6)

Če nas zanimajo posamezni členi, potem to naredimo s funkcijo sympy.factor_list:
sym.factor_list(x**3 + 6 * x**2 + 11*x + 6)

Poenostavljanje izrazov s simplify#
Funkcija sympy.simplify() (dokumentacija) poskuša poenostaviti izraze v bolj preproste (npr. s krajšanjem spremenljivk).
Za posebne namene lahko poenostavimo tudi z:
Za več glejte dokumentacijo.
Primeri poenostavljanja:
sym.simplify((x+1)*(x+1)*(x+3))
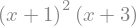
sym.simplify(sym.sin(a)**2 + sym.cos(a)**2)

sym.simplify(sym.cos(x)/sym.sin(x))
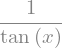
Uporaba apart in together#
Funkciji uporabljamo za delo z ulomki:
f1 = 1/((1 + x) * (5 + x))
f1
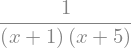
Razcep na parcialne ulomke (angl. partial fraction decomposition) izvedemo s funkcijo sympy.apart() (dokumentacija):
f2 = sym.apart(f1, x)
f2
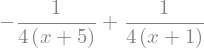
in potem ponovno v obratni smeri s funkcijo sympy.together():
sym.together(f2)
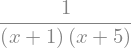
V slednjem primeru pridemo do podobnega rezultata s sympy.simplify():
sym.simplify(f2)
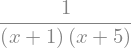
Odvajanje#
Odvajanje je načeloma relativno preprosta matematična operacija, ki jo izvedemo s funkcijo sympy.diff() (dokumentacija):
Pripravimo primer:
x, y, z = sym.symbols('x, y, z')
f = sym.sin(x*y) + sym.cos(y*z)
f

Odvajajmo ga po \(x\):
sym.diff(f, x)
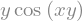
ali tudi
f.diff(x)
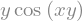
Odvode višjega reda definiramo tako:
sym.diff(f, x, x, x)

ali (isti rezultat malo drugače):
sym.diff(f, x, 3)

Odvod po več spremenljivkah \(\frac{d^3f}{dx\,dy^2}\) izvedemo takole:
sym.diff(f, x, 1, y, 2)
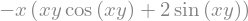
Integriranje#
Funkcijo integrate lahko uporabimo za nedoločeno integriranje (dokumentacija):
integrate(f, x)
ali za določeno integriranje:
integrate(f, (x, a, b))
kjer so argumenti:
ffunkcija, ki jo integriramo,xspremenljivka, po kateri integriramo,ainbmeje integriranja.
Primer nedoločenega integriranja:
x = sym.symbols('x')
f = sym.sin(x*y) + sym.cos(y*z)
sym.integrate(f, x)
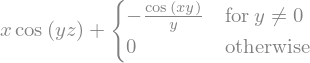
Opazimo, da sympy pravilno upošteva možnost, da je \(y=0\).
Še primer določenega integriranja:
sym.integrate(f, (x, -1, 1))
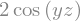
Primer, ko so meje v neskončnosti (uporabimo konstanto za neskončnost sympy.oo):
sym.integrate(sym.exp(-x**2), (x, -sym.oo, sym.oo))

Vsota in produkt vrste#
Vsoto vrste definiramo s pomočju funkcije sympy.Sum() (dokumentacija):
sympy.Sum(izraz, (spr, start, end))
kjer so argumenti:
izrazizraz, katerega seštevamo,spr,startinendspremenljivka, ki naračša odstartdoend(endje vključen).
Primer vsote vrste:
n = sym.Symbol('n')
f = sym.Sum(1/x**n, (n, 1, sym.oo))
f
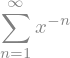
Šele ko uporabimo metodo doit_(), se izračun izvede:
f.doit()
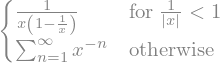
Poglejmo še številčni rezultat:
f.subs({x: 5}).evalf()
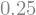
Produkt vrste definiramo podobno s funkcijo sympy.Product (dokumentacija):
sympy.Product(izraz, (spr, start, end))
kjer so argumenti:
izrazizraz, katerega množimo,spr,startinendspremenljivka, ki naračša odstartdoend(endje vključen).
Primer:
f = sym.Product(1/n, (n, 1, 5))
f
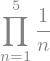
f.doit()
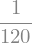
Limitni račun#
Limite računamo s pomočjo funkcije sympy.limit() (dokumentacija):
sympy.limit(f, x, x0)
kjer so argumenti:
fizraz, katerega limito iščemo,xspremenljivka, ki limitira protix0,x0limita.
Primer:
x = sym.symbols('x')
f = sym.sin(x)/x
f
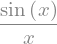
sym.limit(f, x, 0)

Za primer si poglejmo uporabo limite na definiciji odvoda:
Pripravimo funkcijo f in njen odvod:
x, y, z, h = sym.symbols('x, y, z, h')
f = sym.sin(x*y) + sym.cos(y*z)
Odvod funkcije je:
sym.diff(f, x)
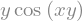
Enak rezultat izračunamo tudi z uporabo limite:
sym.limit((f.subs(x, x+h) - f)/h, h, 0)
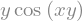
Taylorjeve vrste#
Taylorjeve vrste izračunamo s pomočjo funkcijo sympy.series() (dokumentacija):
sympy.series(izraz, x=None, x0=0, n=6, dir='+')
kjer so argumenti:
izrazizraz, katerega vrsto določamo,xneodvisna spremenljivka,x0vrednost, okoli katere določamo vrsto (privzeto 0),nred vrste (privzeto 6),dirsmer razvoja vrste (+ali-).
Primer:
x = sym.symbols('x')
sym.series(sym.exp(x), x) # privzete vrednosti x0=0, in n=6
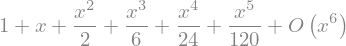
Če želimo definirati drugo izhodišče (x0=2) in z več členi (n=8), to izvedemo takole:
s1 = sym.series(sym.exp(x), x, x0=2, n=8)
s1
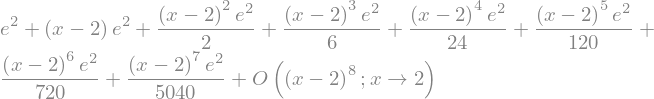
Rezultat vključuje tudi red veljavnosti; na ta način lahko kontroliramo veljavnosti izvajanja (\(\mathcal{O}\)).
Primer:
s1 = sym.cos(x).series(x, 0, 5)
s1
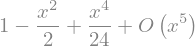
s2 = sym.sin(x).series(x, 0, 2)
s2

Izračuna s1 in s2 imata različna reda veljavnosti, posledično je produkt:
s1 * s2
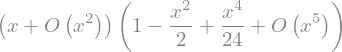
natančen samo do reda \(\mathcal{O}(x^2)\), kar sympy ustrezno obravnava:
s3 = sym.simplify(s1 * s2)
s3

Podatek o stopnji veljavnosti lahko odstranimo:
s3.removeO()
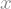
Linearna algebra#
Matrike in vektorji#
Matrike in vektorje definiramo s funkcjo Matrix. Če se pri numpy.array ni treba dosledno držati matematičnega zapisa vektorjev in matrik, je pri sympy to nujno.
Poglejmo si primer; najprej pripravimo spremenljivke:
m11, m12, m21, m22 = sym.symbols('m11, m12, m21, m22')
b1, b2 = sym.symbols('b1, b2')
Nato matriko in stolpični vektor:
A = sym.Matrix([[m11, m12],[m21, m22]])
A
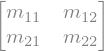
b = sym.Matrix([[b1], [b2]])
b
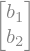
Sedaj si poglejmo nekatere tipične operacije; najprej množenje matrike in vektorja:
A * b
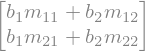
Nato skalarni produkt dveh vektorjev (paziti moramo na transponiranje enega od vektorjev):
b.T*b

Determinanta in inverzna matrika:
A.det()

A.inv()
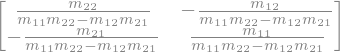
Množenje in potenca matrike:
A*A
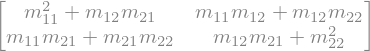
A**2
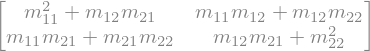
Reševanje enačb#
Enačbe in sistem enačb rešujemo s funkcijo sympy.solve() (dokumentacija). Podprto je reševanje sledečih enačb:
polinomske enačbe,
transcendentne enačbe,
odsekovno definirane enačbe kot kombinacija zgornjih dveh tipov,
sistem linearnih in polinomskih enačb,
sistem enačb z neenakostmi.
Sintaksa je:
sympy.solve(f, *symbols, **flags)
kjer so argumenti:
fizraz ali seznam izrazov,*symbolssimbol ali seznam simbolov, katere želimo določiti,**flagsslovar možnosti.
Poglejmo primer:
x = sym.symbols('x')
f = sym.sin(x)
en = sym.Eq(f, 1/2)
en
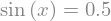
sym.solve(en, x)
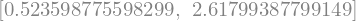
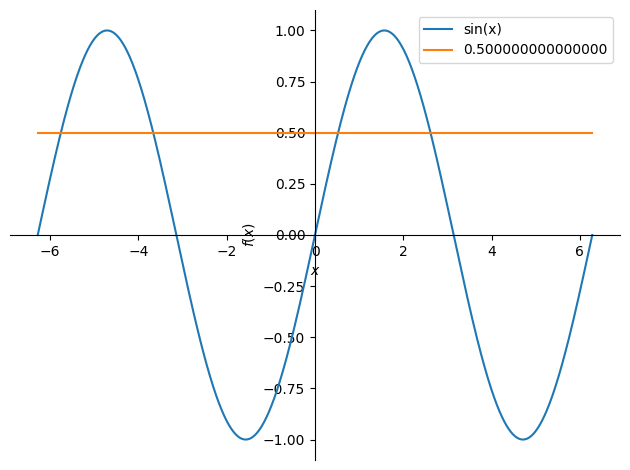
Prikažimo rešitev (opazimo, da smo našli samo dve od neskončno rešitev):
p1 = sym.plotting.plot(sym.sin(x), (x, -2*sym.pi, 2*sym.pi), line_color='C0', show=False, legend=True)
p2 = sym.plotting.plot(0.5, (x, -2*sym.pi, 2*sym.pi), line_color='C1', show=False, legend=True)
p1.extend(p2)
p1.show()
Kvadratna enačba:
a, b, c, x = sym.symbols('a, b, c, x')
sym.solve(a*x**2 + b*x + c, x)
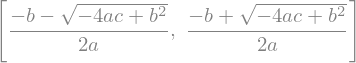
Sistem enačb:
x, y = sym.symbols('x y')
sym.solve([x + y - 1, x - y - 1], [x, y])

Za nelinearne sisteme pa lahko uporabimo tudi numerično reševanje s funkcijo sympy.nsolve() (dokumentacija):
sympy.nsolve(f, [args,] x0, modules=['mpmath'], **kwargs)
kjer so argumenti:
fenačba ali sistem enačb, ki ga rešujemo,argsspremenljivke (opcijsko),x0začetni približek (skalar ali vektor),modulespaket, ki se uporabi za izračun numerične vrednosti (enaka logika kot pri funkcijilambdify, privzet je paketmpmath),**kwargsslovar opcij.
Poglejmo primer od zgoraj:
x = sym.symbols('x')
eq = sym.Eq(sym.sin(x), 0.5)
sol = sym.nsolve(en, x, 3)
sol
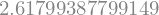
Reševanje diferencialnih enačb#
Nedefinirane funkcije#
Preden si ogledamo diferencialne enačbe, moramo spoznati nedefinirane funkcije. Take funkcije definiramo sympy.Function dokumentacija.
Kot primer si poglejmo kako definiramo enačbo \(\ddot x(t)=g\). Najprej definirajmo nedoločeno funkcijo:
x = sym.Function('x')
Nato simbole:
t, g = sym.symbols('t, g')
In še enačbo:
sym.Eq(x(t).diff(t,2), g)
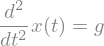
Diferencialne enačbe#
Diferencialne enačbe in sisteme diferencialnih enačb rešujemo s funkcijo sympy.dsolve() (dokumentacija):
sympy.dsolve(eq, func=None, hint='default', simplify=True,
ics=None, xi=None, eta=None, x0=0, n=6, **kwargs)
kjer so izbrani argumenti:
eqdifferencialna enačba ali sistem diferencialnih enačb,funcrešitev, ki jo iščemo,icszačetni in robni pogoji diferencialne enačbe.
Poglejmo si primer mase \(m\), ki drsi po površini s koeficientom trenja \(\mu\); začetna hitrost je \(v_0\), pomik \(x_0=0\).
Definirajmo simbole:
x = sym.Function('x')
t, m, mu, g, v0, x0 = sym.symbols('t m mu g v0 x0', real=True, positive=True)
Definirajmo diferencialno enačbo:
eq = sym.Eq(m*x(t).diff(t,2), -mu*g*m)
eq
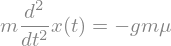
Poglejmo lastnosti diferencialne enačbe:
sym.ode_order(eq, x(t))
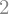
sym.classify_ode(eq)
('factorable',
'nth_algebraic',
'nth_linear_constant_coeff_undetermined_coefficients',
'nth_linear_euler_eq_nonhomogeneous_undetermined_coefficients',
'nth_linear_constant_coeff_variation_of_parameters',
'nth_linear_euler_eq_nonhomogeneous_variation_of_parameters',
'nth_algebraic_Integral',
'nth_linear_constant_coeff_variation_of_parameters_Integral',
'nth_linear_euler_eq_nonhomogeneous_variation_of_parameters_Integral',
'2nd_nonlinear_autonomous_conserved',
'2nd_nonlinear_autonomous_conserved_Integral')
Rešimo jo:
rešitev = sym.dsolve(eq, x(t),
ics={
x(0):0, #pri času 0s je pomik nič
x(t).diff(t).subs(t, 0): v0 #pri času 0s je hitrost enaka v0
})
rešitev
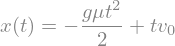
Desno stran enačbe prikličemo takole (rhs - right-hand side):
rešitev.rhs
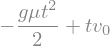
Dodatno#
sympy.mechanics#
sympy ima vgrajeno podporo za klasično mehaniko (dokumentacija). Celovit tutorial je bil prikazan na znanstveni konferenci SciPy 2016.
Vprašanja za vaje#
Osnove objektnega programiranja#
Vprašanje 1: Pripravite razred KompleksnoStevilo, ki v konstruktorju dva podana argumenta shrani v atributa self.re in self.im. Ustvarite objekt pripravljenega razreda, izpišite re in im.
Vprašanje 2: Razred KompleksnoStevilo nadgradite z metodo konjugiran(), ki bo omogočalo kompleksno konjugacijo objektov.
Vprašanje 3: Razred iz prejšnje naloge nadgradite z metodo absolutno(), ki izračuna in vrne absolutno vrednost kompleksnega števila, \(|a + \text{i}\,b| = \sqrt{a^2 + b^2}\).
Vprašanje 4: Pripravite razred RealnoStevilo, ki deduje za razredom KompleksnoStevilo. V funkciji __init__ naj pokliče konstruktor glavnega razreda, realnemu delu priredi podano vrednost, imaginarnemu pa vedno vrednost 0.
SymPy#
Vprašanje 5: Z uporabo paketa SymPy definirajte potrebne simbole in definirajte izraze za kinetično in potencialno energijo \(E_k\), \(E_p\) ter Lagrangevo energijsko funkcijo \(L\) sistema mase in vzmeti . Vse simbole definirajte kot pozitivna realna števila.
Vprašanje 6: Z uporabo spodaj zapisane enačbe nastavite gibalno enačbo sistema mase in vzmeti.
Vprašanje 7: Z uporabo SymPy funkcije rešite dobljeno diferencialno enačbo. Definirajte nov simbol w in v dobljeni rešitvi opravite zamenjavo: \(\sqrt{\frac{k}{m}} = \omega\). Desno stran enačbe shranite v spremenljivko pomik (uporabite resitev.args).
Vprašanje 8: Določite vrednosti integracijskih konstant 'C1', 'C2' tako, da v dobljen izraz za pomik vstavite začetna pogoja za pomik in hitrost:
#Začetni pogoji:
x0 = 1
v0 = 0
Vprašanje 9: Dobljeni vrednosti konstant 'C1' in 'C2' vstavite v prej določen izraz pomik.
Dobljeno odvisnost \(x(t)\) izrišite na območju \(0 \leq t \leq 2\) s, pri tem pa parameter w nadomestite z vrednostjo \(2\pi\).
Vprašanje 10: Na 5 mest natančno določite čas t0, ko je obravnavan sistem prvič v ravnovesni legi (\(x(t_0) = 0)\).
Vprašanje 11: Na podlagi končnega izraza za pomike \(x(t)\) tvorite numpy funkcijo za izračun odmika mase od ravnovesne lege v odvisnosti od časa (\(\omega = 2\pi\)).
Izrišite rezultat na obmčju \(0 \leq t \leq 2\) s z uporabo knjižnjice matplotlib.
