7. Osnove naključnih procesov#
Dinamične obremenitve pogosto niso deterministične, ampak imajo lahko v celoti ali delno naključne lastnosti. Primer naključnih obremenitev predstavljajo obremenitve zaradi morskih valov ali hrapavosti ceste. Take obremenitve je treba obravnavati kot naključne procese. V tem poglavju si bomo pogledali, kako naključne obremenitve obravnavamo ter jih potem uspešno uporabimo pri dinamskih sistemih.
Naključni podatki se razlikujejo od determinističnih podatkov, saj jih ni mogoče natančno predvideti. Vendar pa lahko s pomočjo analize segmentov naključnih podatkov razberemo določene značilnosti. Na primer, če merimo hrapavost površine enega segmenta, lahko na podlagi tega z določeno verjetnostjo sklepamo o hrapavosti drugih segmentov. Pri opisu naključnih procesov se pogosto uporablja predpostavka o porazdelitvi procesa, kot je na primer normalna porazdelitev.
Čeprav je mogoče naključni proces analizirati v časovni domeni, pri uporabi takšnega pristopa obstajajo določene pomanjkljivosti. Za ustrezno oceno procesa je treba zbrati dovolj veliko število vzorčnih meritev (ali opazovanj) v časovni domeni, ki jih nato analiziramo kot skupino (ansambel ali ensemble). Kot bomo videli kasneje, pa je analiza strukturne dinamike in naključnih procesov v frekvenčni domeni bistveno elegantnejša.
Priporočamo vam, da si ogledate nekatera referenčna besedila, ki se poglobljeno ukvarjajo z naključnimi procesi:
Nekatere vsebine v tem besedilu so povzete po knjigi Slavič et al. [2020].
Kaj je naključni proces?#
Naključni proces je definiran s kombinacijo funkcije gostote verjetnosti (ang. Probability Density Function \(-\) PDF) in spektralno gostoto moči (ang. Power Spectral Density \(-\) PSD).
Slika spodaj prikazuje ansambel \(\left\{x_k(t)\right\}\) vzorčnih funkcij (opazovanj) \(x_k(t)\), pri čemer je vsako opazovanje \(k\) sestavljeno iz naključne spremenljivke v času \(t_i\): \(x_k(t_i)\). Kot bo podrobneje obravnavano kasneje, predpostavki o stacionarnosti in ergodičnosti bistveno poenostavita analizo naključnih podatkov.
Normalna porazdelitev (Gaussov proces)#
Gaussova porazdelitev je pogosto opažena pri različnih fizikalnih pojavih, njeno razširjenost pa pojasnjuje centralni limitni teorem (Centralni limitni teorem).
Funkcija gostote verjetnosti (PDF) \(p(x)\) za naključni proces \(\left\{x(t_i)\right\}\) definira ob času \(t\) verjetnost amplitude \(x\); za Gaussov proces je PDF definirana kot:
kjer je \(\mu\) povprečna vrednost, \(\sigma\) pa standardni odklon (deviacija) oziroma \(\sigma^2\) varianca. Srednja vrednost \(\mu\) in varianca \(\sigma^2\) določata obliko PDF in se pogosto imenujeta prvi moment in drugi centralni moment; izračunamo ju s pomočjo funkcije gostote verjetnosti:
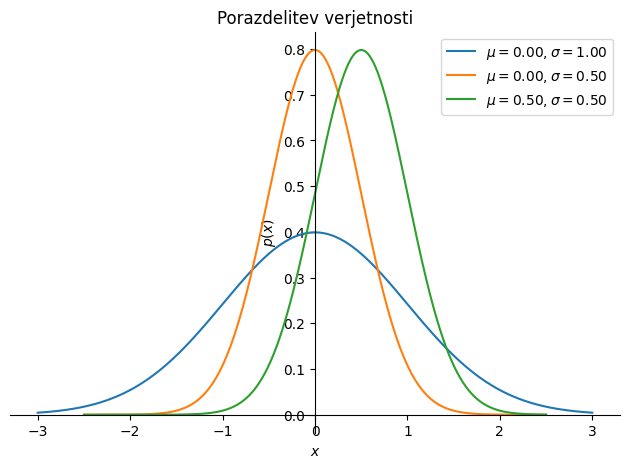
Primer različnih normalnih porazdelitev prikazuje slika spodaj.
Show code cell source
import sympy as sym
σ, μ, x, = sym.symbols('\\sigma, \\mu, x', real=True)
π = sym.pi
p = 1/(σ*sym.sqrt(2*π)) * sym.exp(-(x-μ)**2/(2*σ**2))
podatki = {σ: 1., μ: 0.}
p1 = sym.plot(p.subs(podatki), (x, -3*σ.subs(podatki), +3*σ.subs(podatki)), line_color='C0',
label=f'$\\mu={μ.subs(podatki):3.2f}, \\sigma={σ.subs(podatki):3.2f}$', show=False,
title='Porazdelitev verjetnosti', ylabel='$p(x)$', xlabel='$x$')
podatki = {σ: 0.5, μ: 0.}
p2 = sym.plot(p.subs(podatki), (x, -5*σ.subs(podatki), +5*σ.subs(podatki)), line_color='C1',
label=f'$\\mu={μ.subs(podatki):3.2f}, \\sigma={σ.subs(podatki):3.2f}$', show=False)
podatki = {σ: 0.5, μ: 0.5}
p3 = sym.plot(p.subs(podatki), (x, -5*σ.subs(podatki), +5*σ.subs(podatki)), line_color='C2',
label=f'$\\mu={μ.subs(podatki):3.2f}, \\sigma={σ.subs(podatki):3.2f}$', show=False)
p1.extend(p2)
p1.extend(p3)
p1.legend = True
p1.show()
S spodnjim izračunom lahko preverimo, da sta prvi moment in drugi centralni moment za Gaussovo/normalno porazdelitev dejansko \(\mu\) in \(\sigma^2\):
import sympy as sym
σ, μ, x, = sym.symbols('\\sigma, \\mu, x', real=True, positive=True)
π = sym.pi
p = 1/(σ*sym.sqrt(2*π)) * sym.exp(-(x-μ)**2/(2*σ**2))
m1 = sym.integrate(x*p, (x, -sym.oo, +sym.oo))
cm2 = sym.integrate((x-μ)**2 * p, (x, -sym.oo, +sym.oo))
m1
cm2
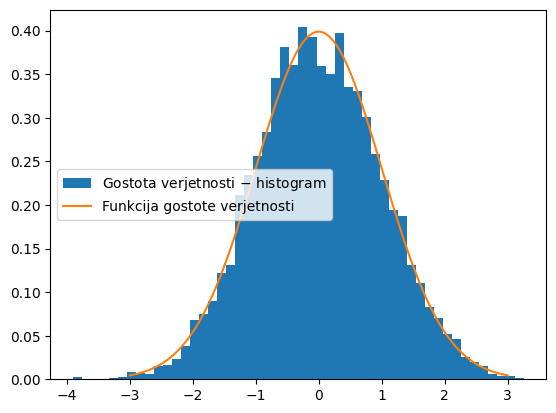
Spodaj je še primer numeričnega generiranja normalne porazdelitve in primerjava s teoretično funkcijo gostote verjetnosti.
Show code cell source
import numpy as np
import matplotlib.pyplot as plt
import sympy as sym
σ, μ, x, = sym.symbols('\\sigma, \\mu, x', real=True, positive=True)
π = sym.pi
p = 1/(σ*sym.sqrt(2*π)) * sym.exp(-(x-μ)**2/(2*σ**2))
podatki = {σ: 1., μ: 0.}
pdf = sym.lambdify(x, p.subs(podatki))
rng = np.random.default_rng(0)
x = rng.normal(loc=podatki[μ], scale=podatki[σ], size=5000)
#x = rng.uniform(low=-1, high=1, size=5000) # enakomerna porazdelitev
plt.plot(x, '.')
plt.xlabel('Naključni dogodek')
plt.ylabel('Vrednost $x$')
plt.show()
plt.hist(x, bins=50, density=True, label='Gostota verjetnosti $-$ histogram')
x = np.linspace(-3*podatki[σ],3*podatki[σ], 100)
plt.plot(x, pdf(x), label='Funkcija gostote verjetnosti')
plt.legend()
plt.show()
Centralni limitni teorem#
Centralni limitni teorem trdi, da vsota neodvisnih naključnih spremenljivk sledi normalni porazdelitvi (ne glede na porazdelitev prvotnih spremenljivk), pod pogojem, da je velikost vzorca dovoljšna.
Spodnja koda demonstrira centralni limitni teorem (ang. Central Limit Theorem \(-\) CLT) z uporabo enakomerno porazdeljenih naključnih spremenljivk. Koda ustvari N = 10 vzorcev, pri čemer ima vsak vzorec k = 5000 naključnih vrednosti, ki sledijo enakomerni porazdelitvi med 0 in 1. Nato izračuna vsoto prvih n vzorcev (n = 1, 2, 5, 10) in prikaže njihove verjetnostne porazdelitve s histogrami. Za vsak histogram je izračunana tudi teoretična normalna porazdelitev z uporabo povprečja in standardne deviacije vsote n vzorcev. Izkaže se, da vsota enakomerno porazdeljenih vzorcev konvergira v normalno porazdelitev.
Show code cell source
import numpy as np
import sympy as sym
import matplotlib.pyplot as plt
seed = 123
rng = np.random.default_rng(seed)
N = 10 # število naključnih vzorcev
k = 5000 # število naključnih vrednosti v vzorcu
data = [rng.uniform(low=0, high=1, size=k) for i in range(N)]
# seštevanje za n = 1, 2, 5 in 10
S1 = np.sum(data[:1], axis=0) # n = 1
S2 = np.sum(data[:2], axis=0) # n = 2
S5 = np.sum(data[:5], axis=0) # n = 5
S10 = np.sum(data[:10], axis=0) # n = 10
σ, μ, x, = sym.symbols('\\sigma, \\mu, x', real=True, positive=True)
π = sym.pi
p = 1/(σ*sym.sqrt(2*π)) * sym.exp(-(x-μ)**2/(2*σ**2)) # teoretična gostota verjetnosti
fig, axs = plt.subplots(2, 2, figsize=(15, 5))
fig.suptitle(r'Seštevek enakomerno porazdeljenih naključnih spremenljivk $-$ verjetnostna porazdelitev')
bins = 25 # število stolpcev za histogram
# graf za n = 1
axs[0, 0].hist(S1, bins=bins, density=True, label='$n=1$')
data = {σ: np.std(S1), μ: np.mean(S1)}
pdf = sym.lambdify(x, p.subs(data))
x_S1 = np.linspace(-3*data[σ]+data[μ], 3*data[σ]+data[μ], 100)
axs[0, 0].plot(x_S1, pdf(x_S1), lw=3, label='Normalna gostota verjetnosti')
axs[0, 0].set_ylabel('$p(x)$')
axs[0, 0].legend(loc='upper right')
# graf za n = 2
axs[0, 1].hist(S2, bins=bins, density=True, label='$n=2$')
data = {σ: np.std(S2), μ: np.mean(S2)}
pdf = sym.lambdify(x, p.subs(data))
x_S2 = np.linspace(-3*data[σ]+data[μ], 3*data[σ]+data[μ], 100)
axs[0, 1].plot(x_S2, pdf(x_S2), lw=3, label='Normalna gostota verjetnosti')
axs[0, 1].set_ylabel('$p(x)$')
axs[0, 1].legend(loc='upper right')
# graf za n = 5
axs[1, 0].hist(S5, bins=bins, density=True, label='$n=5$')
data = {σ: np.std(S5), μ: np.mean(S5)}
pdf = sym.lambdify(x, p.subs(data))
x_S5 = np.linspace(-3*data[σ]+data[μ],3*data[σ]+data[μ], 100)
axs[1,0].plot(x_S5, pdf(x_S5), lw=3, label='Normalna gostota verjetnosti')
axs[1,0].set_xlabel('$x$')
axs[1,0].set_ylabel('$p(x)$')
axs[1,0].legend(loc='upper right')
# graf za n = 10
axs[1,1].hist(S10, bins=bins, density=True, label='$n=10$');
data = {σ: np.std(S10), μ: np.mean(S10)}
pdf = sym.lambdify(x, p.subs(data))
x_S10 = np.linspace(-3*data[σ]+data[μ],3*data[σ]+data[μ], 100)
axs[1,1].plot(x_S10, pdf(x_S10), lw=3, label='Normalna gostota verjetnosti')
axs[1,1].set_xlabel('$x$')
axs[1,1].set_ylabel('$p(x)$')
axs[1,1].legend(loc='upper right');
plt.show()
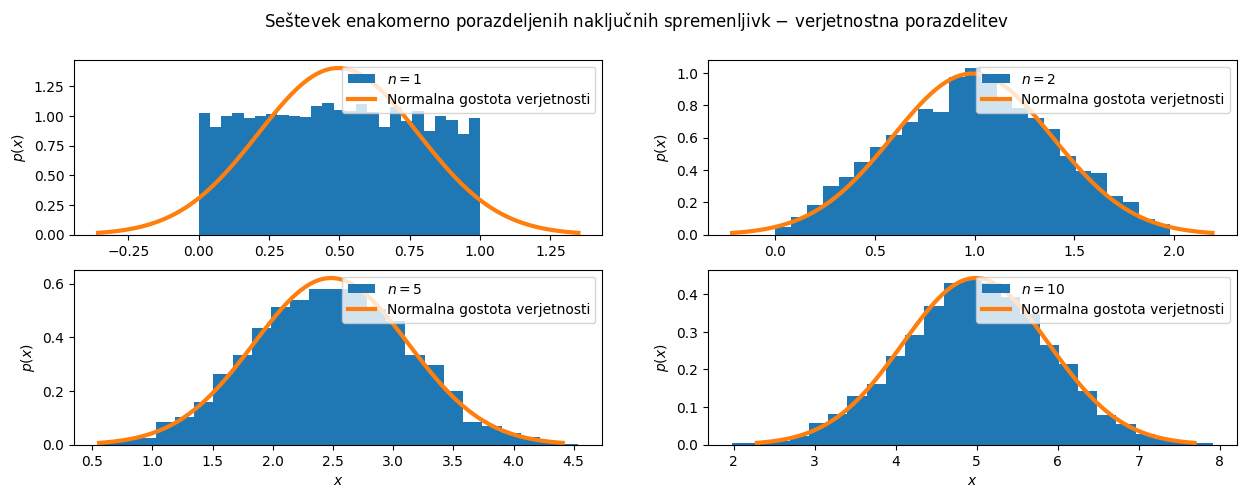
Centralni limitni teorem tudi pravi, da se porazdelitev vzorca povprečij vsake naključne spremenljivke približuje normalni porazdelitvi, ko velikost vzorca narašča, tudi če je prvotna populacija porazdeljena drugače kot normalno. To drži, če so vzorci neodvisni in enako porazdeljeni ter je velikost vzorca dovoljšna.
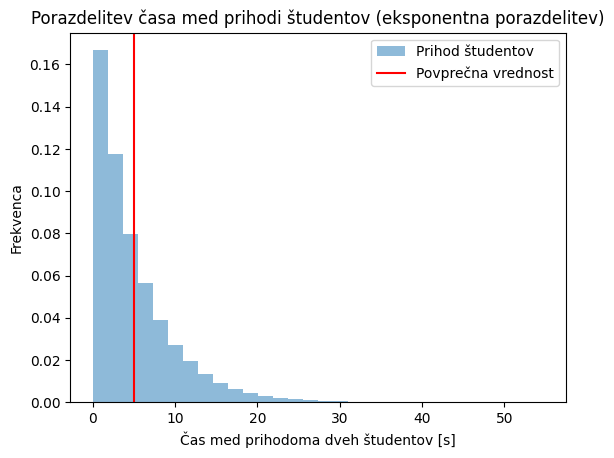
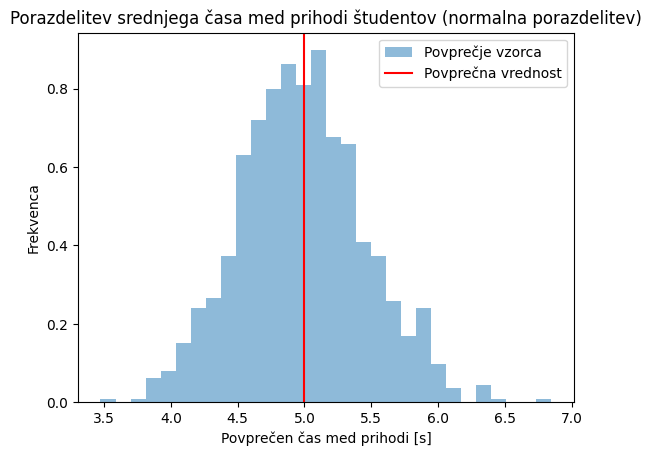
Poglejmo si sedaj še zgled z drugačno porazdelitvijo: spremljali bomo eksponentno porazdeljen čas med prihodoma dveh študentov v učilnico. V kodi spodaj kreiramo zelo velik vzorec: število_študentov = 100000 in opazimo, da večina študentov pride s časovno razliko manj kot 20 s. Naslednja slika prikazuje povprečja vzorcev, kjer smo začetne podatke razdelili v vzorce velikosti: velikost_vzorca = 100. Opazimo, da so povprečja normalno porazdeljena.
Show code cell source
import numpy as np
import matplotlib.pyplot as plt
upad = 0.2
število_študentov = 100000
prihod_študentov = np.random.exponential(scale=1/upad, size=število_študentov)
plt.hist(prihod_študentov, bins=30, density=True, alpha=0.5, label='Prihod študentov')
plt.xlabel('Čas med prihodoma dveh študentov [s]')
plt.ylabel('Frekvenca')
plt.title('Porazdelitev časa med prihodi študentov (eksponentna porazdelitev)')
plt.axvline(x=1/upad, color='r', label='Povprečna vrednost')
plt.legend()
plt.show()
velikost_vzorca = 100
povprečja_vzorcev = np.mean(prihod_študentov.reshape((velikost_vzorca,-1)),axis=0)
plt.hist(povprečja_vzorcev, bins=30, density=True, alpha=0.5, label='Povprečje vzorca')
plt.xlabel('Povprečen čas med prihodi [s]')
plt.ylabel('Frekvenca')
plt.title('Porazdelitev srednjega časa med prihodi študentov (normalna porazdelitev)')
plt.axvline(x=1/upad, color='r', label='Povprečna vrednost')
plt.legend()
plt.show()
Momenti funkcije gostote verjetnosti#
V nadaljevanju si bomo pogledali orodja za popis lastnosti naključnih procesov. Predpostavimo, da imamo dva naključna procesa \(\left\{x_k(t)\right\}\) in \(\left\{y_k(t)\right\}\), kjer je \(k\) indeks ponovitve procesa ob času \(t\). Statistično povprečje celotnega ansambla ponovitev procesa (čez indeks \(k\)) označimo kot \(E[]\) (\(E[]\) označuje pričakovano vrednost/posplošeno povprečje, ang. expected value; glejte tudi povezavo):
Opomba: zgornji zapis pomeni, da se povprečje lahko spreminja s časom \(t\).
Opomba
Zgornji izraz posplošimo tako, da definiramo \(\boldsymbol{n}\)-ti moment funkcije gostote verjetnosti:
Kovariančne funkcije so za dva procesa \(\left\{x_k(t)\right\}\) in \(\left\{y_k(t) \right\}\) definirane kot:
Poseben primer, vreden pozornosti, je pri \(\tau = 0\):
Varianci \(\sigma_x^2(t)\) in \(\sigma_y^2(t)\) sta tako definirani in \(C_{xy}(t)\) je kovarianca med \(\left \{x_k(t)\right\}\) in \(\left\{y_k(t)\right\}\) ob času \(t\).
Če bi analizirali proces z dvodimenzionalno normalno porazdelitvijo, bi bile lastnosti \(\sigma_x^2(t)\), \(\sigma_y^2(t)\) in \(C_{xy}(t)\) dovolj za popis verjetnosti v določenih časovnih točkah \(t\).
Opomba
Zgornji izraz posplošimo, tako da definiramo \(\boldsymbol{n}\)-ti centralni moment funkcije gostote verjetnosti:
Opomba
Za naključna procesa \(\left\{x_k(t)\right\}\) in \(\left\{y_k(t)\right\}\) pravimo, da sta šibko stacionarna, ko so srednje vrednosti in kovariančne funkcije časovno neodvisne. Procesi se štejejo za močno stacionarne, ko so časovno neodvisni tudi statistični momenti višjega reda in križni momenti. Ker je Gaussov proces definiran z dvema statističnima momentoma (funkcijo porazdelitve verjetnosti je mogoče izpeljati samo iz srednjih vrednosti in kovarianc [Newland, 2012]), šibka in močna stacionarnost tu sovpadata.
Opomba
Avtokorelacijska funkcija \(R_{xx}(\tau)\) in križnokorelacijska funkcija \(R_{xy}(\tau)\) se uporabljata za stacionarne naključne procese in sta enaki kovariančnim funkcijam v primeru procesa z ničelno srednjo vrednostjo:
Ergodičnost#
V ergodičnem procesu lahko statistične lastnosti (npr. povprečje ali varianco) namesto čez ansambel opazovanj (\(k\)) določimo na podlagi časovnega razvoja (\(t\)) enega samega opazovanja.
Zgoraj (Momenti funkcije gostote verjetnosti) smo srednjo vrednost določili čez ansambel dogodkov. Ob predpostavki ergodičnosti pa jo lahko določimo na podlagi časovnega povprečja:
Preprosto povedano: če bi 1000 ljudi hkrati vrglo igralno kocko za Človek ne jezi se, bi dobili zelo podoben rezultat, kot če bi ena oseba vrgla kocko 1000-krat. Pri tem moramo predpostaviti, da zaporedni dogodki v času (ko meče ena oseba) niso med seboj povezani (npr. da se kocka s časom ne obrablja). V zgornji enačbi tako opazujemo \(k\)-ti proces v času.
Podobno lahko trdimo za kovariančno funkcijo:
Opomba
Za proces rečemo, da je šibko ergodičen (ang. weakly ergodic), če so časovna povprečja enaka povprečjem ansambla dogodkov, neodvisno od izbranega \(k\):
Če pogoji šibke ergodičnosti veljajo za vse statistične lastnosti višjega reda, je proces močno ergodičen (ang. strongly ergodic). Za Gaussovo porazdelitev pa sta močna in šibka ergodičnost zamenljiva izraza, kot je bilo v primeru stacionarnosti \(-\) prvi moment in drugi centralni moment sta dovolj za enolični opis Gaussove porazdelitve. V takih primerih so statistične lastnosti vsake ločene vzorčne funkcije reprezentativne za celoten ansambel. Pri nadaljnji analizi ergodičnih procesov lahko torej indeks \(k\) izpustimo in vzorčno funkcijo, ki v celoti opisuje lastnosti naključnega procesa, označimo z \(x(t)\).
Ergodičnost je pomembna iz različnih razlogov: poenostavlja nadaljnjo teoretično obravnavo naključnih procesov; še pomembneje pa je, da omogoča analizo dejansko izmerjenih naključnih podatkov. Namesto analize velikega ansambla časovnih zgodovin pri istem času \(t\) običajno zadostuje, da si ogledamo eno samo časovno zgodovino in na podlagi predpostavke ergodičnosti iz nje izluščimo potrebne statistične lastnosti.
V strukturni dinamiki ponavadi predpostavimo, da ima proces ničelno povprečje in je zato varianco \(\sigma_x^2\) mogoče izračunati na različne načine:
V zgornjih izrazih je predpostavljeno, da \(x(t)\) predstavlja periodične podatke s periodo \(T\). S \(S_{xx}(f)\) smo označili spektralno gostoto moči (ang. power spectral density) in smo se v tej vrstici naslonili na Parsevalov teorem (glejte poglavje Parsevalov teorem in močnostni spekter). Spektralno gostoto moči si bomo podrobneje pogledali v naslednjem poglavju. Opomba: če obravnavamo normalno porazdeljeni proces z ničelno srednjo vrednostjo, je varianca edini manjkajoči parameter, ki tako porazdelitev enolično določi.
Gostota močnostnega spektra (ang. Power Spectral Density, PSD)#
Gostota močnostnega spektra opisuje frekvenčno gostoto moči naključnega procesa in dopolnjuje funkcijo gostote verjetnosti (\(p(x)\)) pri definiciji določenega naključnega procesa; ista gostota verjetnosti ima lahko v frekvenčni domeni zelo različne gostote močnostnega spektra (PSD). PSD ponavadi pridobimo s Fourierovo transformacijo, običajno z uporabo algoritma FFT.
Definicija PSD temelji na avtokorelacijski funkciji \(R_{xx}(\tau)\), ki implicitno vsebuje frekvenčno vsebino \(x(t)\), hkrati pa izpolnjuje Dirichletov pogoj (vsaj v primeru procesov z ničelno srednjo vrednostjo):
Ker sta avtokorelacijska funkcija in PSD par Fourierove transformacije, lahko za naključna procesa \(x(t)\) in \(y(t)\) zapišemo naslednje (Wiener-Khinchine) odnose:
\(S_{xx}(f)\) in \(S_{yy}(f)\) (PSD, imenovana tudi avtospektralna gostota) sta sodi funkciji s pozitivnimi realnimi vrednostmi. Križnospektralna gostota (tudi CSD, Cross-Spectral Density) \(S_{xy}(f)\) ima v splošnem kompleksne vrednosti.
Poglejmo si najprej avtospektralno gostoto:
Na podoben način bi lahko izpeljali križnospektralno gostoto \(S_{xy}\).
V primeru realnih meritev je časovna zgodovina končne dolžine in je izpolnjen Dirichletov pogoj; iz Fourierove transformacije \(k\)-te časovne zgodovine:
lahko z množenjem Fourierovih transformirank določimo križnospektralno gostoto (ker imamo končno dolgi signal, moramo, da dobimo gostoto, normirati na \(T\)):
Opomba
Avto- (PSD) in križnospektralna (CSD) gostota močnostnega spektra sta torej za primer ergodičnega procesa definirani kot (brez indeksa \(k\)):
Avtospektralna gostota \(S_{xx}(f)\) pokriva negativne in pozitivne frekvence in se zato imenuje tudi dvostranska funkcija spektralne gostote. Pogosto se uporablja enostranska funkcija spektralne gostote \(G_{xx}(f)\), ki je definirana kot:
Podobno velja za \(G_{xy}(f)\). Za dvostransko križnospektralno gostoto velja \(S_{xy}(f)=S_{yx}^*(f)\).
Zgled 1#
Poglejmo si najprej izračun avtospektralne gostote s pomočjo Fourierove transformacije. Na koncu zgleda preverimo Parsevalov teorem v diskretni obliki:
Pri zgledu bodite previdni, kako se obravnava \(S_{xx}(f)\) in \(G_{xx}(f)\).
Show code cell source
import numpy as np
from scipy.signal import welch
import matplotlib.pyplot as plt
rng = np.random.default_rng(0)
N = 5000
fs = 1000
dt = 1./fs
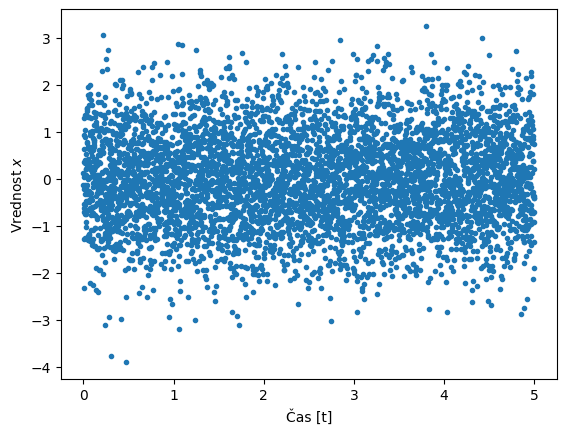
x = rng.normal(size=N)
time = np.arange(N)*dt
T = dt*N
plt.plot(time, x, '.')
plt.xlabel('Čas [t]')
plt.ylabel('Vrednost $x$')
plt.show()
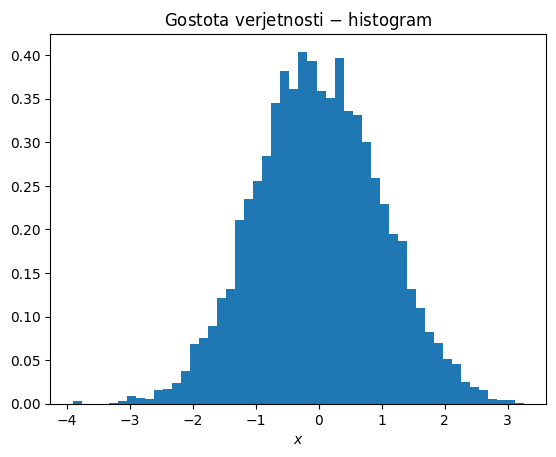
plt.title('Gostota verjetnosti $-$ histogram')
plt.xlabel('$x$')
plt.hist(x, bins=50, density=True)
plt.show()
X = np.fft.fft(x)/N
freq = np.fft.fftfreq(N, d=dt)
scale = 1.0 * N / fs # skaliranje na gostoto
Sxx = X.conj()*X * scale
X_r = np.fft.rfft(x)/N
freq_r = np.fft.rfftfreq(N, d=dt)
Gxx = 2*X_r.conj()*X_r * scale
# alternativen izračun prek Scipy (tako se dejansko dela pozneje)
freq2, Gxx2 = welch(x, window=np.ones_like(x), fs=fs)
plt.title('Avtospektralna gostota')
plt.semilogy(freq, np.abs(Sxx), alpha=0.5, label='$S_{xx}$')
plt.semilogy(freq2, np.abs(Gxx2), alpha=0.5, label='$G_{xx}$')
plt.ylim(1e-8,1e0)
plt.legend()
plt.xlabel('Frekvenca [Hz]')
plt.ylabel('$S_{xx}$')
plt.show()
print('Integral v času: ', np.trapezoid(x*x, dx=dt)/(N/fs),
'\nIntegral PSD (Sxx): ', np.trapezoid(np.real(Sxx), dx=1/(N/fs)),
'\nIntegral PSD (Gxx): ', np.trapezoid(np.real(Gxx), dx=1/(N/fs)),
'\nIntegral PSD (Gxx) Welch: ', np.trapezoid(np.real(Gxx2), dx=1/(N/fs)))
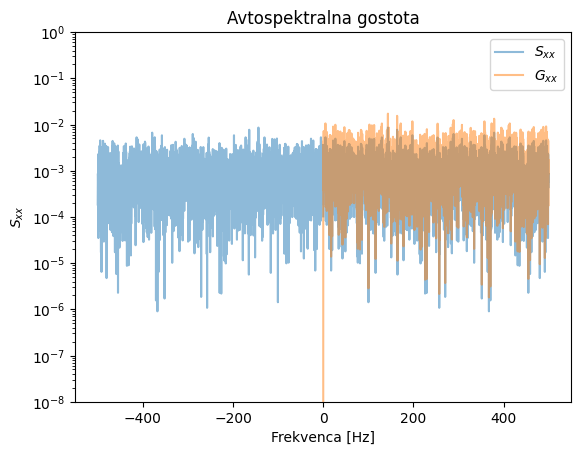
Integral v času: 0.9904720416233659
Integral PSD (Sxx): 0.9906062124167659
Integral PSD (Gxx): 0.9908307702229943
Integral PSD (Gxx) Welch: 0.9907922407740426
Pogledamo lahko tudi izračun variance z vgrajeno numpy.var() metodo:
np.var(x)
np.float64(0.9908102289544899)
Do majhnih razlik pride, ker smo v naši kodi predpostavili (np.var te predpostavke ne naredi), da ima časovna vrsta x srednjo vrednost nič, kar pa ni povsem res:
np.mean(x)
np.float64(-0.004532247621656686)
Zgled 2#
Poglejmo si sedaj zgled in najprej izračunajmo varianco s pomočjo definicije normalne porazdelitve z ničelno srednjo vrednostjo \(\mu=0\) in standardno deviacijo \(\sigma=3\):
import sympy as sym
σ, μ, x, = sym.symbols('\\sigma, \\mu, x', real=True, positive=True)
π = sym.pi
p = 1/(σ*sym.sqrt(2*π)) * sym.exp(-(x-μ)**2/(2*σ**2))
podatki = {σ: 3., μ: 0.}
sym.integrate(x**2*p, (x, -sym.oo, +sym.oo)).subs(podatki)
Pridobili smo pričakovano vrednost \(\sigma^2=9\). Nadaljujemo z integriranjem časovne vrste v času:
import numpy as np
σ = 3
rng = np.random.default_rng(0)
N = 1_000_000
T = 10
time, dt = np.linspace(0, T, N, retstep=True)
fs = 1/dt
x = rng.normal(scale=σ, size=N)
np.trapezoid(x**2, dx=dt)/T
np.float64(9.01211481059612)
Ker gre za numerične podatke, smo pridobili vrednost, ki je bolj ali manj blizu pričakovani vrednosti \(\sigma^2=9\) (poskusite spremeniti N). Nadaljujemo z izračunom variance v frekvenčni domeni:
Ali z uporabo enostranskega amplitudnega spektra:
X = np.fft.fft(x)/N
scale = 1/(fs*N)
Sxx = np.real(X.conj()*X) * scale
np.sum(Sxx)*fs*N
np.float64(9.012106104865358)
X_r = np.fft.rfft(x)/N
scale = 1/(fs*N)
Gxx = np.real(X_r.conj()*X_r) * scale
Gxx[1:] = 2*Gxx[1:]
np.sum(Gxx)*fs*N
np.float64(9.012110027353884)
Spektralni momenti#
Iz definicije PSD sledi, da je površina pod krivuljo enaka pričakovani kvadratni vrednosti \(E[x^2]\) procesa (glejte poglavje Parsevalov teorem in močnostni spekter):
kjer je \(m_0\) ničelni spektralni moment enak varianci \(\sigma_x^2\) procesa ničelne srednje vrednosti. Višji sodi momenti ustrezajo varianci časovnih odvodov prvotnega naključnega procesa:
Splošni izraz za \(i\)-ti spektralni moment \(m_i\) lahko zapišemo v obliki:
kjer je \(G_{xx}\) enostranski PSD.
Treba je poudariti, da moramo \(-\) če je PSD podan v Hz (\(G_{xx}(f)\)) \(-\) paziti na pravilno uporabo ročice \((2\pi\,f)^i\):
Zgled#
Ponovno si poglejmo zgled; najprej definirajmo harmonski odziv z amplitudo \(A=1\). Varianca pomika je pričakovana: \((A/\sqrt{2})^2=0.5\,A\), varianca hitrosti pa: \(((2\pi\,f_0\,A)/\sqrt{2})^2=2\pi^2\,f_0^2\,A\) in varianca pospeška: \((((2\pi\,f_0)^2\,A)/\sqrt{2})^2=2^3(\pi\,f_0)^4\,A\).
Show code cell source
import numpy as np
import matplotlib.pyplot as plt
N = 1_000_000
T = 10
f_0 = 100
time, dt = np.linspace(0, T, N, retstep=True)
x = np.sin(2*np.pi*f_0*time)
X = np.fft.rfft(x)/N
freq = np.fft.rfftfreq(N, dt)
plt.title('Prvih 5000 točk determinističnega signala')
plt.plot(time[:5000], x[:5000])
plt.xlabel('$t$ [s]')
plt.ylabel('$x$')
np.trapezoid(x**2, dx=dt)/T
np.float64(0.5000000000000002)
Definirajmo funkcijo spektralnih momentov:
def spektralni_moment(X_r, freq, i=0):
# scale tukaj ne uporabimo, ker se pokrajša
Gxx = X_r.conj()*X_r
Gxx[1:] = 2*Gxx[1:]
return np.real(np.sum((2*np.pi*freq)**i * Gxx))
Spektralni moment \(m_0\) (pomik): preverimo, ali res dobimo pričakovano vrednost (\(0.5\,A=0.5\)) tudi v frekvenčni domeni:
spektralni_moment(X_r=X, freq=freq, i=0)
np.float64(0.49999950000000004)
Spektralni moment \(m_2\) (hitrost): za hitrost pričakujemo vrednost \(2\,\pi^2\,f_0^2\,A=197392.08\):
spektralni_moment(X_r=X, freq=freq, i=2)
np.float64(197392.04313357425)
Ali v času:
v = np.gradient(x)/dt
np.trapezoid(v**2, dx=dt)/T
np.float64(197389.49045450424)
Spektralni moment \(m_4\) (pospešek): za pospešek pričakujemo \(2^3(\pi\,f_0)^4\,A=77927272827.2\):
spektralni_moment(X_r=X, freq=freq, i=4)
np.float64(100537876580.7631)
Ali v času:
a = np.gradient(v)/dt
np.trapezoid(a**2, dx=dt)/T
np.float64(77925221885.31581)
Opazimo že relativno veliko odstopanje, razlog je v numerični napaki. Amplitudni spekter \(X\) ima zunaj \(f_0\) teoretično vrednost 0, dejansko vrednost pa blizu 0; ker izraz za izračun četrtega spektralnega momenta visoke frekvence zelo poudari (\((2\pi\,f)^4\)), se poudari tudi numerična napaka. Boljši rezultat pridobimo, če se npr. frekvenčno omejimo:
sel = np.logical_and(freq>=(f_0-1),freq<=(f_0+1))
spektralni_moment(X_r=X[sel], freq=freq[sel], i=4)
np.float64(77926867176.11658)
