Ctrl+K

6. Diskretna Fourierova transformacija

6. Diskretna Fourierova transformacija#

Prej smo spoznali Fourierovo transformacijo za vzorčene podatke (glejte poglavje Enakomerno časovno vzorčenje), kjer vzorčimo s korakom \(\Delta t\,n\) in \(n\in\mathbb{Z}\) gre od \(-\infty\) do \(+\infty\). Kadar imamo končno mnogo vzorčenih podatkov (\(N\)) in gre \(n=[0,1,\dots,N-1]\), uporabimo diskretno Fourierovo transformacijo (DFT).

Opomba

Diskretna Fourierova transformacija:

\[ X_k = \sum_{n=0}^{N-1} x_n\,\mathrm{e}^{-\mathrm{i}\,2\pi\,k\,n/N}, \]

kjer velja \(x_n = x(n\,\Delta t)\) in \(X_k=X(k/(N\,\Delta t))\). Ker je DFT periodična z \(1/\Delta t\) (\(X_k=X_{k+N}\)), je treba izračunati samo \(N\) členov, torej \(k=[0,1,\dots\,N-1]\).

Da velja \(X_k=X_{k+N}\), dokažemo z:

\[ \mathrm{e}^{-\mathrm{i}\,2\pi\,k\,n/N}=\mathrm{e}^{-\mathrm{i}\,2\pi\,n\,(k+N)/N}=\mathrm{e}^{-\mathrm{i}\,2\pi\,n\,k/N}\,\underbrace{\mathrm{e}^{-\mathrm{i}\,2\pi\,n\,N/N}}_{=\cos(-2\pi\,n)=1}. \]

Inverzno DFT izpeljemo, tako da zgornjo enačbo pomnožimo z \(\mathrm{e}^{\mathrm{i}\,2\pi\,k\,r/N}\) in nato seštejemo po \(k\):

\[ \sum_{k=0}^{N-1}X_k\,\mathrm{e}^{\mathrm{i}\,2\pi\,k\,r/N} = \sum_{k=0}^{N-1}\sum_{n=0}^{N-1} x_n\,\mathrm{e}^{-\mathrm{i}\,2\pi\,k\,n/N}\,\mathrm{e}^{\mathrm{i}\,2\pi\,k\,r/N}, \]

nato na desni strani zamenjamo vrstni red vsote in ugotovimo:

\[\begin{split} \sum_{k=0}^{N-1} \mathrm{e}^{-\mathrm{i}\,2\pi\,k\,(n-r)/N}= \begin{cases} N; &\quad n=r,\\ 0 &\quad\textrm{sicer.} \end{cases} \end{split}\]

Sledi:

\[ \sum_{k=0}^{N-1}X_k\,\mathrm{e}^{\mathrm{i}\,2\pi\,k\,r/N} = x_r\,N. \]

Opomba

Inverzna diskretna Fourierova transformacija:

\[ x_n = \frac{1}{N} \sum_{k=0}^{N-1} X_k\,\mathrm{e}^{\mathrm{i}\,2\pi\,k\,n/N}, \]

ker velja:

\[ \mathrm{e}^{\mathrm{i}\,2\pi\,k\,n/N}=\mathrm{e}^{\mathrm{i}\,2\pi\,k\,(n+N)/N}=\mathrm{e}^{\mathrm{i}\,2\pi\,k\,n/N}\,\underbrace{\mathrm{e}^{\mathrm{i}\,2\pi\,k\,N/N}}_{=\cos(2\pi\,k)=1}. \]

Opomba

Ugotovimo, da je \(x_n\) periodična vrsta \(x_n=x_{n+N}\). Res smo začeli z vzorčenimi podatki v času \(x_n\), ki niso periodični; rezultat z inverzno DFT pa je periodičen.

Hitra Fourierova transformacija#

Hitra Fourierova transformacija (ang. Fast Fourier Transform \(-\) FFT) je ime numeričnega algoritma za diskretno Fourierovo transformacijo. DFT ima numerični obseg proporcionalen z \(N^2\), kar zapišemo kot \(\mathcal{O}(N^2)\). Za avtorja hitre Fourierove transformacije veljata James Cooley in John Tukey, ki sta algoritem objavila leta 1965 (glejte vir), pozneje pa se je izkazalo, da je podoben algoritem že bistveno prej, v neobjavljenem delu iz leta 1805, odkril Carl Friedrich Gauss. Algoritem je, glede na DFT, numerično bistveno hitrejši: \(\mathcal{O}(N\log(N))\); ker numerični obseg s številom elementov \(N\) ne narašča kvadratično, je to bistveno povečalo uporabnost DFT. Nekateri algoritem FFT smatrajo kot enega najpomembnejših algoritmov, saj je imel (in še ima) zelo pomemben družbeno-ekonomski vpliv. Kot zanimivost lahko tukaj povemo, da algoritem ni bil patentiran (glejte vir). Zaradi simetrije v podatkih je hitrost izračuna najvišja, če je število vzorcev enako \(2^n\), kjer \(n\in\mathbb{Z}\).

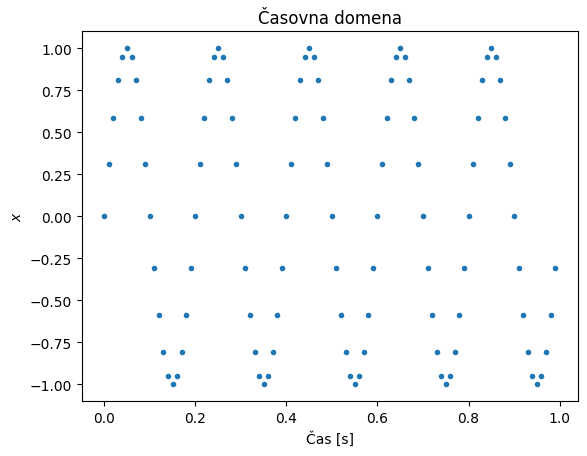
Diskretna Fourierova transformacija je v paketu numpy dokumentirana tukaj in si jo bomo najprej pogledali na spodnjem primeru sinusoide z amplitudo A, frekvenco fr, frekvenco vzorčenja fs in dolžino vzorčenja N, ki bo enaka frekvenci vzorčenja (vzorčili bomo torej 1 sekundo). DFT bomo izvedli z metodo numpy.fft.fft() (dokumentacija).

import numpy as np

A = 1
fr = 5
fs = 100 
N = 100
dt = 1/fs
t = np.arange(N)*dt
x = A*np.sin(2*np.pi*fr*t)

X = np.fft.fft(x)
freq = np.fft.fftfreq(len(x), d=dt)

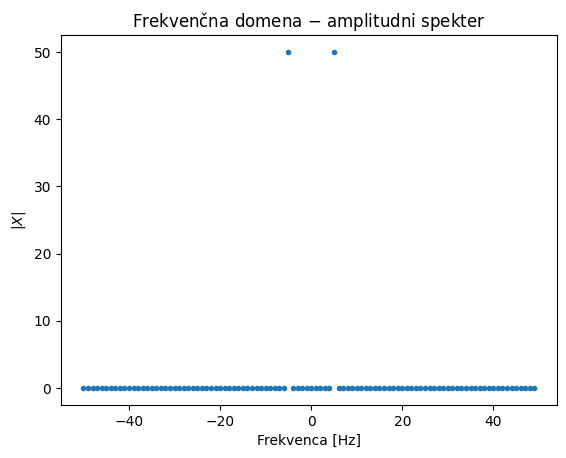
Sinusoida ima samo eno frekvenčno komponento različno od nič:

(X[freq==fr], np.abs(X[freq==fr]))

(array([-1.62040942e-14-50.j]), array([50.]))
Hide code cell source 
import matplotlib.pyplot as plt

plt.title('Časovna domena')
plt.plot(t, x, '.')
plt.xlabel('Čas [s]')
plt.ylabel('$x$')
plt.show()

plt.title('Frekvenčna domena $-$ amplitudni spekter')
plt.plot(freq, np.abs(X), '.')
plt.xlabel('Frekvenca [Hz]')
plt.ylabel('$|X|$')
plt.show()
../_images/cf6effb2703e2b10b08531266f2689e241c661abbdc06c6c9c2cc755d7424ce7.png ../_images/ad7ace5e1471632cd86bd649b279e383058e39b1dfa51d9b5cbc841c02ecb007.png

Fourierove vrste in diskretna Fourierova transformacija#

Diskretna Fourierova transformacija je s Fourierovimi vrstami zelo povezana. Povezavo lahko hitro razkrijemo, če predpostavimo diskretno časovno vrsto \(x_i=x(\Delta t\,i)\), kjer je \(\Delta t\) konstanten časovni korak, \(i=0,1,\dots,N-1\) in \(T_p=N\,\Delta t\); sledi:

\[\begin{split} \begin{split} c_k &= \frac{1}{T_p}\,\int_0^{T_p} x(t)\,\mathrm{e}^{-\mathrm{i}\,2\pi\,k\,t/T_p}\,\mathrm{d}t\\ &= \frac{1}{N\,\Delta t}\,\sum_{n=0}^{N-1} x(n\,\Delta t)\,\mathrm{e}^{-\mathrm{i}\,2\pi\,k\,\Delta t\,n/(N\,\Delta t)}\,\Delta t\\ &= \frac{1}{N}\,\underbrace{\sum_{n=0}^{N-1} x(n\,\Delta t)\,\mathrm{e}^{-\mathrm{i}\,2\pi\,k\,n/N}}_{X_k}\\ &= \frac{X_k}{N}.\\ \end{split} \end{split}\]

Poudariti je treba, da v splošnem velja \(X_k/N\ne c_k\), saj DFT temelji na končni vrsti in je zato \(X_k\) periodična vrsta.

Pri primerjanju DFT in Fourierovih vrst pogosto pride do napake pri razumevanju periode (predvsem zadnje diskretne točke). V zgornjem primeru sinusoide časovna točka pri t = 1 eksplicitno ni vključena; implicitno pa je, saj smo zgoraj spoznali, da so vzorčeni podatki periodični in velja \(x_n=x_{n+N}\). Poglejmo ta detajl pobliže; členi Fourierove vrste so definirani kot:

\[ c_n = \frac{1}{T_p}\,\int_0^{T_p} x(t)\,\mathrm{e}^{-\mathrm{i}\,2\pi\,n\,t/T_p}\,\mathrm{d}t. \]

Izračunamo Fourierov koeficient za frekvenco fr:

import sympy as sym

t, fr, Tp, A = sym.symbols('t, fr, Tp, A')
π = sym.pi
i = sym.I

podatki = {fr: 5, A:1, Tp:1}

x = sym.sin(2*π*fr*t)
c = 1/Tp*sym.integrate(x*sym.exp(-i*2*π*fr*t/Tp), (t,0,Tp))

c.subs(podatki)
\[\displaystyle - \frac{i}{2}\]

Do istega rezultata pridemo prek DFT, vendar zadnja časovna točka eksplicitno ni vključena:

import numpy as np

A = 1
fr = 5
fs = 100 
N = 100
# Spodnja `fs` rezultira v vključenost zadnje točke. Rezultat bo napačen!
#fs = 100/1.01010101010101
dt = 1/fs
t = np.arange(100)*dt
x = A*np.sin(2*np.pi*fr*t)

X_r = np.fft.rfft(x)
freq_r = np.fft.rfftfreq(len(x), d=dt)

c = X_r[freq_r==fr] / len(x)
c

array([-1.49438567e-16-0.5j])

Prepričajmo se, da zadnja časovna točka eksplicitno ni vključena:

t[-3:]

array([0.97, 0.98, 0.99])

Če v kodi zgoraj spremenimo fs ali število točk, tako da je zadnja točka eksplicitno vključena, rezultat ne bo enak tistemu iz Fourierovih vrst!

Frekvenčna ločljivost in dodajanje ničel#

Frekvenčna ločljivost DFT je definirana z dolžino diskretne časovne vrste \(x_i=x(\Delta t\,i)\), kjer je \(\Delta t\) konstanten časovni korak, \(i=0,1,\dots,N-1\); dolžina take vrste je torej \(T_p=N\,\Delta t\), zato sledi, da je frekvenčna ločljivost:

\[ \Delta f= \frac{1}{N\,\Delta t}. \]

Z daljšo časovno vrsto bi lahko imeli tudi boljšo frekvenčno ločljivost. Kadar dodatnih točk diskretne vrste ne moremo pridobiti, lahko frekvenčno ločljivost povečamo z dodajanjem ničel:

\[\begin{split} \tilde{x}_n= \begin{cases} x_n;\quad & 0\le n\le N-1,\\ 0;\quad & N\le n\le L-1. \end{cases} \end{split}\]

Sledi:

Opomba

diskretna Fourierova transformacija z dodajanjem ničel (ang. zero-padding):

\[ \tilde{X}_k = \sum_{n=0}^{L-1} \tilde{x}_n\,\mathrm{e}^{-\mathrm{i}\,2\pi\,k\,n/L} = \sum_{n=0}^{N-1} x_n\,\mathrm{e}^{-\mathrm{i}\,2\pi\,k\,n/L}. \]

Na takšen način pridobimo frekvenčno ločljivost:

\[ \Delta f = \frac{1}{L\,\Delta t}, \]

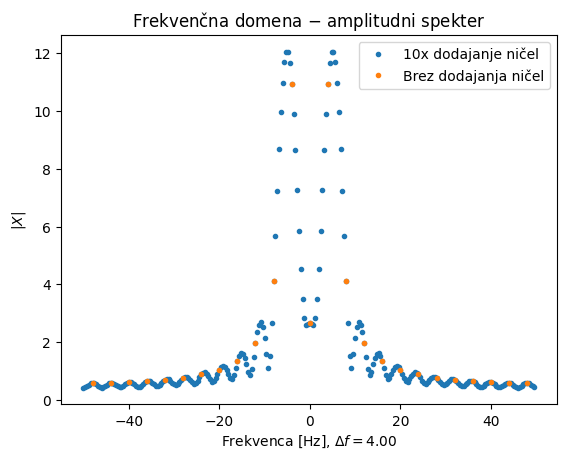
pri tem pa je treba poudariti, da gre samo za frekvenčno interpolacijo, ki nam omogoča podrobnejši vpogled; novih informacij z dodajanjem ničel ne dodajamo. Podobno kakor pri DFT, lahko ničle dodajamo v frekvenčni domeni in nato z inverzno diskretno Fourierovo transformacijo pridobimo bolj goste (interpolirane) časovne podatke.

Pri dodajanju ničel je potrebno paziti na normiranje podatkov; dodanih ničel namreč ne upoštevamo pri normiranju.

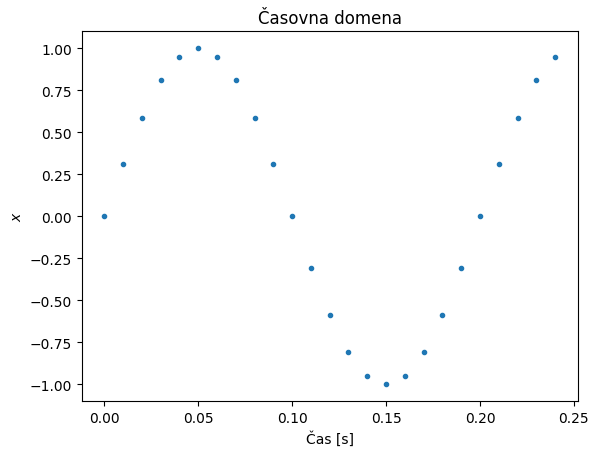
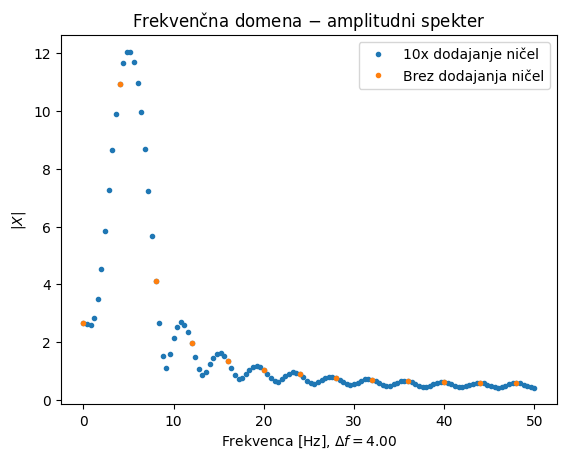
Spodnji primer prikazuje uporabo dodajanja ničel; s pomočjo komentarjev v kodi raziščite delovanje.

Hide code cell source 
import numpy as np
import matplotlib.pyplot as plt


A = 1
fr = 5
fs = 100 
N = 25 # tukaj poskusite z 20 (sinusoida se zaključi; rezultat brez dodajanja ničel je točen!)
k = 10 # dodajanje ničel
dt = 1/fs
t = np.arange(N)*dt
x = A*np.sin(2*np.pi*fr*t)

X = np.fft.fft(x)
freq = np.fft.fftfreq(len(x), d=dt)

X_kx = np.fft.fft(x, n=k*N)
freq_kx = np.fft.fftfreq(k*N, d=dt)


plt.title('Časovna domena')
plt.plot(t, x, '.')
plt.xlabel('Čas [s]')
plt.ylabel('$x$')
plt.show()

plt.title('Frekvenčna domena $-$ amplitudni spekter')
plt.plot(freq_kx, np.abs(X_kx), '.', label=f'{k}x dodajanje ničel')
plt.plot(freq, np.abs(X), '.', label='Brez dodajanja ničel')
plt.xlabel(f'Frekvenca [Hz], $\\Delta f=${1/(N*dt):3.2f}')
plt.ylabel('$|X|$')
plt.legend()
plt.show()
../_images/78cdb5b54665d9c01ecbed88d815c74c2d8701934a30c24cd5b57e8f0f6e7ce0.png ../_images/4874c758ca9801f4b1bfd089b819af945edd47ea9824f564e26eddbcad10db98.png

Simetrija DFT za realne podatke#

Opomba

Za realne podatke v frekvenčni domeni velja:

\[\begin{split} \begin{split} \textrm{Re}\big(X(k)\big)&=\textrm{Re}\big(X(N-k)\big),\\ \textrm{Im}\big(X(k)\big)&=-\textrm{Im}\big(X(N-k)\big),\\ |X(k)|&=|X(N-k)|,\\ \angle X(k)&=\angle X(N-k). \end{split} \end{split}\]

Ker je večina inženirskih podatkov v časovni domeni realnih, je smiselno, da se uporabi ustrezno prilagojena metoda hitre Fourierove transformacije; ta je v paketu numpy dostopna prek klica numpy.fft.rfft(). Inverzna DFT je dosegljiva prek metod numpy.fft.ifft oz. numpy.fft.irfft v primeru realnih podatkov v časovni domeni.

Navedene lastnosti preverimo na kodi v paketu numpy (opomba: k časovnim signalom dodamo šum, da ni faza zelo blizu 0):

import numpy as np

A = 1
fr = 5
fs = 100 
N = 10
dt = 1/fs
t = np.arange(N)*dt
np.random.seed(0)
x = A*np.sin(2*np.pi*fr*t) + np.random.normal(scale=A/2, size=N)

X = np.fft.fft(x)
freq = np.fft.fftfreq(len(x), d=dt)

X_r = np.fft.rfft(x)
freq_r = np.fft.rfftfreq(len(x), d=dt)

np.testing.assert_allclose(freq[1:N//2], -freq[:N//2:-1])
np.testing.assert_allclose(np.real(X[1:N//2]), np.real(X[:N//2:-1]))
np.testing.assert_allclose(np.imag(X[1:N//2]), -np.imag(X[:N//2:-1]))

np.testing.assert_allclose(np.abs(freq[:N//2+1]), freq_r)
np.testing.assert_allclose(np.real(X[:N//2+1]), np.real(X_r))
np.testing.assert_allclose(np.imag(X[:N//2+1]), np.imag(X_r), atol=1e-15)

Še zgornji primer z numpy.fft.rfft():

Hide code cell source 
import numpy as np
import matplotlib.pyplot as plt


A = 1
fr = 5
fs = 100 
N = 25 # tukaj poskusite z 20 (sinusoida se zaključi; rezultat brez dodajanja ničel je točen!)
k = 10 # dodajanje ničel
dt = 1/fs
t = np.arange(N)*dt
x = A*np.sin(2*np.pi*fr*t)

X = np.fft.rfft(x)
freq = np.fft.rfftfreq(len(x), d=dt)

X_kx = np.fft.rfft(x, n=k*N)
freq_kx = np.fft.rfftfreq(k*N, d=dt)


plt.title('Časovna domena')
plt.plot(t, x, '.')
plt.xlabel('Čas [s]')
plt.ylabel('$x$')
plt.show()

plt.title('Frekvenčna domena $-$ amplitudni spekter')
plt.plot(freq_kx, np.abs(X_kx), '.', label=f'{k}x dodajanje ničel')
plt.plot(freq, np.abs(X), '.', label='Brez dodajanja ničel')
plt.xlabel(f'Frekvenca [Hz], $\\Delta f=${1/(N*dt):3.2f}')
plt.ylabel('$|X|$')
plt.legend()
plt.show()
../_images/78cdb5b54665d9c01ecbed88d815c74c2d8701934a30c24cd5b57e8f0f6e7ce0.png ../_images/a62ceca3ebd946a1e25f455976b25a7b7072bd956134f21124a6edadaed2a56f.png

Konvolucija periodičnih podatkov#

Konvolucijo funkcij v primeru Fourierove integralske transformacije smo obravnavali v poglavju Konvolucija funkcij, tukaj si bomo pogledali posebnosti pri obravnavi dveh periodičnih vrst (glejte poglavje Identifikacija harmonskih signalov, ki sestavljajo periodični signal) enake dolžine: \(x_n\) in \(y_n\):

\[ X_k = \sum_{n=0}^{N-1} x_n\,\mathrm{e}^{-\mathrm{i}\,2\pi\,k\,n/N}, \]
\[ Y_k = \sum_{n=0}^{N-1} y_n\,\mathrm{e}^{-\mathrm{i}\,2\pi\,k\,n/N}. \]

Podobno kakor za funkcije, velja tudi za periodične časovne vrste, da je DFT konvolucije v časovni domeni produkt frekvenčnih transformirank.

Opomba

Konvolucija periodičnih podatkov (tudi krožna konvolucija, ang. circular convolution):

\[ \textrm{DFT}\big\{x_n*y_n\big\}=X_k\,Y_k. \]

Da se poudari, da gre za krožno konvolucijo, se kdaj uporabi tudi znak \(\circledast\): \(x_n\circledast y_n\).

Poudarjanje periodičnosti \(x_n\) in \(y_n\) je nujno, sicer (krožna) konvolucija ni mogoča; to bo jasno iz sledeče izpeljave:

\[\begin{split} \begin{split} \textrm{DFT}\big\{x_n\circledast y_n\big\}&=\textrm{DFT}\big\{\sum_r^{N-1}x_r\,y_{n-r}\big\}\\ &=\sum_n^{N-1}\sum_r^{N-1}x_r\,y_{n-r}\,\mathrm{e}^{-\textrm{i}\,2\pi\,n\,k/N}\\ &=\underbrace{\sum_r^{N-1}x_r\,\,\mathrm{e}^{-\textrm{i}\,2\pi\,r\,k/N}}_{X_k}\,\underbrace{\sum_n^{N-1}y_{n-r}\,\mathrm{e}^{-\textrm{i}\,2\pi\,(n-r)\,k/N}}_{Y_k}\\ &=X_k\,Y_k. \end{split} \end{split}\]

Pri zgornji izpeljavi je treba poudariti, da vsota po \(r\) v predzadnji vrstici vključuje tudi vsoto po \(n\), ker pa je vsota po \(n\) zaradi periodičnosti neodvisna od \(r\), se lahko vsoti po \(r\) in \(n\) izvedeta neodvisno. Zaradi periodičnosti \(y_n\) za vsak \(r\) torej velja:

\[ \sum_n^{N-1}y_{n-r}\,\mathrm{e}^{-\textrm{i}\,2\pi\,(n-r)\,k/N}=\sum_n^{N-1}y_{n}\,\mathrm{e}^{-\textrm{i}\,2\pi\,n\,k/N}=Y_k. \]

Če vrsti \(x_n\) in \(y_n\) ne bi bili periodični, konvolucija končnih vrst ne bi bila tako enostavna.

Vsebina