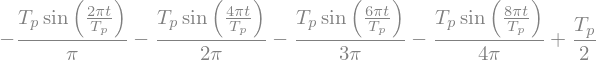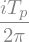2. Fourierove vrste

Vsebina

2. Fourierove vrste#

Cilj Fourierovih vrst je, da bi poljuben (periodični) signal opisali z vsoto harmonskih signalov različnih osnovnih period. V tem poglavju se bomo omejili na matematično definirane signale, in sicer v sledečih korakih:

korak: zapis periodičnega signala kot vsote harmonskih signalov,
korak: identifikacija harmonskih signalov iz točke 1,
korak: posplošitev.

Kot morebitne dodatne vire lahko tukaj priporočamo Shin and Hammond [2008] in Grant Sanderson: But what is a Fourier series? From heat flow to drawing with circles.

Zapis periodičnega signala kot vsote harmonskih signalov#

Preden podrobno spoznamo Fourierove vrste, si poglejmo definicijo splošnega harmonskega signala:

\[ x(t) = A\,\sin(\omega\,t+\varphi), \]

kjer je \(A\) amplituda, \(\omega\) krožna frekvenca (enota: rad/s) in \(\varphi\) fazni kot (enota: rad) glede na izhodišče časa. Pri tem je \(\omega=2\pi\,f\) in je \(f\) (sekundna) frekvenca (enota: 1/s = Hz). Pozitivna faza pomakne harmonsko funkcijo proti levi, negativna faza pa proti desni. Perioda \(T\) je definirana s krožno frekvenco: \(T=2\pi/\omega\).

Primer harmonskega signala z amplitudo \(A=1\), krožno frekvenco \(\omega=1\) rad/s in pozitivno fazo \(\varphi=1\) rad je prikazan spodaj.

../_images/3685991a8b852256ab4f5c5534978f131d34e728ee3bf25934437c70e6463251.png

Nadaljujmo z vsoto harmonskih signalov, pri čemer se bomo omejili na kompleksno periodične signale (glejte Klasifikacija signalov), kjer je razmerje med frekvencami posameznih harmonikov racionalno število. Frekvence harmonskih signalov bomo dodatno omejili: če je osnovna krožna frekvenca \(\omega_p=2\pi/T_p\) definirana z osnovno periodo \(T_p\), potem morajo imeti vsi ostali harmoniki krožno frekvenco, ki je večkratnik osnovne krožne frekvence.

Opisu ustreza vsota harmonskih signalov:

\[ x(t)=\frac{a_0}{2}+\sum_{n=1}^{\infty} \left[ a_n\cos\left(\frac{2\pi\,n\,t}{T_p} \right) + b_n\sin\left(\frac{2\pi\,n\,t}{T_p} \right) \right], \]

kjer je \(a_0\) konstanta, \(a_n\) amplituda \(n\)-te kosinusne komponente in \(b_n\) amplituda \(n\)-te sinusne komponente.

Spodaj si poglejmo primer harmonskega signala, ki ustreza omejitvam kompleksno periodičnega signala.

../_images/a1a38b33bf72168775dacb47f0bbab52253617e68f164a2d51e99ea8e544db34.png

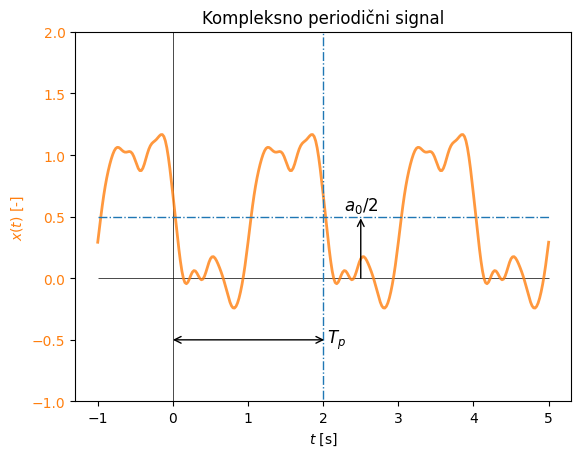
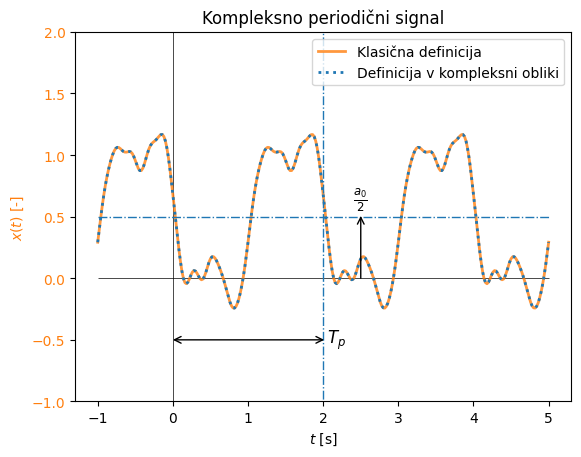
Periodični signal, ki smo si ga pogledali zgoraj, je ključnega pomena za razumevanje Fourierovih vrst (in pozneje Fourierove transformacije, glejte 3. Fourierova integralska transformacija). V nadaljevanju bomo periodični signal najprej preoblikovali v kompleksno obliko, saj nam bo to zelo poenostavilo matematični zapis in fizikalno jasnost.

Zapis v kompleksno obliko začnemo s pomočjo Eulerjeve formule:

\[ \mathrm{e}^{\pm \mathrm{i}\,\alpha} = \cos\alpha \pm \mathrm{i}\,\sin\alpha, \]

kjer je \(\mathrm{i}=\sqrt{-1}\).

Če uporabimo \(\alpha=2\pi\,n\,t/T_p\), lahko zapišemo:

\[ \cos\alpha=\frac{1}{2}\mathrm{e}^{\mathrm{i}\,\alpha}+\frac{1}{2}\mathrm{e}^{-\mathrm{i}\,\alpha} \qquad\textrm{ in } \qquad \sin\alpha=-\frac{1}{2}\,\mathrm{i}\,\mathrm{e}^{\mathrm{i}\,\alpha}+\frac{1}{2}\,\mathrm{i}\,\mathrm{e}^{-\mathrm{i}\,\alpha} \]

ter funkcijo:

\[ x(t)=\frac{a_0}{2}+\sum_{n=1}^{\infty} \left[ a_n\cos\left(\frac{2\pi\,n\,t}{T_p} \right) + b_n\sin\left(\frac{2\pi\,n\,t}{T_p} \right) \right] \]

preoblikujemo v:

\[ x(t)=\frac{a_0}{2}+\sum_{n=1}^{\infty} \left[ a_n\left( \frac{1}{2}\mathrm{e}^{\mathrm{i}\,\alpha}+\frac{1}{2}\mathrm{e}^{-\mathrm{i}\,\alpha} \right)+ b_n\left( -\frac{1}{2}\,\mathrm{i}\,\mathrm{e}^{\mathrm{i}\,\alpha}+\frac{1}{2}\,\mathrm{i}\,\mathrm{e}^{-\mathrm{i}\,\alpha} \right) \right]. \]

Urejamo naprej:

\[ x(t)=\frac{a_0}{2}+\sum_{n=1}^{\infty} \left[ \left( \frac{1}{2}a_n-\frac{1}{2}\mathrm{i}\,b_n \right)\,\mathrm{e}^{\mathrm{i}\,2\pi\,n\,t/T_p} \right] +\sum_{n=1}^{\infty} \left[ \left( \frac{1}{2}a_n+\frac{1}{2}\mathrm{i}\,b_n \right)\,\mathrm{e}^{-\mathrm{i}\,2\pi\,n\,t/T_p} \right]. \]

Zgornji izraz poenostavimo v:

\[ x(t)=\sum_{n=-\infty}^{\infty} c_n\,\mathrm{e}^{\mathrm{i}\,2\pi\,n\,t/T_p}, \]

kjer velja:

\[\begin{split} c_n = \begin{cases} \frac{1}{2}a_n-\frac{1}{2}\textrm{i}\,b_n,& \text{če } n\geq +1,\\ \frac{1}{2}a_n, & \text{če } n = 0,\\ \frac{1}{2}a_{|n|}+\frac{1}{2}\textrm{i}\,b_{|n|},& \text{če } n\leq -1.\\ \end{cases} \end{split}\]

Ugotovimo, da velja \(c_n=c_{-n}^{*}\), pri čemer smo z \({}^*\) označili kompleksno konjugirano vrednost.

Opomba

Zapis kompleksno periodičnega signala s Fourierovo vrsto z realnimi koeficienti:

\[ x(t)=\frac{a_0}{2}+\sum_{n=1}^{\infty} \left[ a_n\cos\left(\frac{2\pi\,n\,t}{T_p} \right) + b_n\sin\left(\frac{2\pi\,n\,t}{T_p} \right) \right]. \]

Opomba

Zapis kompleksno periodičnega signala s Fourierovo vrsto s kompleksnimi koeficienti:

\[ x(t)=\sum_{n=-\infty}^{\infty} c_n\,\mathrm{e}^{\mathrm{i}\,2\pi\,n\,t/T_p}. \]

Oba zapisa zgoraj seveda vodita v isti rezultat (glejte primer spodaj).

Show code cell source Hide code cell source

import numpy as np
import matplotlib.pyplot as plt


Tp = 2
t, dt = np.linspace(-0.5*Tp,2.5*Tp,301, retstep=True)
a0 = 1.
N = 10
seed = 0
rg = np.random.default_rng(seed)
a = rg.normal(size=N)*1/np.arange(1,N+1)**2 # skaliranje na koncu, da imajo višje komponente manjšo amplitudo
b = rg.normal(size=N)*1/np.arange(1,N+1)**2

c = np.zeros(2*N+1, dtype='complex')
c[N+1:] = 0.5*a-0.5j*b
c[N] = a0/2
c[:N] = np.conj(c[N+1:])[::-1]

x1 = a0/2
for n in range(N):
    x1 += a[n]*np.cos(2*np.pi*(n+1)*t/Tp) + b[n]*np.sin(2*np.pi*(n+1)*t/Tp)

x = np.zeros(len(t), 'complex')
for n in range(-N,N+1):
    x += c[N+n]*np.exp(2j*np.pi*n*t/Tp)
x = np.real(x) # teoretično pričakujemo samo realni rezultat (imaginarni del mora biti na nivoju numerične napake)
    
fig, ax1 = plt.subplots()
plt.title(f'Kompleksno periodični signal')

ax1.set_xlabel('$t$ [s]')
ax1.set_ylabel('$x(t)$ [-]', color='C1')
ax1.tick_params(axis='y', labelcolor='C1')
ax1.vlines(0, -2, 2, 'k', lw=0.5)
ax1.hlines(0, np.min(t), np.max(t), 'k', lw=0.5)
ax1.plot(t, x1, label='Klasična definicija', c='C1', lw=2, alpha=0.8) 
ax1.plot(t, x, label='Definicija v kompleksni obliki', c='C0', ls=':', lw=2, alpha=1) 
ax1.vlines([Tp], -2, 2, ls='-.', lw=1)
ax1.hlines(a0/2, np.min(t), np.max(t), ls='-.', lw=1)
ax1.annotate('$\\frac{a_0}{2}$',
            xy=(2.5, 0), xycoords='data',
            ha='center', size='large',
            xytext=(2.5, a0/2+.1), textcoords='data',
            arrowprops=dict(arrowstyle='<-',
                            connectionstyle='arc3,rad=0',
                            color="k", shrinkA=0, shrinkB=0),
            )
ax1.annotate('$T_{p}$',
            xy=(0, -0.5), xycoords='data',
            va='center', size='large', 
            xytext=(Tp+0.05, -0.5), textcoords='data',
            arrowprops=dict(arrowstyle='<->',
                            connectionstyle='arc3,rad=0',
                            color="k", shrinkA=0, shrinkB=0),
            )
ax1.legend(loc=1)
plt.ylim(-1,2)
plt.show()

../_images/840deda23de3b83c8fda90e495681255c2870102aae6b943dcf65fd2b089115b.png

Identifikacija harmonskih signalov, ki sestavljajo periodični signal#

Sedaj se lahko vrnemo na izvorno nalogo Fourierovih vrst: popis poljubnega periodičnega signala s superpozicijo različnih harmonskih signalov.

Odgovoriti moramo na vprašanje, ali v periodičnem signalu:

\[ x(t)=\sum_{n=-\infty}^{\infty} c_n\,\mathrm{e}^{\mathrm{i}\,2\pi\,n\,t/T_p},\qquad c_n=c_{-n}^* \]

lahko identificiramo harmonski signal s frekvenco \(m\)-kratnika osnovne frekvence, torej \(c_m\,\mathrm{e}^{\mathrm{i}\,2\pi\,m\,t/T_p}\)?

Izkaže se, da je to relativno enostavno; postopek začnemo z integralom periodične funkcije \(x(t)\) pomnožene z enotsko harmonsko funkcijo \(\mathrm{e}^{-\mathrm{i}\,2\pi\,m\,t/T_p}\), ki ima negativno frekvenco \(-m/T_p\) (namesto \(\textrm{i}\) imamo v eksponentu \(-\textrm{i}\)):

\[ \underbrace{\int_0^{T_p} x(t)\,\mathrm{e}^{-\mathrm{i}\,2\pi\,m\,t/T_p}\,\mathrm{d}t}_{A_m}= \underbrace{\int_0^{T_p} \sum_{n=-\infty}^{\infty} c_n\,\mathrm{e}^{\mathrm{i}\,2\pi\,n\,t/T_p} \,\,\mathrm{e}^{-\mathrm{i}\,2\pi\,m\,t/T_p}\,\mathrm{d}t}_{B_m}. \]

Ker \(x(t)\) predstavlja znani periodični signal, lahko izračunamo integral \(A_m\). \(B_m\) pa lahko poenostavimo v:

\[ B_m=\int_0^{T_p} \sum_{n=-\infty}^{\infty} c_n\,\mathrm{e}^{\mathrm{i}\,2\pi\,(n-m)\,t/T_p} \,\mathrm{d}t. \]

Zamenjajmo sedaj vrstni red seštevanja in integriranja ter izpostavimo konstanto \(c_n\):

\[ B_m= \sum_{n=-\infty}^{\infty} c_n\,\int_0^{T_p}\mathrm{e}^{\mathrm{i}\,2\pi\,(n-m)\,t/T_p} \,\mathrm{d}t. \]

Ker integriramo harmonski signal s frekvenco, ki je celi večkratnik osnovne frekvence \(1/T_p\), je rezultat vedno 0, razen takrat ko je \(n=m\):

\[\begin{split} \int_0^{T_p}\mathrm{e}^{\mathrm{i}\,2\pi\,(n-m)\,t/T_p} \,\mathrm{d}t= \begin{cases} 0,& \text{če } n\ne m,\\ T_p,& \text{če } n= m.\\ \end{cases} \end{split}\]

Sledi torej:

\[ B_m = c_m\,T_p. \]

Ker velja \(A_m=B_m\), sledi, da je neznani Fourierov koeficient \(c_m\) definiran kot (gre za kompleksno število z amplitudo in fazo):

\[ c_m = \frac{A_m}{T_p} = \frac{1}{T_p}\,\int_0^{T_p} x(t)\,\mathrm{e}^{-\mathrm{i}\,2\pi\,m\,t/T_p}\,\mathrm{d}t. \]

Ugotovili smo torej, da je posamezno harmonsko komponento relativno enostavno določiti; v praksi se pojavi težava, da dani podatki \(x(t)\) ne izpolnjujejo vseh predpostavk, predvsem ne tiste, da je harmonik celi večkratnik osnovne frekvence. S temi težavami se bomo soočili v poglavju Uporaba oken.

Posplošitev#

Fourierove vrste najpogosteje najdemo definirane v treh oblikah (\(T_p\) predstavlja osnovno periodo, \(N\) pa število harmonskih komponent, ki jih upoštevamo/identificiramo):

Fourierove vrste v eksponentni (kompleksni) obliki#

Opomba

Fourierovi koeficienti:

\[ c_n = \frac{1}{T_p}\,\int_0^{T_p} x(t)\,\mathrm{e}^{-\mathrm{i}\,2\pi\,n\,t/T_p}\,\mathrm{d}t, \]

\[ x(t)=\sum_{n=-N}^{N} c_n\,\mathrm{e}^{\mathrm{i}\,2\pi\,n\,t/T_p},\qquad c_n=c_{-n}^*. \]

Fourierove vrste v sinusno-kosinusni obliki#

Opomba

Fourierovi koeficienti:

\[ a_n = \frac{1}{T_p}\,\int_0^{T_p} x(t)\,\cos(2\pi\,n\,t/T_p)\,\mathrm{d}t, \]

\[ b_n = \frac{1}{T_p}\,\int_0^{T_p} x(t)\,\sin(2\pi\,n\,t/T_p)\,\mathrm{d}t. \]

Rekonstruirana zvezna funkcija:

\[ x(t)=\frac{a_0}{2}+\sum_{n=1}^{N} \big(a_n\,\cos(2\pi\,n\,t/T_p)+ b_n\,\sin(2\pi\,n\,t/T_p)\big). \]

Fourierove vrste v amplitudno-fazni obliki#

Opomba

Rekonstruirana zvezna funkcija:

\[ x(t)=\frac{A_0}{2}+\sum_{n=1}^{N} A_n\,\cos(2\pi\,n\,t/T_p-\varphi_n), \]

pri čemer moramo amplitudo \(A_n\) in fazo \(\varphi_n\) določiti s pomočjo eksponentne ali sinusno-kosinusne oblike in ob pomoči prehodov med posameznimi oblikami zapisov:

\[\begin{split} \begin{split} c_0 &= A_0 = a_0,\\ c_n &= \frac{A_n}{2}\,\mathrm{e}^{-\mathrm{i}\,\varphi_n} = \frac{1}{2}(a_n-\mathrm{i}\,b_n),\\ c_n &= c_{-n}^*.\\ \end{split} \end{split}\]

V tej knjigi bomo skoraj izključno uporabljali eksponentno obliko, saj je najbolj kompaktna ter enostavna za uporabo v matematičnih izpeljavah.

Nekatere lastnosti Fourierovih vrst#

Odvodi in integrali Fourierovih vrst#

Opomba

Fourierove vrste \(x(t)\) konvergirajo k danemu periodičnemu signalu \(f(t)\), če so izpolnjeni trije Dirichletovi pogoji:

signal je absolutno integrabilen: \(\int_0^{T_p}|f(x)|\mathrm{d}t < \infty\),
signal ima na območju \([0,\,T_p]\) končno število ekstremov,
signal ima na območju \([0,\,T_p]\) končno število nezveznosti.

Če signal izpolnjuje Dirichletove pogoje, Fourierova vrsta konvergira k signalu na vseh točkah območja, vključno s točkami nezveznosti. To je zelo pomemben rezultat v Fourierovi analizi, saj nam omogoča, da vsak periodični signal predstavimo kot vsoto sinusnih in kosinusnih členov.

Če Dirichletov pogoj izpolnjuje tudi odvod \(\dot{f}(t)\), potem je mogoče odvod izračunati neposredno iz Fourierovih vrst za \(x(t)\), pri čemer je treba odvajati posamezne člene.

\[ \dot{x}(t)=\sum_{n=-N}^{N} \frac{\mathrm{i}\,2\pi\,n}{T_p}\,c_n\,\mathrm{e}^{\mathrm{i}\,2\pi\,n\,t/T_p},\qquad c_n=c_{-n}^*. \]

Analogno velja za integracijo:

\[ x(t)=\sum_{n=-N}^{N} \frac{T_p}{\mathrm{i}\,2\pi\,n}\,\dot{c}_n\,\mathrm{e}^{\mathrm{i}\,2\pi\,n\,t/T_p},\qquad \dot{c}_n=\dot{c}_{-n}^*, \]

kjer so \(\dot{c}_n\) konstante Fourierove vrste za \(\dot{x}(t)\). Za primer glejte zglede v nadaljevanju.

Fourierove vrste lihih in sodih funkcij#

Funkcija \(x(t)\) je soda, če velja:

\[ x(-t)=x(t), \]

takrat velja tudi:

\[ \int_{-a}^{+a} x(t)\,\mathrm{d}t=2\,\int_0^a x(t)\,\mathrm{d}t. \]

Funkcija je liha, če velja:

\[ x(-t)=-x(t), \]

takrat velja tudi

\[ \int_{-a}^{+a} x(t)\,\mathrm{d}t=0. \]

Izpostavimo lahko, da je funkcija \(\cos()\) soda, funkcija \(\sin()\) pa liha.

Za poznejšo obravnavo je pomembna sodost/lihost produkta funkcij \(x(t)\,y(t)\). Sodost oz. lihost je odvisna od sodosti oz. lihosti funkcij \(x(t)\) in \(y(t)\).

Odnosi so definirani v tabeli spodaj.

če \(x(t)\)	če \(y(t)\)	je rezultat \(x(t)\,y(t)\)
liha	liha	soda
liha	soda	liha
soda	liha	liha
soda	soda	soda

Glede na zgornjo tabelo lahko sklenemo (glejte tudi Fourierove vrste v sinusno-kosinusni obliki):

Opomba

če iščemo Fourierovo vrsto sode periodične funkcije \(x(t)\), potem bodo sinusni členi \(b_n\) enaki nič (ker je produkt sode in lihe funkcije liha funkcija; integral lihe funkcije pa je 0).
če iščemo Fourierovo vrsto lihe periodične funkcije \(x(t)\), potem bodo kosinusni členi \(a_n\) enaki nič (ker je produkt lihe in sode funkcije liha funkcija; integral lihe funkcije pa je 0).

Nekaj zgledov#

Kompleksno periodični signal#

Najprej si bomo pogledali kompleksno periodični signal, ki smo ga spoznali in definirali že zgoraj. Signal je definiran z N = 10 harmonskimi komponentami \(c_n\), ki so v spodnjem primeru znane; tukaj bomo pokazali, da nam uporaba zgoraj definiranih enačb omogoča njihovo točno identifikacijo.

../_images/c05c5367206d8d11a43c4c4ed436788ce7b17f639821bc7cb7dcb255e6f2401d.png

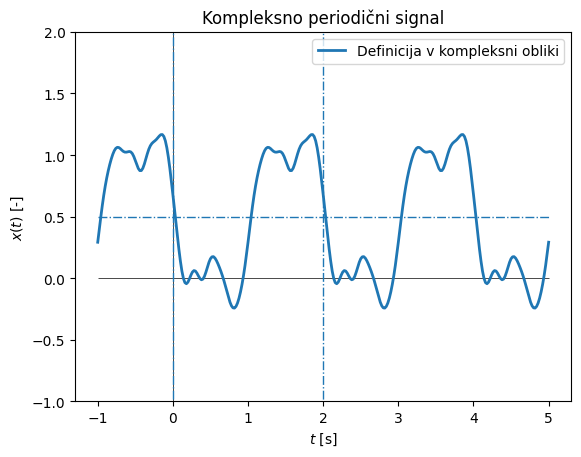
V primeru zgoraj je periodični signal generiran na podlagi vektorja Fourierovih koeficientov:

array([-0.00632711+0.00521257j, -0.00434404+0.00254093j,
        0.00739907-0.00247109j,  0.01330612-0.00555366j,
        0.00502215-0.01017038j, -0.01071339-0.02491822j,
        0.00327813-0.00683724j,  0.03557904-0.12916838j,
       -0.01651311+0.00516575j,  0.06286511-0.31163723j,
        0.5       +0.j        ,  0.06286511+0.31163723j,
       -0.01651311-0.00516575j,  0.03557904+0.12916838j,
        0.00327813+0.00683724j, -0.01071339+0.02491822j,
        0.00502215+0.01017038j,  0.01330612+0.00555366j,
        0.00739907+0.00247109j, -0.00434404-0.00254093j,
       -0.00632711-0.00521257j])

Opazimo, da je vektor kompleksno konjugiran okoli središčnega elementa. Poljubni element lahko zgolj na podlagi časovne vrste \(x(t)\) določimo tako, da sledimo definiciji:

\[ c_n = \frac{1}{T_p}\,\int_0^{T_p} x(t)\,\mathrm{e}^{-\mathrm{i}\,2\pi\,n\,t/T_p}\,\mathrm{d}t, \]

kar je v numerični implementaciji (za n = 1):

n = 1 # Poskusite še druge vrednosti, tudi n > N!
sel = np.logical_and(t>=0, t<=Tp)
np.trapz(x[sel]*np.exp(-2j*np.pi*n*t[sel]/Tp), dx=dt)/Tp

(0.06286511054669663+0.3116372312686761j)

Pri tem smo izbrali (sel) samo eno periodo v časovni vrsti. Tukaj velja poudariti, da moramo integrirati po celotni periodi. Če je napaka numerične integracije dovolj majhna (kar velja za primer zgoraj), je rezultat točen do nivoja natančnosti zapisa v računalnik.

Vredno je opozoriti, da moramo biti pri implementaciji izpeljanih izrazov zelo natančni. Hitro lahko dobimo zelo dober rezultat; vendar dokler ni točen do nivoja natančnosti zapisa v računalnik, je nekje v implementaciji napaka.

Napako bi lahko naredili, če naša diskretizacija ne bi vključevala točke pri 0 s in točke pri \(T_p\). Tako napako lahko preizkusite tako, da greste par vrstic navzgor v definicijo slike in vrstico:

t, dt = np.linspace(-0.5*Tp,2.5*Tp,301, retstep=True)

spremenite v (301 v 300):

t, dt = np.linspace(-0.5*Tp,2.5*Tp,300, retstep=True).

Odvod/integral kompleksno periodičnega signala#

Nadaljujmo z zgledom in poglejmo odvod po času. V kodi spodaj pokažemo, da je Fourierova vrsta odvoda po času res enaka Fourierovi vrsti, kjer smo vsakega od členov Fourierove vrste osnovnih podatkov preprosto odvajali.

../_images/44bc5af011c0b7cbd1ce30980b435daa7adc8d2b4b05cfb904c2996be2ee0348.png

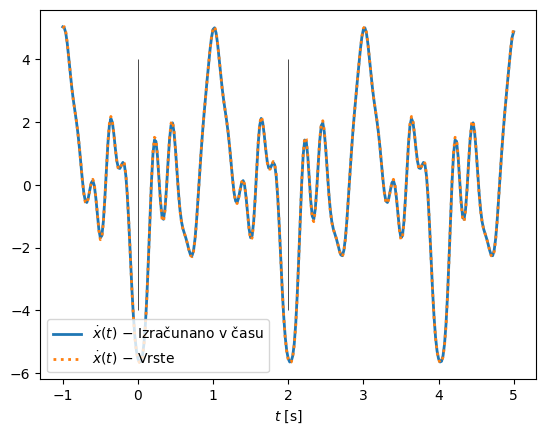
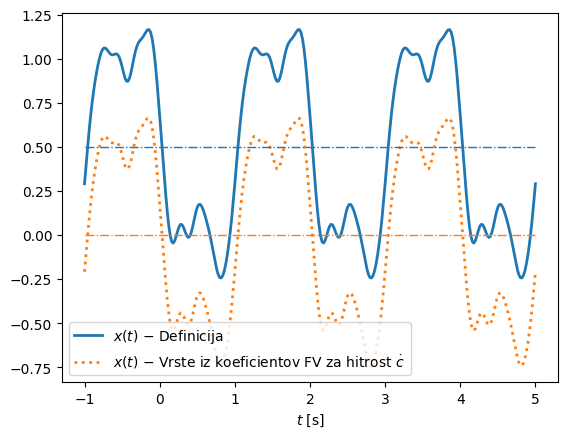
Zgornji primer lahko nadaljujemo in izvorni pomik \(x(t)\) identificiramo iz Fourierovih vrst za hitrost \(\dot x(t)\) (glejte kodo in sliko spodaj). Pri integriranju imamo težavo v primeru Fourierovega koeficienta s frekvenco 0 (statična komponenta); v kodi spodaj to frekvenco enostavno preskočimo, saj je ne moremo določiti. Podobno težavo bi imeli v času; če integriramo nedoločeni integral, potem pri integriranju potrebujemo začetno vrednost. Na sliki spodaj se zato med obema pristopoma pokaže odstopanje v velikosti statične komponente.

../_images/8b2d1f8ee3d55fdd2ed03223bb9b278bc65a4e7635fdcf3faacf4e293a002fc6.png

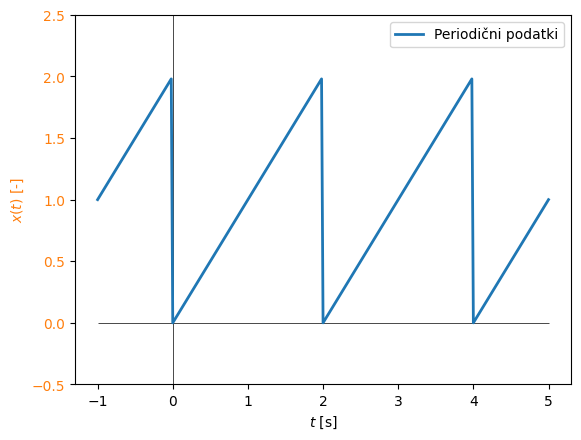
Periodični signal#

Tukaj si bomo pogledali periodični signal, ki pa s končnim številom harmonskih komponent ni kompleksno periodičen. Primer takšne funkcije je naraščajoča žaga, prikazana na spodnji sliki.

../_images/c4b0eef0288bd04b2851d7f95e8ed71f69ee5478eb7e3c28e35ff92ae38ad62e.png

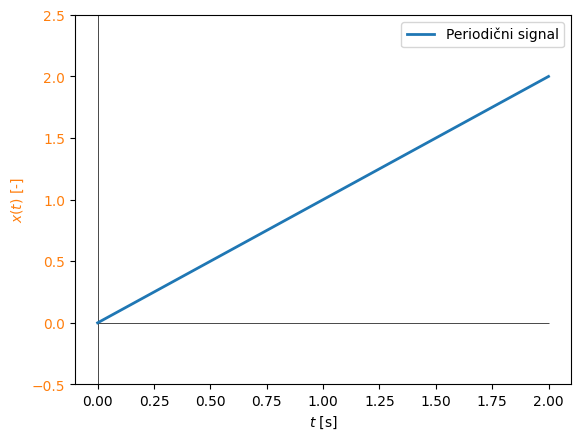
Kljub temu da signal ni kompleksno periodičen, teorija Fourierovih vrst pa je bila izpeljana ob tej predpostavki, poskusimo identificirati harmonske komponente. Najprej to naredimo na diskretni časovni vrsti. Osredotočimo se na del podatkov, ki se ponavlja:

../_images/4178f27f03fe63f0a3d46bca753aa7b28ad5a1845624bc918adccb67d185b03e.png

Identificiramo Fourierove koeficiente:

N = 10
c = np.zeros(2*N+1, dtype='complex')
n = np.arange(-N,N+1)
for i in n:
    c[i+N] = np.trapz(x*np.exp(-2j*np.pi*i*t/Tp), dx=dt)/Tp
c

array([-3.85108612e-16-0.03077684j, -3.83373888e-16-0.03442023j,
       -5.03069808e-16-0.03894743j, -2.68882139e-16-0.04473743j,
        1.52655666e-16-0.05242184j, -5.37764278e-17-0.06313752j,
       -4.16333634e-17-0.07915815j, -5.63785130e-17-0.10578895j,
       -6.24500451e-17-0.15894545j, -1.38777878e-17-0.31820516j,
        1.00000000e+00+0.j        , -1.38777878e-17+0.31820516j,
       -6.24500451e-17+0.15894545j, -5.63785130e-17+0.10578895j,
       -4.16333634e-17+0.07915815j, -5.37764278e-17+0.06313752j,
        1.52655666e-16+0.05242184j, -2.68882139e-16+0.04473743j,
       -5.03069808e-16+0.03894743j, -3.83373888e-16+0.03442023j,
       -3.85108612e-16+0.03077684j])

Na podlagi identificiranih Fourierovih koeficientov ne dobimo rezultata, ki je enak podanim podatkom (naraščajoča žaga), pač pa nov signal, ki je kompleksno periodičen:

\[ x(t)=\sum_{n=-N}^{N} c_n\,\mathrm{e}^{\mathrm{i}\,2\pi\,n\,t/T_p},\qquad c_n=c_{-n}^*. \]

Konkretna numerična koda je prikazana spodaj (pri tem smo uporabili novo numerično polje x_r, da ga ločimo od podatkov v obliki x):

x_r = np.zeros(len(t), 'complex')
for n in range(-N,N+1):
    x_r += c[N+n]*np.exp(2j*np.pi*n*t/Tp)
x_r = np.real(x_r) # teoretično pričakujemo samo realni rezultat (imaginarni del mora biti na nivoju numerične napake)

../_images/53e5969aa2bbe15c6a81363c3b4e55d56dbf5aaacbcedc8616def2307b0d622e.png

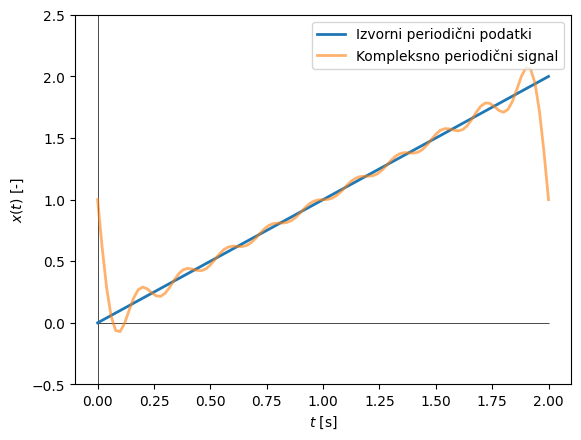
Opazimo, da identificirani kompleksno periodični signal relativno dobro opiše izvorni periodični signal. Če bi število harmonskih (\(N\)) komponent povečali, bi se identificirana funkcija izvornim podatkom bolje prilegala, vendar pa bi na mestu nezveznosti še vedno imeli odstopanje. Odstopanje na mestu nezveznosti je znano pod terminom Gibbsov fenomen. Resnici na ljubo je večina inženirskih aplikacij zveznih in zato ponavadi Gibbsov fenomen v praksi nima večjega pomena.

Analitična obravnava periodičnih signalov#

Zgoraj smo Fourierovo vrsto izračunali na diskretnih podatkih, zato smo omejeni, koliko harmonskih komponent lahko izračunamo (N < len(t)/2; zakaj je \(N\) vezan na dolžino časovne vrste, bomo spoznali pozneje). Tukaj si bomo pogledali obravnavo zveznih sistemov in Fourierovo vrsto določili s pomočjo strojnega izpeljevanja. Kot primer periodičnega signala si bomo izbrali naraščajočo žago, ki bo proporcionalna s časom t, perioda bo Tp:

import sympy as sym
sym.init_printing()

t, T_p = sym.symbols('t, T_p', real=True)
x_r = sym.fourier_series(t, limits=(t, 0, T_p))

Vrsta, sestavljena iz prvih 5 členov, je torej:

x_r.truncate(5)

../_images/6903bb8130c8e4a8a832c5b823d49a21ca841a3eedb30c353945202f95232fd5.png

Posamezen člen lahko izračunamo tudi sami:

n = 1
c_n = sym.integrate(t*sym.exp(-sym.I*2*n*sym.pi*t/T_p), (t, 0, T_p)).simplify()/T_p
c_n

../_images/227248ea6c607d36a753b842389e5f9f7119497dc9c2d1549d617473f88ce3e8.png

Da dobimo harmonsko komponento, moramo c_n pomnožiti s pripadajočo pozitivno in negativno frekvenco:

sym.simplify(c_n*sym.exp(sym.I*2*sym.pi*n*t/T_p)+sym.conjugate(c_n)*sym.exp(-sym.I*2*sym.pi*n*t/T_p))

../_images/bd35a533f083abf4be33c4b6b4adb578bc057c73fbdaec7cef86c71bdfa73447.png

Slika pri T_p = 2 in različnem številu členov v vrsti:

../_images/7e732602b589375cf5a067afbbbffe2c6a99728f50a9d095fd5bba80b1777b08.png

Diracova delta funkcija#

Diracova delta funkcija je prikazana na sliki spodaj: na celotnem definicijskem področju, razen pri vrednosti \(t=0\), ko gre proti neskončnosti, ima vrednost nič; integral Diracove delta funkcije je enak 1.

dirac-delta

Opomba

Diracova delta funkcija je definirana z:

\[ \delta(t)=0 \quad\textrm{ za } t\ne 0 \qquad\textrm{ in } \qquad \int_{-\infty}^{+\infty}\delta(t)\,\textrm{d}t=1. \]

Opomba: dejansko to ni navadna funkcija, ampak t. i. generalizirana funkcija.

Ker je integral Diracove delta funkcije 1, se včasih imenuje tudi funkcija enotskega impulza, definirana tudi kot:

\[\begin{split} \delta_{\varepsilon}= \begin{cases} \frac{1}{\varepsilon}&\textrm{ za }\quad -\frac{\varepsilon}{2}\le t\le+\frac{\varepsilon}{2},\\ 0& \textrm{sicer}. \end{cases} \end{split}\]

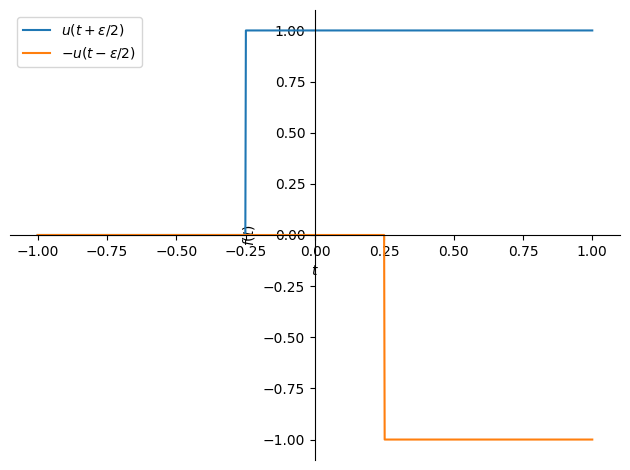
Pri definiranju enotskega impulza si lahko pomagamo tudi z dvema enotskima funkcijama stopnice. Enotska funkcija stopnice (ang. unit-step function ali tudi Heavisidova funkcija) je definirana kot:

\[\begin{split} u(t)= \begin{cases} 1&\textrm{ za }\quad t>0,\\ 0& \textrm{sicer}. \end{cases} \end{split}\]

Enotski impulz tako definiramo s pomočjo dveh funkcij enotskega koraka:

../_images/c87e86000ed6987a57a3ceb80bf1594c301154664b632673a6b859622c2e6ab4.png

Do enotskega impulza pridemo z uteženim seštevanjem:

\[ \delta_{\varepsilon}=\frac{1}{\varepsilon}\Big(u\big(t+\frac{\varepsilon}{2}\big)-u\big(t-\frac{\varepsilon}{2}\big)\Big). \]

Poglejmo si, kako koračno funkcijo pretvorimo v enotski impulz:

import sympy as sym
t, ε = sym.symbols(r't, \varepsilon')
podatki = {ε: 0.5}
unit_step = sym.Heaviside(t+ε/2) # Tukaj moramo pravilno normirati (H0), glej help!
δ_ε = 1/ε * (unit_step-unit_step.subs(ε, -ε))
δ_ε

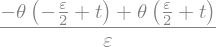
../_images/046e9a58b04143311ca0360711d62b2b177dd90bd45ca6f3840f658a257c2d5f.png

../_images/c3ec0757813b4a5e0f3fd6989d480355fbd0a81c061de66671a40f24ff38e83b.png

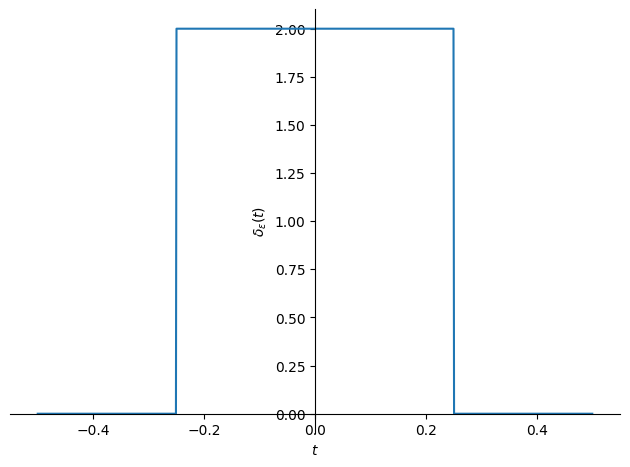
in nato integriramo (rezultat je pričakovano enak 1; spremenite \(\varepsilon\) v podatki zgoraj!):

sym.integrate(δ_ε.subs(podatki), (t, -sym.oo, sym.oo))

../_images/bcf1bef8ba4dda1c61dd817ecc62b8684dd18aec9d193bbdc4ec7e9e281c1a2d.png

Med Diracovo delta funkcijo in enotskim korakom velja tudi sledeča povezava (\(u(t)\) je koračna funkcija):

\[ \delta(t)=\lim_{\varepsilon\rightarrow 0}\delta_{\varepsilon}(t)=\frac{\textrm{d}}{\textrm{d}t}u(t). \]

Lastnosti Diracove delta funkcije#

Opomba

Je soda: \(\delta(t)=\delta(-t)\).
Sejalna lastnost \(-\) to pomeni, da integral navadne funkcije \(x(t)\) in premaknjene Diracove funkcije \(\delta(t-a)\) da vrednost funkcije \(x(a)\):\(\int_{-\infty}^{+\infty}x(t)\,\delta(t-a)\,\textrm{d}t= x(a)\).
\(\int_{-\infty}^{+\infty}\mathrm{e}^{\pm\textrm{i}\,2\pi\,a\,t}\,\textrm{d}t= \delta(a)\) ali tudi: \(\int_{-\infty}^{+\infty}\mathrm{e}^{\pm\textrm{i}\,a\,t}\,\textrm{d}t= 2\pi\,\delta(a)\), za dokaz glejte Bendat and Piersol [2011], Shin and Hammond [2008] (str. 40).
\(\delta(a\,t)=\delta(t)/|a|\).
\(\int_{-\infty}^{+\infty}f(t)\,\delta^{(n)}(t-a)\,\textrm{d}t= (-1)^n\,f^{(n)}(a)\), kjer \(n\) označuje odvod.

Padajoča žaga in njen odvod#

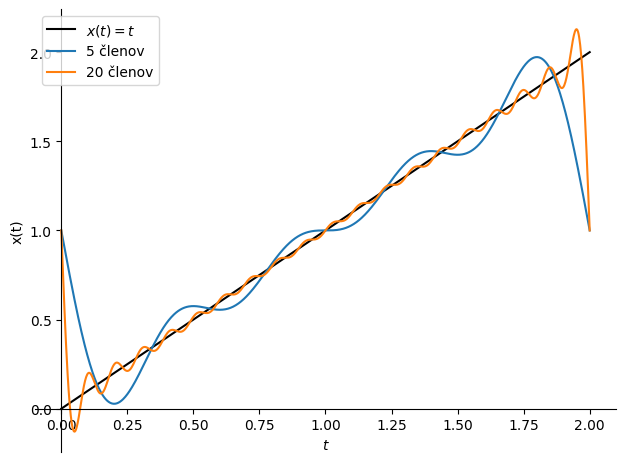
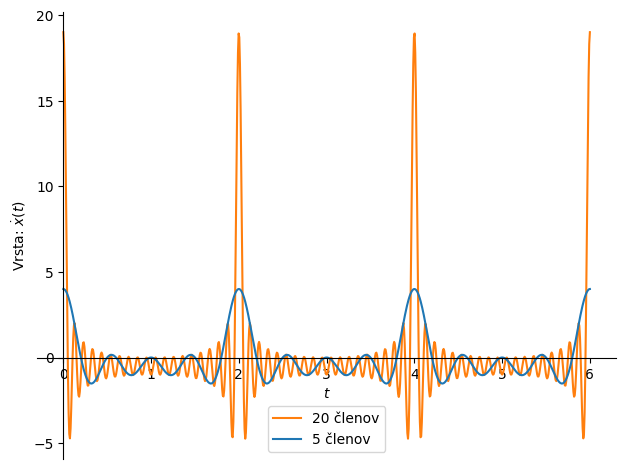
Predpostavimo periodični signal oblike padajoče žage, kot je prikazana spodaj:

../_images/dd5fc556c968e3f3b9bc03e5adf243e647b860bc18e045cd4707d87a35021350.png

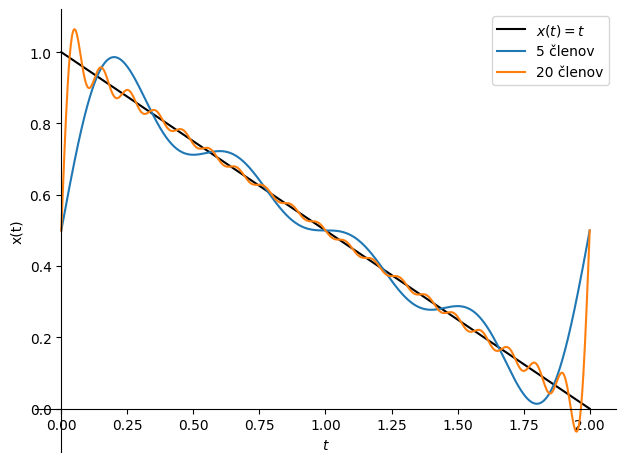
Fourierova vrsta padajočega žagastega signala je definirana kot:

\[ x(t) = \frac{1}{2}+\frac{1}{\pi}\sum_{n=1}^{\infty}\frac{1}{n}\sin\left(\frac{2\pi\,n\,t}{T_p}\right). \]

Ali s pomočjo strojnega izpeljevanja:

import sympy as sym
sym.init_printing()

t, T_p = sym.symbols('t, T_p')
podatki = {T_p: 2}
x = 1-t/T_p
x_r = sym.fourier_series(x, limits=(t, 0, T_p))

x_r.truncate(5)

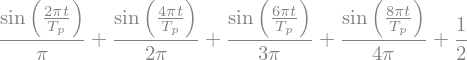
../_images/e4e2ea560ede1dfdf4afef2e8b8a1139eade1df4fd5ac432e4c1f46af52093ff.png

Če odvajamo padajočo žagasto funkcijo v času, je rezultat enak:

\[ \dot x(t) = -\frac{1}{T_p} + \sum_{n=-\infty}^{+\infty}\delta(t-n\,T_p); \]

ker pa lahko odvajamo tudi vrsto, velja tudi:

\[ \dot x(t) = \frac{2}{T_p}\sum_{n=1}^{\infty}\cos\left(\frac{2\pi\,n\,t}{T_p}\right). \]

S pomočjo zadnjih dveh enačb lahko izpeljemo izraz za vlak impulzov:

Opomba

periodični vlak impulzov (ang. train of impulses) ima v obliki Fourierovih vrst konstantne koeficiente (\(2/T_p\)):

\[ \sum_{n=-\infty}^{+\infty}\delta(t-n\,T_p) = \frac{1}{T_p} +\frac{2}{T_p}\sum_{n=1}^{\infty}\cos\left(\frac{2\pi\,n\,t}{T_p}\right). \]

To ugotovitev bomo potrebovali, ko bomo obravnavali vzorčenje signalov.

../_images/d1f296a8d6a0cc5688602c2a69e5c93c44a27369b08093e5ecfb6b52e0cbc943.png

Amplitudni in fazni spekter#

Fourierovi koeficienti \(c_n\), ki jih obravnavamo pri Fourierovih vrstah, predstavljajo amplitudno in fazno informacijo o določeni harmonski komponenti. Poglejmo si primer periodičnega pravokotnega vala na sliki spodaj:

../_images/b4aa060f21e4d77f214215c00085ea8775aba9f13cb68dbed03aba5b85bfdf6d.png

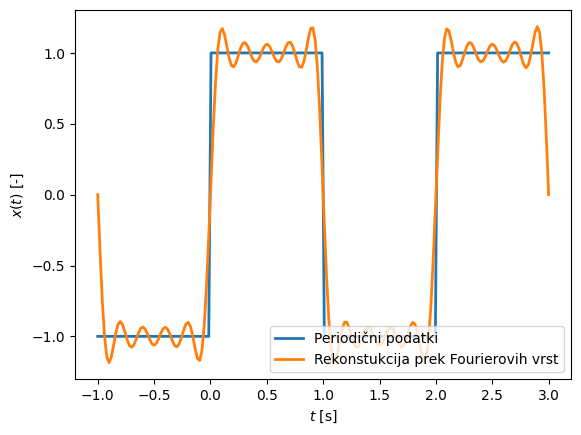
Pri pripravi podatkov zgoraj smo izračunali Fourierove koeficiente \(c\):

array([-2.77555756e-17-1.98252732e-03j, -3.12250226e-17+6.99121564e-02j,
       -1.70002901e-16-1.58622479e-03j,  3.08780779e-16+9.03023227e-02j,
        1.17961196e-16-1.18979483e-03j,  4.51028104e-17+1.26862832e-01j,
       -3.81639165e-17-7.93259458e-04j,  6.59194921e-17+2.11929286e-01j,
       -6.93889390e-18-3.96649155e-04j,  6.24500451e-17+6.36527232e-01j,
        0.00000000e+00+0.00000000e+00j,  6.24500451e-17-6.36527232e-01j,
       -6.93889390e-18+3.96649155e-04j,  6.59194921e-17-2.11929286e-01j,
       -3.81639165e-17+7.93259458e-04j,  4.51028104e-17-1.26862832e-01j,
        1.17961196e-16+1.18979483e-03j,  3.08780779e-16-9.03023227e-02j,
       -1.70002901e-16+1.58622479e-03j, -3.12250226e-17-6.99121564e-02j,
       -2.77555756e-17+1.98252732e-03j])

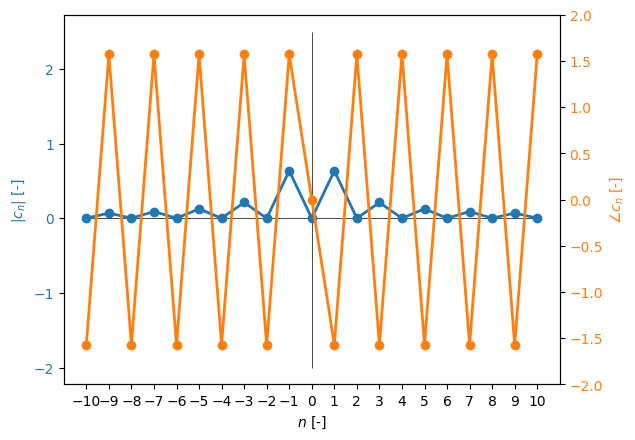
Fourierove koeficiente lahko prikažemo v grafični obliki. Če prikažemo amplitudo kompleksnega števila \(|c|\), potem govorimo o amplitudnem spektru: za določeni večkratnik osnovne frekvence \(1/T_p\) prikažemo vsebnost amplitude harmonske komponente. Podobno govorimo o faznem spektru, če prikažemo \(\angle c_n\).

../_images/6c996eef52593e9b3bdf4625a0ba34890266eb2b11e29962a4e4c7ca1d50d1fd.png

Parsevalov teorem in močnostni spekter#

Parsevalov teorem#

Če je \(x(t)\) napetost, merjena čez upor upornosti \(1\,\Omega\), potem je trenutna moč enaka \(P(t)=R\,x^2(t)\), povprečna moč periodičnega signala znotraj ene periode pa je:

\[ \frac{1}{T_p}\int_0^{T_p}x^2(t)\,\textrm{d}t; \]

ker velja \(x(t)=\sum_{n=-\infty}^{\infty}c_n\,\mathrm{e}^{\mathrm{i}\,2\pi\,n\,t/T_p}\) in \(x^2(t)=x(t)\,x^*(t)\), je povprečna moč definirana tudi kot:

\[ \frac{1}{T_p}\int_0^{T_p}x^2(t)\,\textrm{d}t= \frac{1}{T_p}\int_0^{T_p}\sum_{n=-\infty}^{\infty}c_n\,\mathrm{e}^{\mathrm{i}\,2\pi\,n\,t/T_p}\,\sum_{m=-\infty}^{\infty}c_m^*\,\mathrm{e}^{-\mathrm{i}\,2\pi\,m\,t/T_p}\,\textrm{d}t, \]

kar poenostavimo v:

\[ \frac{1}{T_p}\int_0^{T_p}x^2(t)\,\textrm{d}t= \frac{1}{T_p}\sum_{n=-\infty}^{\infty}\,\sum_{m=-\infty}^{\infty}c_n\,c_m^*\,\int_0^{T_p}\mathrm{e}^{\mathrm{i}\,2\pi\,(n-m)\,t/T_p}\,\textrm{d}t. \]

Integral harmonskega signala na zaključeni periodi je vedno nič, razen kadar je frekvenca 0. Ko je frekvenca enaka 0, je podintegralska funkcija enaka 1 in integral \(T_p\):

\[\begin{split} \int_0^{T_p}\mathrm{e}^{\mathrm{i}\,2\pi\,(n-m)\,t/T_p}\,\textrm{d}t= \begin{cases} T_p,&\textrm{če}\quad m=n,\\ 0&\textrm{sicer.}\\ \end{cases} \end{split}\]

Opomba

Sledi Parsevalov teorem ali tudi Parsevalova enakost:

\[ \frac{1}{T_p}\int_0^{T_p}x^2(t)\,\textrm{d}t= \sum_{n=-\infty}^{\infty}c_n\,c_n^*, \]

ki poveže povprečno moč v času z močjo v frekvenčni domeni.

Poglejmo si konkreten zgled:

T_p = 2
t, dt = np.linspace(0,T_p,101, retstep=True)
a0 = 1.
N = 10
seed = 0
rg = np.random.default_rng(seed)
a = rg.normal(size=N)*1/np.arange(1,N+1)**2 # skaliranje na koncu, da imajo višje komponente manjšo amplitudo
b = rg.normal(size=N)*1/np.arange(1,N+1)**2

c = np.zeros(2*N+1, dtype='complex')
c[N+1:] = 0.5*a-0.5j*b
c[N] = a0/2
c[:N] = np.conj(c[N+1:])[::-1]

x = np.zeros(len(t), 'complex')
for n in range(-N,N+1):
    x += c[N+n]*np.exp(2j*np.pi*n*t/T_p)
x = np.real(x) # teoretično pričakujemo samo realni rezultat (imaginarni del mora biti na nivoju numerične napake)

Vrednost iz časa:

np.trapz(x**2,dx=dt)/T_p

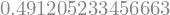
../_images/829d159c7e2d6f94c2de6ea60a87cf65e24b08cfeccc4fe51f451725ab202424.png

Vrednost na podlagi Fourierovih koeficientov:

np.dot(c,np.conjugate(c))

(0.4912052334566629+0j)

Po pričakovanjih dobimo enako vrednost (do nivoja numerične napake)!

Močnostni spekter#

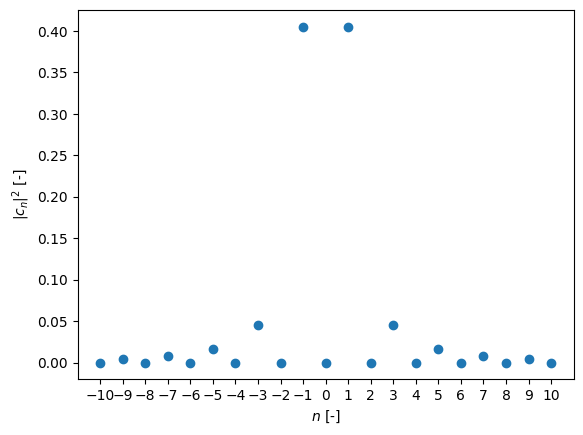
Parsevalov teorem povprečno moč definira kot vsoto kvadratov Fourierovih koeficientov oz. frekvenčnih komponent. Prikaz kvadratov posameznih frekvenčnih komponent imenujemo močnostni spekter. Pri tem je treba poudariti, da močnostni spekter izgubi informacijo o fazi in je vedno definiran z realnimi vrednostmi.

../_images/9ff66a9c6cdf18c077cf1a607549ca242611254b05c73b07d0864a90be92a814.png