5. Kvantizacija podatkov

Enakomerno časovno vzorčenje

Doslej smo obravnavali zvezne podatke \(x(t)\), pri eksperimentalnem delu pa se skoraj vedno srečamo z diskretnimi vrednostmi, ki so tipično zajete z enakomernim časovnim vzorčenjem \(x(n\,\Delta t)\), kjer je \(\Delta t\) čas (perioda) vzorčenja (\(f_s=1/\Delta t\) je frekvenca vzorčenja).

Pri razumevanju vzorčenih podatkov si pomagamo z enakomerno vzorčenimi podatki \(x_s(t)\), ki so produkt zveznih podatkov \(x(t)\) in vlaka impulzov \(i(t)\):

\[ x_s(t)=x(t)\,i(t), \]

kjer je:

\[ i(t)= \sum_{n=-\infty}^{+\infty}\delta(t-n\,\Delta t). \]

Fourierova transformacija \(x_s(t)\) je:

\[\begin{split} \begin{split} X_s(f)&=\int_{-\infty}^{+\infty} x(t)\,\sum_{n=-\infty}^{+\infty}\delta(t-n\,\Delta t)\,\mathrm{e}^{-\textrm{i}\,2\pi\,f\,t}\,\textrm{d} t\\ &=\sum_{n=-\infty}^{+\infty}\,\int_{-\infty}^{+\infty} x(t)\,\mathrm{e}^{-\textrm{i}\,2\pi\,f\,t}\,\delta(t-n\,\Delta t)\,\textrm{d} t\\ &=\sum_{n=-\infty}^{+\infty}\,x(n\,\Delta t)\,\mathrm{e}^{-\textrm{i}\,2\pi\,f\,n\,\Delta t}. \end{split} \end{split}\]

Pri prehodu v zadnjo vrstico uporabimo sejalno lastnost Diracove delta funkcije (glejte poglavje Lastnosti Diracove delta funkcije).

Ključna posledica zgornje izpeljave je: za vzorčene podatke se integral preoblikuje v vsoto vzorčenih vrednosti (pomnoženih s harmonsko modulacijo).

Ugotovimo tudi, da se Fourierova transformacija enakomerno vzorčene vrste \(X_s(f)\) ponavlja (je periodična) s frekvenco \(1/\Delta t\), kar dokažemo tako:

\[\begin{split} \begin{split} X_s(f+r/\Delta t)&=\sum_{n=-\infty}^{+\infty}\,x(n\,\Delta t)\,\mathrm{e}^{-\textrm{i}\,2\pi\,(f+r/\Delta t)\,n\,\Delta t}\\ &=\sum_{n=-\infty}^{+\infty}\,x(n\,\Delta t)\,\mathrm{e}^{-\textrm{i}\,2\pi\,f\,n\,\Delta t}\,\underbrace{\mathrm{e}^{-\textrm{i}\,2\pi\,r\,n}}_{=1}\\ &=\sum_{n=-\infty}^{+\infty}\,x(n\,\Delta t)\,\mathrm{e}^{-\textrm{i}\,2\pi\,f\,n\,\Delta t}\\ &=X_s(f), \end{split} \end{split}\]

kjer je \(r\) poljubno celo število. Sklenemo torej:

Opomba

Fourierova transformacija podatkov \(x(t)\), vzorčenih s periodo \(\Delta t\), je definirana kot vsota:

\[ X_s(f)=\sum_{n=-\infty}^{+\infty}\,x(n\,\Delta t)\,\mathrm{e}^{-\textrm{i}\,2\pi\,f\,n\,\Delta t} \]

in je v frekvenčni domeni periodična s frekvenco \(1/\Delta t\):

\[ X_s(f)=X_s(f+r/\Delta t), \qquad \textrm{kjer je:}\quad r\in \mathbb{Z}. \]

Poskusimo sedaj izpeljati inverzno Fourierovo transformacijo; najprej izraz v frekvenčni domeni pomnožimo z \(\mathrm{e}^{\textrm{i}\,2\pi\,f\,p\,\Delta t}\) (pri tem je \(p\,\Delta t\) čas, pri katerem nas zanima vrednost v času \(x(p\,\Delta t)\)) in integriramo po frekvenci \(f\):

\[ \int_{-1/(2\Delta t)}^{+1/(2\Delta t)}\,X_s(f)\,\mathrm{e}^{\textrm{i}\,2\pi\,f\,p\,\Delta t}\,\textrm{d}f=\int_{-1/(2\Delta t)}^{+1/(2\Delta t)}\,\sum_{n=-\infty}^{+\infty}\,x(n\,\Delta t)\,\mathrm{e}^{-\textrm{i}\,2\pi\,f\,n\,\Delta t}\,\mathrm{e}^{\textrm{i}\,2\pi\,f\,p\,\Delta t}\,\textrm{d}f, \]

kjer smo integrirali samo po eni periodi v frekvenci (po več ne bi bilo smiselno, saj je \(X_s(f)\) periodična funkcija).

Zgornji izraz preoblikujemo v:

\[ \sum_{n=-\infty}^{+\infty}\,x(n\,\Delta t)\,\int_{-1/(2\Delta t)}^{+1/(2\Delta t)}\,\underbrace{\mathrm{e}^{-\textrm{i}\,2\pi\,f\,(n-p)\,\Delta t}}_{=1,\textrm{ ko je } n = p;\quad\textrm{sicer je integral izraza: }0}\,\textrm{d}f=x(p\,\Delta t)\,\frac{1}{\Delta t}. \]

Opomba

Izpeljali smo torej inverzno Fourierovo transformacijo:

\[ x(p\,\Delta t) = \Delta t\,\int_{-1/(2\Delta t)}^{+1/(2\Delta t)}\,X_s(f)\,\mathrm{e}^{\textrm{i}\,2\pi\,f\,p\,\Delta t}\,\textrm{d}f. \]

Frekvenčno prekrivanje

Frekvenčno prekrivanje ali tudi frekvenčno zrcaljenje (ang. aliasing) je pojav, pri katerem pride do napačne identifikacije frekvence v signalu, razlog za to pa je neprimerno vzorčenje časovnega signala. Poglejmo detajle: vlak impulzov \(i(t)\) lahko obravnavamo kot periodične podatke s periodo \(\Delta t\) ter jih popišemo s Fourierovo vrsto:

\[ i(t)= \sum_{n=-\infty}^{+\infty}\delta(t-n\,\Delta t) = \sum_{n=-\infty}^{+\infty}c_n\,\mathrm{e}^{\textrm{i}\,2\pi\,n\,t/\Delta t}, \]

kjer je:

\[ c_n=\frac{1}{\Delta t}\,\int_{-\Delta t/2}^{+\Delta t/2}i(t)\,\mathrm{e}^{-\textrm{i}\,2\pi\,n\,t/\Delta t}\,\textrm{d}t=\frac{1}{\Delta t}. \]

Sledi:

\[ i(t)= \frac{1}{\Delta t}\, \sum_{n=-\infty}^{+\infty}\mathrm{e}^{\textrm{i}\,2\pi\,n\,t/\Delta t}. \]

Fourierova transformacija \(i(t)\), definirana s pomočjo Fourierovih vrst:

\[\begin{split} \begin{split} I(f)&= \int_{-\infty}^{+\infty}\Big(\frac{1}{\Delta t}\, \sum_{n=-\infty}^{+\infty}\mathrm{e}^{\textrm{i}\,2\pi\,n\,t/\Delta t}\Big)\, \mathrm{e}^{-\textrm{i}\,2\pi\,f\,t}\,\textrm{d}t\\ &= \frac{1}{\Delta t}\, \sum_{n=-\infty}^{+\infty}\int_{-\infty}^{+\infty} \mathrm{e}^{\textrm{i}\,2\pi\,n\,t/\Delta t}\, \mathrm{e}^{-\textrm{i}\,2\pi\,f\,t}\,\textrm{d}t\\ &= \frac{1}{\Delta t}\, \sum_{n=-\infty}^{+\infty}\int_{-\infty}^{+\infty} \mathrm{e}^{-\textrm{i}\,2\pi\,(f-n/\Delta t)\,t}\,\textrm{d}t\\ &= \frac{1}{\Delta t}\, \sum_{n=-\infty}^{+\infty} \delta\Big(f-\frac{n}{\Delta t}\Big).\\ \end{split} \end{split}\]

Zgoraj smo uporabili lastnost Diracove delta funkcije \(\int_{-\infty}^{+\infty}\mathrm{e}^{\pm\textrm{i}\,2\pi\,a\,t}\,\textrm{d}t= \delta(a)\) (glejte poglavje Lastnosti Diracove delta funkcije). Fourierova transformacija \(i(t)\) je torej v frekvenčni domeni periodično ponavljajoča se s frekvenčno periodo \(1/\Delta t\).

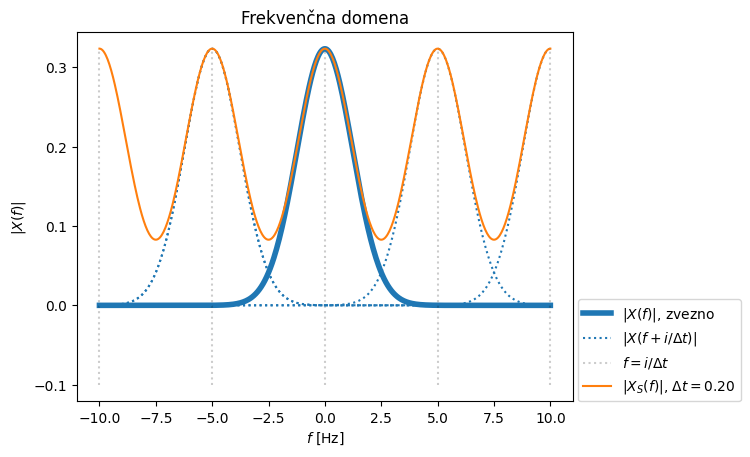
Poglejmo si sedaj povezavo \(X(f)\) in \(X_s(f)\):

\[\begin{split} \begin{split} X_s(f) =\mathcal{F}\left\{i(t)\,x(t)\right\} &= I(f)*X(f)\\ &=\int_{-\infty}^{+\infty}I(p)\,X(f-p)\,\textrm{d}p\\ &=\int_{-\infty}^{+\infty}\frac{1}{\Delta t}\, \sum_{n=-\infty}^{+\infty} \delta\Big(p-\frac{n}{\Delta t}\Big)\,X(f-p)\,\textrm{d}p\\ &=\frac{1}{\Delta t}\,\sum_{n=-\infty}^{+\infty}\,\underbrace{\int_{-\infty}^{+\infty}\, \delta\Big(p-\frac{n}{\Delta t}\Big)\,X(f-p)\,\textrm{d}p}_{\textrm{Sejalna lastnost pri $p=n/\Delta t$}}\\ &=\frac{1}{\Delta t}\,\sum_{n=-\infty}^{+\infty}\,X\Big(f-\frac{n}{\Delta t}\Big)\\ \end{split} \end{split}\]

Kako interpretiramo zgornjo izpeljavo? Če imamo časovno vzorčene podatke \(x_s(t)\), kar vodi v frekvenčni domeni do \(X_s(f)\), imamo pri določeni frekvenci \(f\) vsebnost vsote zveznih podatkov \(X(f)\) pri frekvencah \(f-n/\Delta t\), kjer gre celo število \(n\) od \(-\infty\) do \(+\infty\). V praksi to pomeni, da se nam vsebnost dejanskega (zveznega) signala iz frekvenčnega področja izven področja \([-1/(2\Delta t), +1/(2\Delta t)]\) zrcali in prekriva v frekvenčno področje od \([-1/(2\Delta t),\,+1/(2\Delta t)]\); glejte zgled spodaj.

Zgled: Gaussov impulz

Časovno vzorčenje in frekvenčno prekrivanje si bomo tukaj pogledali na primeru Gaussovega impulza/okna (glejte poglavje Gaussov impulz), ki je v časovni in frekvenčni domeni definirano kot:

\[ x(t) = \mathrm{e}^{-a\,t^2},\quad X(f)=\sqrt{\frac{\pi}{a}}\, \mathrm{e}^{-\pi^{2}\,f^{2}/a};\qquad a>0. \]

Show code cell source Hide code cell source

import sympy as sym
import matplotlib.pyplot as plt
import numpy as np

# navodilo: spreminjaj parameter `a`

t, f = sym.symbols('t, f', real=True)
n, Δt = sym.symbols('n, Δt')
a = sym.symbols('a', real=True, positive=True)
x = sym.exp(-a*t**2)
X = sym.fourier_transform(x, t, f)
Xsum = sym.Sum(X.subs(f, f-n/Δt), (n, -10, 10))

podatki = {a: 30, Δt: .2}
# pripravimo vektorizirane funkcije za numpy
f_x = sym.lambdify(t, x.subs(podatki), 'numpy')
f_X_abs = sym.lambdify(f, sym.Abs(X.subs(podatki)), 'numpy')
f_Xsum_abs = sym.lambdify(f, sym.Abs(Xsum.subs(podatki)), 'numpy')

# zaloga vrednosti v času in frekvenci (t_g so 'gosti' podatki za prikaz zvezne funkcije)
N = int(2/podatki[Δt]) # približno število -N, da imamo časovni trak cca [-2,2]
t_g = np.arange(-10*N,10*N+1)*podatki[Δt]/10
n = np.arange(-N,N+1)
t_i = n*podatki[Δt]
K = 2 # koliko sosednjih preslikav X(f) prikažemo
fr = np.linspace(-K/podatki[Δt],K/podatki[Δt], num=500)

plt.title('Časovna domena')
plt.plot(t_g, f_x(t_g), 'C0', label='$x(t)$, zvezno', linewidth=4)
plt.plot(t_i, f_x(t_i), color='C1', marker='o', ls='', label=f'$x(t_i)$, vzorčenje: $\\Delta t=${podatki[Δt]:3.2f}')
plt.xlabel('$t$ [s]')
plt.ylabel('$x(t)$')
plt.legend()
plt.show()

plt.title('Frekvenčna domena')
plt.plot(fr, f_X_abs(fr), 'C0', label='$|X(f)|$, zvezno', linewidth=4)
for i in range(-K,K):
    plt.plot(fr, f_X_abs(fr+i/podatki[Δt]), 'C0', ls=':')
    plt.vlines(i/podatki[Δt], -0.1, np.max(f_X_abs(fr)), 'k', ls=':', alpha=0.2)
plt.plot(fr, f_X_abs(fr+i/podatki[Δt]), 'C0', ls=':', label='$|X(f+i/\\Delta t)|$')
plt.vlines((i+1)/podatki[Δt], -0.1, np.max(f_X_abs(fr)), 'k', ls=':', alpha=0.2, label='$f=i/\\Delta t$')
plt.plot(fr, f_Xsum_abs(fr), color='C1', label=f'$|X_S(f)|$, $\\Delta t=${podatki[Δt]:3.2f}')
plt.xlabel('$f$ [Hz]')
plt.ylabel('$|X(f)|$')
plt.legend(loc=(1.01,0))
plt.show()

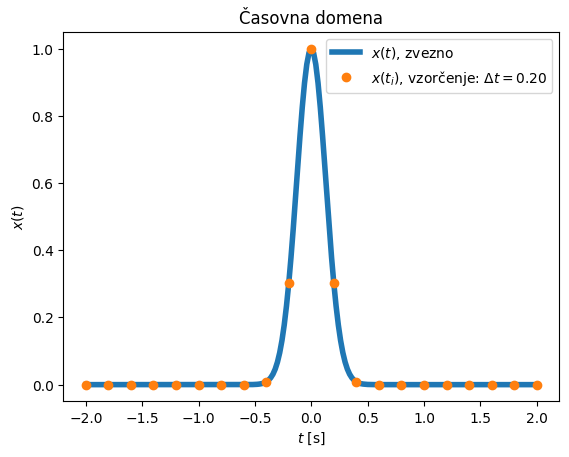
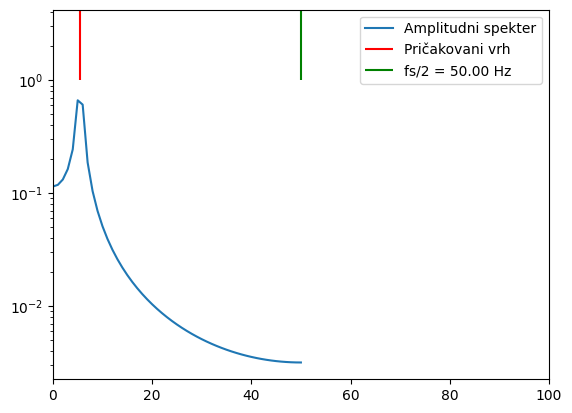
Še en primer frekvenčnega prekrivanja predstavlja spodnji zgled, kjer obravnavamo harmonske podatke. Ko je frekvenca vzorčenja fs glede na frekvenco harmonskih podatkov f prenizka (\(f>fs/2\)), se dejanska frekvenca zrcali v frekvenčno področje do fs/2. V spodnji kodi frekvenco sinusnega signala f poskusite počasi dvigovati proti (in nad) frekvenco vzorčenja fs.

Show code cell source Hide code cell source

import matplotlib.pyplot as plt
import numpy as np

f = 5.5 # <<<<<<<<<<<<<<<<
T = 1.
N = 100
t, dt = np.linspace(-T/2, T/2, N, endpoint=False, retstep=True)
fs = 1/dt
x = np.cos(2*f*np.pi*t+0.33)

X1=np.fft.rfft(x)*2/len(x)

f1=np.fft.rfftfreq(len(x),dt)
plt.semilogy(f1, np.abs(X1), label='Amplitudni spekter');
plt.vlines(f, 1, 1000, 'r', label='Pričakovani vrh')
plt.vlines(fs/2, 1, 1000, 'g', label=f'fs/2 = {fs/2:3.2f} Hz')
plt.xlim(0, fs/2+50)
plt.legend();

Preprečevanje frekvenčnega prekrivanja

Če je \(f_s=1/\Delta t\) frekvenca vzorčenja, potem se frekvenčnemu prekrivanju lahko izognemo, tako da uporabimo nizkopasovni (ang. low-pass) filter na frekvenci:

\[ f_{np}<\frac{f_s}{2}. \]

Pri tem je pomembno, da uporabimo analogni filter, preden izvedemo časovno vzorčenje. Frekvenci \(f_{np}\) rečemo tudi Nyquistova frekvenca.

Kvantizacija podatkov: pretvorba zveznih podatkov v diskretne

Za računalniško obdelavo moramo merjene zvezne podatke pretvoriti v diskretne numerične vrednosti, zajete z določeno frekvenco vzorčenja. Zajemne kartice danes omogočajo relativno hitro zajemanje (vsaj 100 kHz) pri relativno veliki dinamični globini (vsaj 24 bit). Tukaj si bomo podrobneje pogledali dinamično globino, ki predstavlja število diskretnih nivojev, na katerih zajemna kartica razpozna analogne podatke.

Zapis števil v računalniku je končne natančnosti; običajno današnji računalniki uporabljajo 64-bitno natančnost zapisa, kar je bistveno natančneje kot to omogočajo zajemne merilne kartice.

Poglejmo si naslednji zgled, kjer obravnavamo sinusoido. Če uporabimo 24-bitno kartico in tipično območje merjenja [-10, 10], je razlika med dvema nivojema kvantizacije približno 1e-6, kar je za večino meritev povsem dovolj. Razmerje med najmanjšo in največjo vrednostjo, ki jo lahko merimo na določeni zajemni kartici, imenujemo dinamični razpon ali tudi dinamična globina.

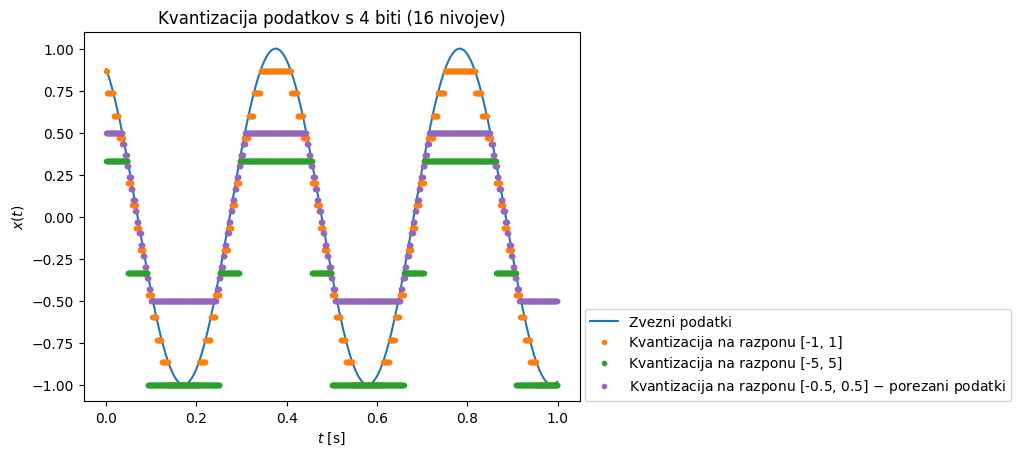
V kolikor pa uporabljamo sistem z nižjim dinamičnim razponom, pa je treba biti na območje merjenja v povezavi z dinamičnim razponom zelo pozoren in morebiti ojačati merjene podatke. Takšen primer je sinusoida spodaj, ki jo kvantiziramo na dveh območjih ([-1, 1] in [-5, 5]) s 4-bitno natančnostjo (16 nivojev).

Pri merjenju je treba paziti tudi na porezane podatke (ang. clipping), ko je območje merjenja premajhno (primer spodaj: [-0.5, 0.5]).

Opomba: koda za spodnjo sliko vključuje tudi primer, ko nam šum lahko pomaga, da izmerimo veličine, ki so manjše od nivoja kvantizacije.

Show code cell source Hide code cell source

import matplotlib.pyplot as plt
import numpy as np

T = 1
N = 1000
fr = 2.452
t, dt = np.linspace(0, T, N, endpoint=False, retstep=True)
angle = 0.5
x = 1*np.cos(2*np.pi*fr*t+angle)
# Ta primer prikaže, kako lahko naključni šum pomaga, da izmerimo nekaj kar je pod nivojem kvantizacije.
#x = 0.03*np.cos(2*np.pi*fr*t+angle)
#x = x+.2*(np.random.rand(N)-0.5)

def get_quantized(x, bits = 4, adc_range = (-2, 2)):
    x2 = x.copy()
    lo, hi = adc_range
    x2[x<=lo] = lo
    x2[x>=hi] = hi
    delta = (hi - lo) / (2**(bits)-1)
    qnt = lo+delta*np.floor((x2-lo)/delta)
    return qnt

bits = 4
levels = 2**bits
x2 = get_quantized(x, bits = bits, adc_range=(-1, 1))
x3 = get_quantized(x, bits = bits, adc_range=(-5, 5))
x4 = get_quantized(x, bits = bits, adc_range=(-.5, .5))

plt.title(f'Kvantizacija podatkov s {bits} biti ({levels} nivojev)')
plt.plot(t, x, 'C0', label='Zvezni podatki')
plt.plot(t, x2, 'C1', marker='.', linestyle='', label=f'Kvantizacija na razponu [-1, 1]')
plt.plot(t, x3, 'C2', marker='.', linestyle='', label=f'Kvantizacija na razponu [-5, 5]')
plt.plot(t, x4, 'C4', marker='.', linestyle='', label=f'Kvantizacija na razponu [-0.5, 0.5] $-$ porezani podatki')
plt.xlabel('$t$ [s]')
plt.ylabel('$x(t)$')
plt.legend(loc=(1.01,0))
plt.show()

Razmerje med signalom in šumom

Razliko med kvantizirano in dejansko vrednostjo lahko obravnavamo kot naključni šum \(e\) z enakomerno porazdelitvijo znotraj koraka kvantizacije. Standardna deviacija takega šuma je definirana kot (Shin and Hammond [2008], str.: 133):

\[ \sigma_e=\frac{A/2^b}{\sqrt{12}}, \]

kjer je \(A\) celotni razpon območja kvantizacije in \(b\) število bitov kvantizacije, brez bita za predznak. Pri 24-bitni kvantizaciji na območju od -10 do 10 (\(A=20\)) je standardna deviacija šuma:

\[ \sigma_e = \frac{20/2^{23}}{\sqrt{12}}=6.88\cdot 10^{-7}. \]

Pri vrednotenju deleža koristnih informacij proti šumu si pomagamo z:

Opomba

razmerjem med signalom in šumom (ang. signal-to-noise ratio):

\[ \textrm{SNR}=10\log_{10}\Big(\frac{\sigma_x^2}{\sigma_e^2}\Big), \]

kjer \(\sigma_x^2\) in \(\sigma_e^2\) predstavljata moč koristnih informacij (signal \(x\)) in šuma (\(e\)).

Če predpostavimo, da je \(\sigma_x=A/4\) (da preprečimo rezanje podatkov), izpeljemo:

\[ \textrm{SNR}=10\log_{10}\Big(\frac{(A/4)^2}{\big(\frac{A/2^b}{\sqrt{12}}\big)^2}\Big)= 10\log_{10}\big(3/4\cdot 2^{2b}\big)\approx -1.25+6\,b\,\textrm{dB}. \]

V primeru 12-bitne kvantizacije je \(b=11\) in imamo na voljo približno 65 dB dinamičnega razpona, v primeru 24-bitne kvantizacije pa bi bil teoretično razpon približno 137 dB. V praksi imamo opravka še z drugimi viri šuma, ki povzročijo, da so vrednosti SNR bistveno nižje. Spodaj je prikazan idealiziran primer šuma in podatkov, ki niso obremenjeni s šumom.

Show code cell source Hide code cell source

import sympy as sym
import matplotlib.pyplot as plt
import numpy as np

T = 1.5
N = 1000
w = 0.5
t = np.linspace(-T/2, T/2, N, endpoint=False)
dt = t[1] - t[0]
x = np.cos(2*np.pi*t/(2*w*T))
x[np.logical_or(-w*T*0.5 > t , t > w*T*0.5)] = 0.
n = 0.1*(np.random.rand(N)-0.5)

plt.title(f'Prikaz podatkov s SNR = {10*np.log10(np.std(x)**2/np.std(n)**2):3.2f} dB')
plt.plot(t, n, label='Šum')
plt.plot(t, x+n, label='Signal + šum')
plt.plot(t, x, label='Signal')
plt.xlabel('$t$ [s]')
plt.legend()
plt.show()