3. Fourierova integralska transformacija#
Če so Fourierove vrste omejene na periodične podatke, je pri Fourierovi integralski transformaciji cilj posplošitev na neperiodične podatke. Ideja je, da to dosežemo tako, da periodo \(T_p\) razširimo v neskončnost. V nadaljevanju si bomo pogledali detajle.
Izračun Fourierove vrste (2. Fourierove vrste) temelji na periodi \(T_p\); integral za izračun koeficientov lahko definiramo od \(-T_p/2\) do \(+T_p/2\):
kjer je \(\omega_p=2\pi/T_p\) osnovna krožna frekvenca. Kadar \(T_p\) postane velik in gre proti neskončnosti \(T_p\rightarrow \infty\), gre osnovna krožna frekvenca proti nič: \(\omega_p\rightarrow 0\). Da se izognemo težavam pri deljenju z \(\infty\), pomnožimo zgornji izraz s \(T_p\), uporabimo \(\omega_n=n\,\omega_p\) in nadaljujemo:
Ob predpostavki da limita obstaja, zapišemo Fourierovo transformacijo (tudi Fourierov integral):
kjer smo namesto \(\omega_{n}\) zapisali \(\omega\), saj je sedaj frekvenca zvezno definirana. \(X(\omega)\) predstavlja amplitudno frekvenčno gostoto, saj je \(c_n\,T_p=c_n/\Delta f\), pri čemer je \(\Delta f\) frekvenčna pasovna širina (ang. bandwidth). S \(\mathcal{F}\{\}\) označimo Fourierovo transformacijo.
Poglejmo si sedaj še rekonstruirano zvezno funkcijo, kadar gre \(T_p\rightarrow \infty\):
Navedeni izraz je zvezen in ga imenujemo inverzna Fourierova transformacija. Označimo ga s \(\mathcal{F}^{-1}\{\}\):
V izrazu zgoraj smo uporabili \(\textrm{d}f=\textrm{d}\omega/(2\pi)\).
Opomba
Tukaj še enkrat ponovimo Fourierovo transformacijo in njeno inverzno obliko, zapisano v krožni frekvenci:
Opomba
V numeričnih metodah pa je frekvenca pogosteje definirana v sekundni frekvenci, takrat sta Fourierova transformacija in njena inverzna oblika definirani kot:
Nekaj primerov Fourierove transformacije#
Diracova delta funkcija#
Najprej si poglejmo Fourierovo transformacijo Diracove delta funkcije \(\delta(t)\):
Na podlagi zgornje izpeljave zaključimo, da je Diracova delta funkcija v času neskončno kratka, v frekvenčni domeni pa neskončno široka (zasede celotni spekter oz. vse frekvence). Veljalo bi tudi obratno: če bi delta funkcijo definirali v frekvenčni domeni, bi bila neskončno ozka, v času pa neskončno široka. K temu konceptu se bomo pozneje vračali.
Simetrična eksponentno padajoča funkcija#
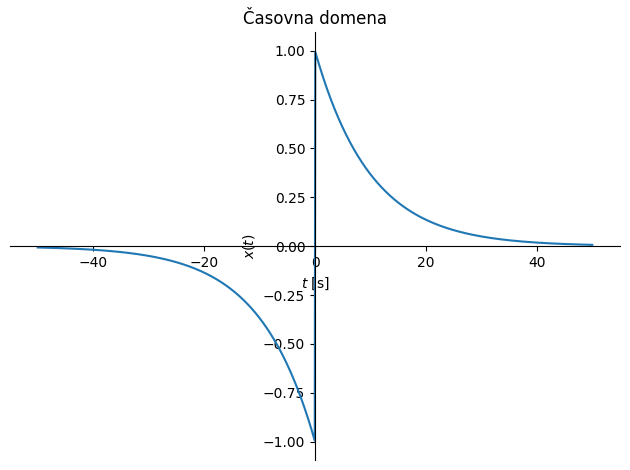
Poglejmo si sedaj še simetrično eksponentno padajočo funkcijo \(x(t)\):
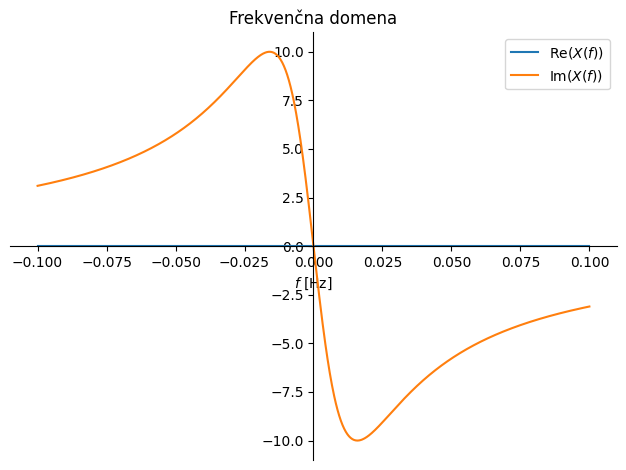
Fourierova transformacija:
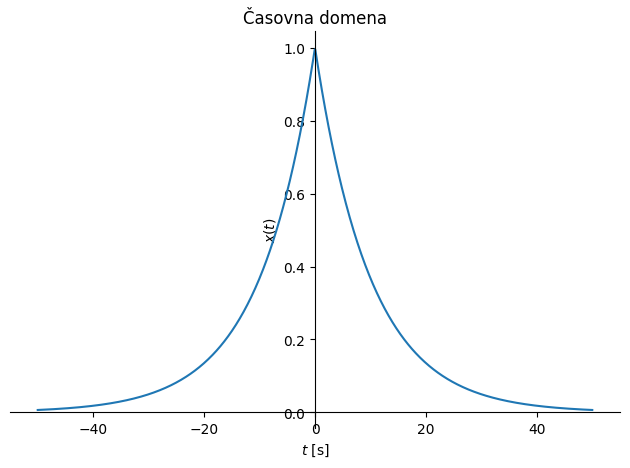
Opazimo, da je pri frekvenci 0 Hz amplituda \(X(0)=2/\eta\) in pri frekvenci \(f_{1/2}=|\eta/(2\pi)|\) pade na polovico začetne amplitude. Parameter \(\eta\) definira časovni raztros; večja kot je vrednost \(\eta\), hitreje bo funkcija konvergirala k vrednosti nič v časovni domeni in počasneje v frekvenčni domeni. Podobno kot pri delta funkciji torej ugotovimo, da majhen časovni raztros rezultira v velik frekvenčni raztros in obratno.
Poglejmo si sedaj zgled v času in frekvenci:
Show code cell source
import sympy as sym
t, f = sym.symbols('t, f', real=True)
η = sym.symbols('\\eta', real=True, positive=True)
podatki = {η: 0.1}
x = sym.exp(-η*sym.Abs(t))
X = sym.fourier_transform(x, t, f)
sym.plot(x.subs(podatki), (t,-50,50), xlabel='$t$ [s]', ylabel='$x(t)$', title='Časovna domena')
p1 = sym.plot(sym.re(X.subs(podatki)), (f,-.1,.1), xlabel='$f$ [Hz]', label='Re$(X(f))$', ylabel='', title='Frekvenčna domena', show=False)
p2 = sym.plot(sym.im(X.subs(podatki)), (f,-.1,.1), line_color='C1', label='Im$(X(f))$', show=False)
p1.extend(p2)
p1.legend = True
p1.show()
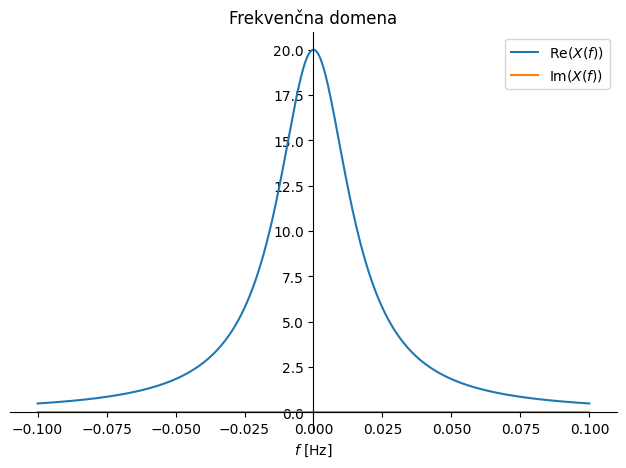
Pri primeru zgoraj opazimo, da simetrična eksponentna funkcija rezultira v Fourierovo transformacijo, ki ima samo realno komponento različno od nič. To sicer velja za vse sode funkcije; za lihe funkcije bi veljalo obratno: neničelna bi bila imaginarna komponenta (slika spodaj). Podobno smo sicer ugotovili že pri Fourierovih vrstah sodih in lihih funkcij (za več glejte Fourierove vrste lihih in sodih funkcij).
Show code cell source
import sympy as sym
t, f = sym.symbols('t, f', real=True)
η = sym.symbols('\\eta', real=True, positive=True)
podatki = {η: 0.1}
x = sym.sign(t)*sym.exp(-η*sym.Abs(t))
X = sym.fourier_transform(x, t, f)
sym.plot(x.subs(podatki), (t,-50,50), xlabel='$t$ [s]', ylabel='$x(t)$', title='Časovna domena')
p1 = sym.plot(sym.re(X.subs(podatki)), (f,-.1,.1), xlabel='$f$ [Hz]', label='Re$(X(f))$', ylabel='',
title='Frekvenčna domena', show=False)
p2 = sym.plot(sym.im(X.subs(podatki)), (f,-.1,.1), line_color='C1', label='Im$(X(f))$', show=False)
p1.extend(p2)
p1.legend = True
p1.show()
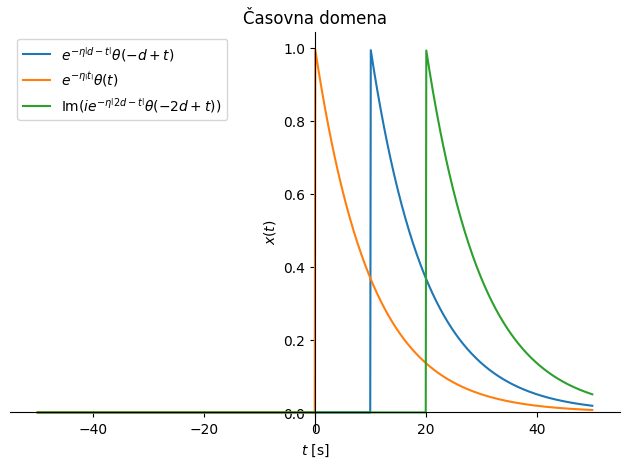
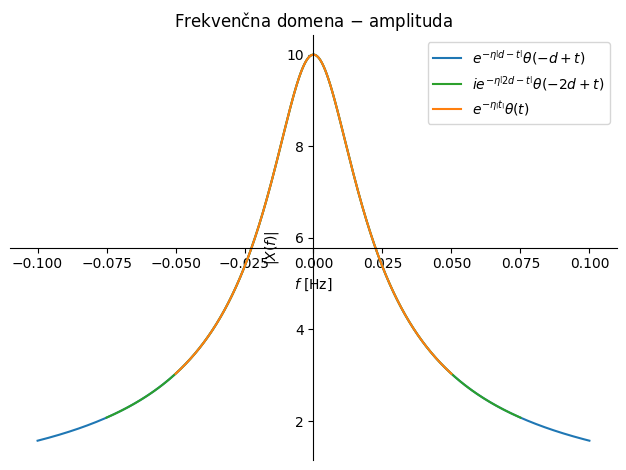
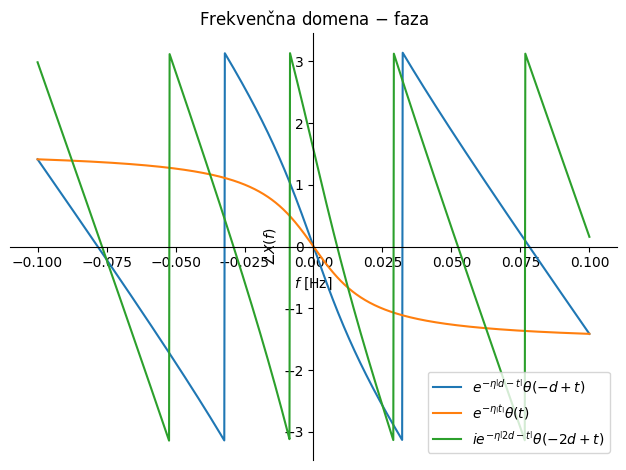
Sicer pa velja poudariti, da v splošnem realni signali \(x(t)\) po Fourierovi transformaciji postanejo kompleksni, njihova amplituda je soda, faza pa liha funkcija (slika spodaj; \(\theta(t)\) označuje enotsko funkcijo stopnice). Časovni signali so v splošnem lahko kompleksne oblike in takrat v frekvenčni domeni v splošnem ne opazimo sodosti/lihosti amplitude ali faze (poskusite spremeniti kodo spodaj).
Show code cell source
import sympy as sym
t, f, d = sym.symbols('t, f, d', real=True)
η = sym.symbols('\\eta', real=True, positive=True)
podatki = {η: 0.1, d: 10}
x = sym.Heaviside(t-d)*sym.exp(-η*sym.Abs(t-d))
# x = sym.sign(t-d)*sym.exp(-η*sym.Abs(t-d)) # časovni zamik, liha funkcija, povprečje nič
x2 = sym.Heaviside(t)*sym.exp(-η*sym.Abs(t))
x3 = sym.I*sym.Heaviside(t-2*d)*sym.exp(-η*sym.Abs(t-2*d)) # kompleksna časovna vrsta; to bo hitro
# x3 = sym.I*sym.sign(t-2*d)*sym.exp(-η*sym.Abs(t-2*d)) # kompleksna časovna vrsta; to bo hitro, liha funkcija, povprečje nič
# x = x + sym.I*sym.sign(t)*sym.exp(-η*sym.Abs(t)) # kompleksna časovna vrsta; to bo trajalo
X = sym.fourier_transform(x, t, f)
X2 = sym.fourier_transform(x2, t, f)
X3 = sym.fourier_transform(x3, t, f)
p1 = sym.plot(x.subs(podatki), (t,-50,50), xlabel='$t$ [s]', ylabel='$x(t)$',
line_color='C0', title='Časovna domena', show=False, label=f'${sym.latex(x)}$')
p2 = sym.plot(x2.subs(podatki), (t,-50,50), line_color='C1', label=f'${sym.latex(x2)}$', show=False)
p3 = sym.plot(sym.im(x3).subs(podatki), (t,-50,50), line_color='C2', label=f'Im(${sym.latex(x3)}$)', show=False)
p1.extend(p2)
p1.extend(p3)
p1.legend = True
p1.show()
p1 = sym.plot(sym.Abs(X.subs(podatki)), (f,-.1,.1), line_color='C0', xlabel='$f$ [Hz]', ylabel='$|X(f)|$',
title='Frekvenčna domena $-$ amplituda', show=False, label=f'${sym.latex(x)}$')
p2 = sym.plot(sym.Abs(X2.subs(podatki)), (f,-.05,.05), line_color='C1', label=f'${sym.latex(x2)}$', show=False)
p3 = sym.plot(sym.Abs(X3.subs(podatki)), (f,-.075,.075), line_color='C2', label=f'${sym.latex(x3)}$', show=False)
p1.extend(p3)
p1.extend(p2)
p1.legend = True
p1.show()
p1 = sym.plot(sym.arg(X.subs(podatki)), (f,-.1,.1), line_color='C0', xlabel='$f$ [Hz]', ylabel='$\\angle X(f)$',
title='Frekvenčna domena $-$ faza', show=False, label=f'${sym.latex(x)}$')
p2 = sym.plot(sym.arg(X2.subs(podatki)), (f,-.1,.1), line_color='C1', label=f'${sym.latex(x2)}$', show=False)
p3 = sym.plot(sym.arg(X3.subs(podatki)), (f,-.1,.1), line_color='C2', label=f'${sym.latex(x3)}$', show=False)
p1.extend(p2)
p1.extend(p3)
p1.legend = True
p1.show()
Sinusna funkcija#
Predpostavimo sinusno funkcijo:
ki jo preoblikujemo v:
in potem nadaljujemo z izračunom Fourierove transformacije:
import sympy as sym
A, t, f = sym.symbols('A, t, f', real=True)
p = sym.symbols('p', real=True, positive=True)
i = sym.I
π = sym.pi
x = A*(sym.exp(i*2*π*p*t)-sym.exp(-i*2*π*p*t))/(2*i)
X = sym.fourier_transform(x, t, f)
X
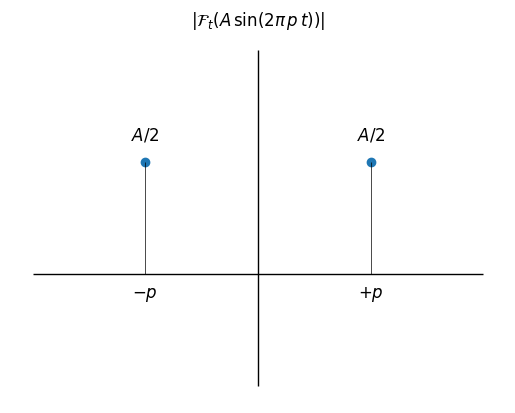
V zgornji strojni izpeljavi \(\mathcal{F}_{t}[\cdot]\) predstavlja Fourierovo transformacijo. Glede na lastnosti Diracove delta funkcije (glejte Lastnosti Diracove delta funkcije) vemo, da velja \(\mathcal{F}_{t}\left[\mathrm{e}^{-2\,\textrm{i}\,\pi\,p\,t}\right]\left(f\right)=\delta(p+f)\), iz česar sledi:
kar prikažemo na sliki spodaj.
Show code cell source
import numpy as np
import matplotlib.pyplot as plt
A = 1
p = 10
fig, ax1 = plt.subplots()
plt.title('$|\\mathcal{F}_{t}\\left( A\\,\\sin(2\\pi\\,p\\,t)\\right)|$')
ax1.set_xlabel('$f$')
ax1.set_ylabel('$|\\mathcal{F}()|$')
ax1.plot([-p, p], [A/2, A/2], 'o')
ax1.vlines(0, -0.5*A, A, 'k', lw=1)
ax1.vlines(-p, 0, A/2, 'k', lw=0.5)
ax1.vlines(p, 0, A/2, 'k', lw=0.5)
ax1.hlines(0, -2*p, 2*p, 'k', lw=1)
ax1.annotate('$-p$',
xy=(-p, -0.5), xycoords='data',
ha='center', size='large',
xytext=(-p, -0.1), textcoords='data'
)
ax1.annotate('$+p$',
xy=(p, -0.5), xycoords='data',
ha='center', size='large',
xytext=(p, -0.1), textcoords='data'
)
ax1.annotate('$A/2$',
xy=(-p, A/2), xycoords='data',
ha='center', size='large',
xytext=(-p, A/2+.1), textcoords='data'
)
ax1.annotate('$A/2$',
xy=(p, A/2), xycoords='data',
ha='center', size='large',
xytext=(p, A/2+.1), textcoords='data'
)
plt.axis('off')
plt.show()
Pravokotni impulz#
Predpostavimo pravokotno funkcijo:
kar v primeru Fourierove transformacije vodi v izraz:
ki ga lahko preoblikujemo v:
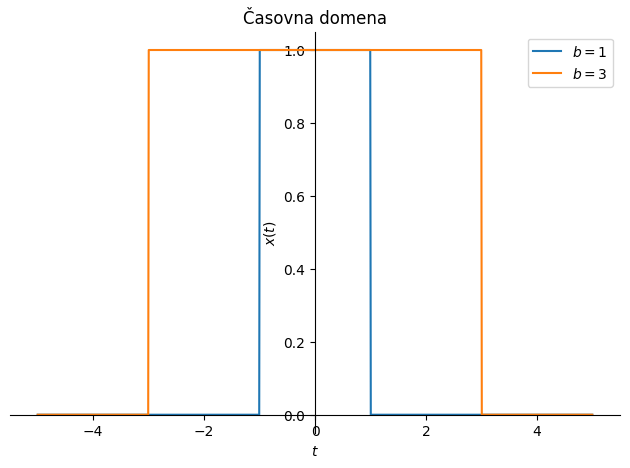
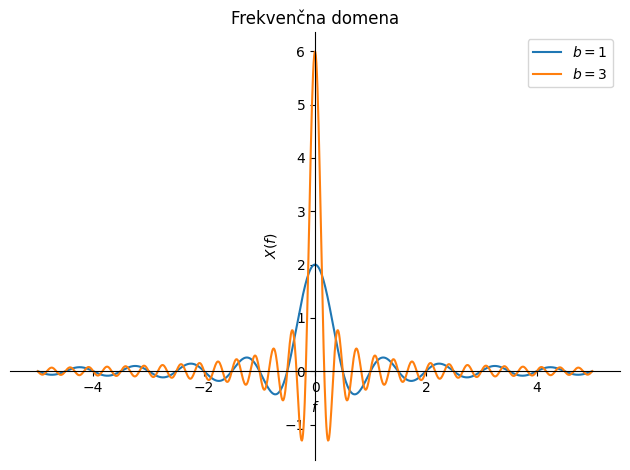
Zgornji izraz jasno kaže: ko \(f\) limitira proti 0, \(X(f)\) limitira k \(2\,a\,b\); sicer pa v frekvenčni domeni oscilira s frekvenco \(1/b\). Nekatere karakteristike vidimo iz slike spodaj: ponovno opazimo, da širši kot so podatki v času, ožji so v frekvenci.
Show code cell source
import sympy as sym
a, b, f = sym.symbols('a, b, f', real=True, positive=True)
t = sym.symbols('t', real=True)
i = sym.I
π = sym.pi
x = a*sym.Heaviside(t+b) - a*sym.Heaviside(t-b)
X = sym.simplify(sym.integrate(a*sym.exp(-i*2*π*f*t), (t, -b, b)), trig=True)
podatki = {a: 1, b:1}
podatki2 = {a: 1, b:3}
p1 = sym.plot(x.subs(podatki), (t, -5, +5), line_color='C0', label=f'$b={b.subs(podatki)}$',show=False,
title='Časovna domena', ylabel='$x(t)$', xlabel='$t$')
p2 = sym.plot(x.subs(podatki2), (t, -5, +5), line_color='C1', label=f'$b={b.subs(podatki2)}$',show=False)
p1.extend(p2)
p1.legend = True
p1.show()
p1 = sym.plot(X.subs(podatki), (f, -5, +5), line_color='C0', label=f'$b={b.subs(podatki)}$',show=False,
title='Frekvenčna domena', ylabel='$X(f)$', xlabel='$f$')
p2 = sym.plot(X.subs(podatki2), (f, -5, +5), line_color='C1', label=f'$b={b.subs(podatki2)}$',show=False)
p1.extend(p2)
p1.legend = True
p1.show()
Dušeni odziv#
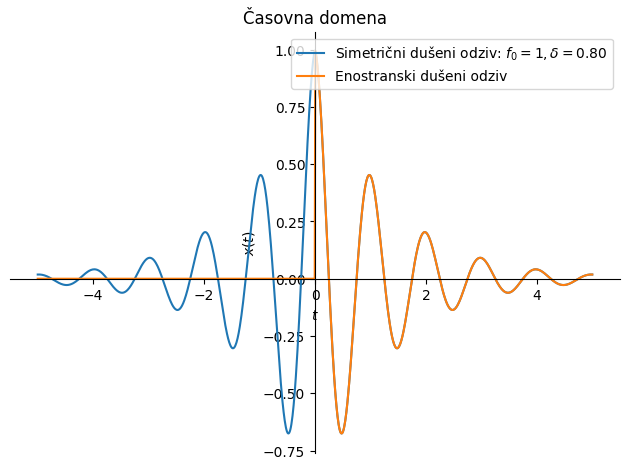
Tukaj si bomo najprej pogledali simetrični dušeni odziv:
in nato še enostranski dušeni odziv:
Fourierovo transformacijo za oba dušena odziva izpeljemo (in nato prikažemo):
import sympy as sym
t, f = sym.symbols('t, f', real=True)
δ = sym.symbols('\\delta', real=True, positive=True)
f_0 = sym.symbols('f_0', real=True, positive=True)
i = sym.I
π = sym.pi
podatki = {δ: 0.1, f_0: 1}
x_1 = sym.exp(-δ*sym.Abs(t))*sym.cos(2*π*f_0*t)
x_2 = sym.Heaviside(t)*sym.exp(-δ*t)*sym.cos(2*π*f_0*t)
X_1 = sym.fourier_transform(x_1, t, f)
X_2 = sym.fourier_transform(x_2, t, f)
X_2
Show code cell source
import sympy as sym
t, f = sym.symbols('t, f', real=True)
δ, f_0 = sym.symbols('\\delta, f_0', real=True, positive=True)
i = sym.I
π = sym.pi
podatki = {δ: 0.1, f_0: 1}
x_1 = sym.exp(-δ*sym.Abs(t))*sym.cos(2*π*f_0*t)
x_2 = sym.Heaviside(t)*sym.exp(-δ*t)*sym.cos(2*π*f_0*t)
X_1 = sym.fourier_transform(x_1, t, f)
X_2 = sym.fourier_transform(x_2, t, f)
podatki = {f_0: 1, δ:0.8}
p1 = sym.plot(x_1.subs(podatki), (t, -5, +5), line_color='C0',
label=f'Simetrični dušeni odziv: $f_0={f_0.subs(podatki)}, \\delta={δ.subs(podatki):3.2f}$', show=False,
title='Časovna domena', ylabel='$x(t)$', xlabel='$t$')
p2 = sym.plot(x_2.subs(podatki), (t, -5, +5), line_color='C1', label='Enostranski dušeni odziv',show=False)
p1.extend(p2)
p1.legend = True
p1.show()
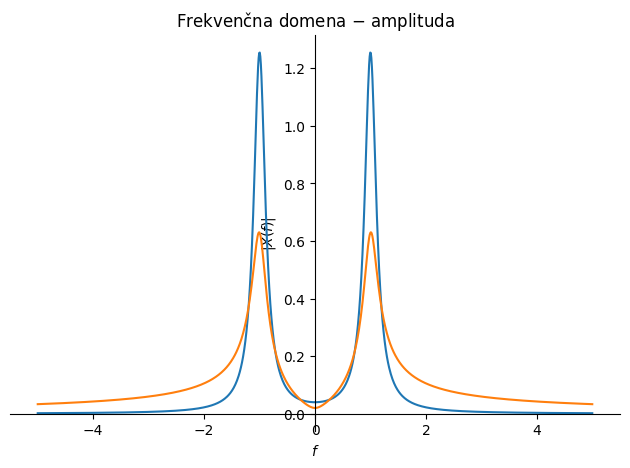
p1 = sym.plot(sym.Abs(X_1).subs(podatki), (f, -5, +5), line_color='C0', show=False,
title='Frekvenčna domena $-$ amplituda', ylabel='$|X(f)|$', xlabel='$f$')
p2 = sym.plot(sym.Abs(X_2).subs(podatki), (f, -5, +5), line_color='C1', show=False)
p1.extend(p2)
p1.show()
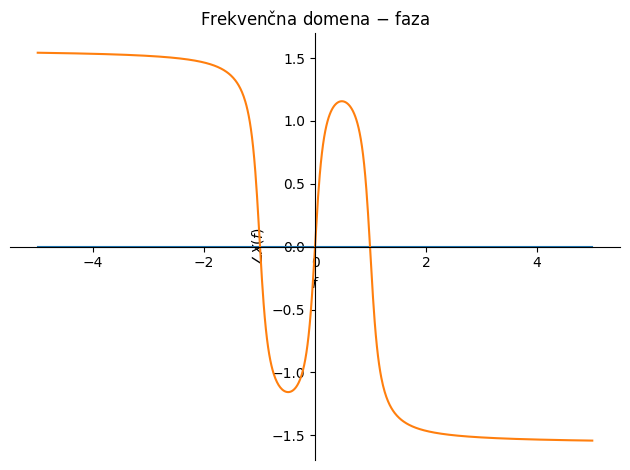
p1 = sym.plot(sym.arg(X_1).subs(podatki), (f, -5, +5), line_color='C0', show=False,
title='Frekvenčna domena $-$ faza', ylabel='$\\angle X(f)$', xlabel='$f$')
p2 = sym.plot(sym.arg(X_2).subs(podatki), (f, -5, +5), line_color='C1', show=False)
p1.extend(p2)
p1.show()
Gaussov impulz#
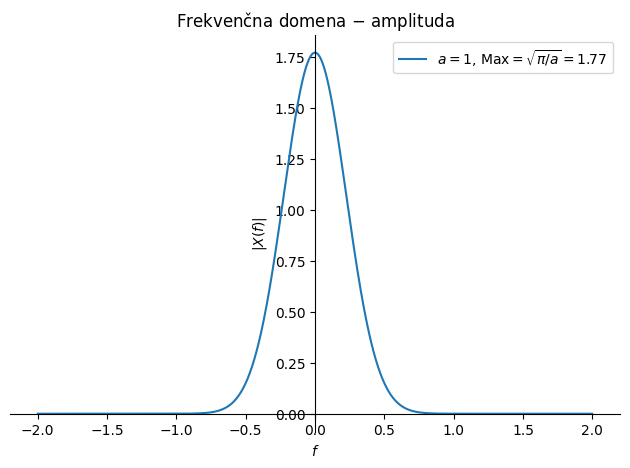
Gaussovo okno ima zelo pomembno mesto pri različnih teoretičnih izpeljavah (npr. porazdelitev verjetnosti, okna, valčna transformacija) in zato si bomo tukaj pogledali njegovo obliko v frekvenčni domeni. Najprej definirajmo:
Fourierovo transformacijo izpeljemo (spodaj), pri čemer rezultira v:
import sympy as sym
t, f = sym.symbols('t, f', real=True)
a = sym.symbols('a', real=True, positive=True)
x = sym.exp(-a*t**2)
X = sym.fourier_transform(x, t, f)
X
Rezultat nato še grafično prikažemo (ker je Gaussova funkcija soda, je faza v frekvenčni domeni enaka 0):
Show code cell source
import sympy as sym
t, f = sym.symbols('t, f', real=True)
a = sym.symbols('a', real=True, positive=True)
x = sym.exp(-a*t**2)
X = sym.fourier_transform(x, t, f)
podatki = {a: 1}
p1 = sym.plot(x.subs(podatki), (t, -2, +2), line_color='C0',
label=f'$a={a.subs(podatki)}$', show=False,
title='Časovna domena', ylabel='$x(t)$', xlabel='$t$')
p1.legend = True
p1.show()
p1 = sym.plot(sym.Abs(X).subs(podatki), (f, -2, +2), line_color='C0',
label=f'$a={a.subs(podatki)}$'+', Max$=\\sqrt{\\pi/a}=$'+f'{sym.sqrt(sym.pi/a).evalf(subs=podatki):3.2f}', show=False,
title='Frekvenčna domena $-$ amplituda', ylabel='$|X(f)|$', xlabel='$f$')
p1.legend = True
p1.show()

Lastnosti Fourierove transformacije#
Linearnost (ang. linearity)#
Opomba
Fourierova transformacija je linearna, kar pomeni:
Še izpeljava:
import sympy as sym
t, f = sym.symbols('t, f', real=True)
a, b = sym.symbols('a, b', real=True, positive=True)
x = sym.Function('x')
y = sym.Function('y')
i = sym.I
π = sym.pi
A = sym.integrate(( a*x(t) + b*y(t) )*sym.exp(-i*2*π*f*t), (t, -sym.oo, +sym.oo))
A
Izraz razširimo; ker sta \(a\) in \(b\) konstanti, potrdimo linearnost:
sym.expand(A)
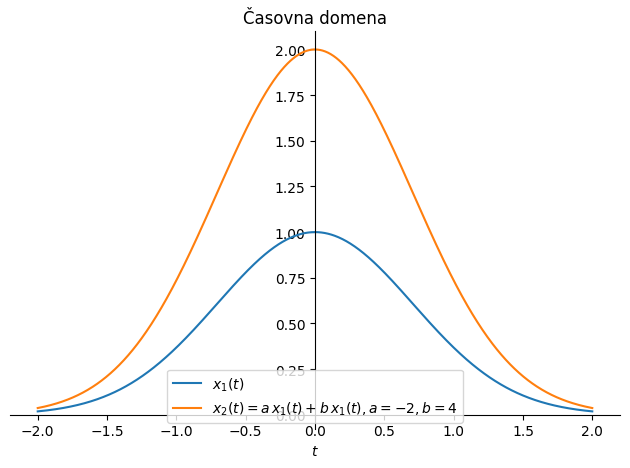
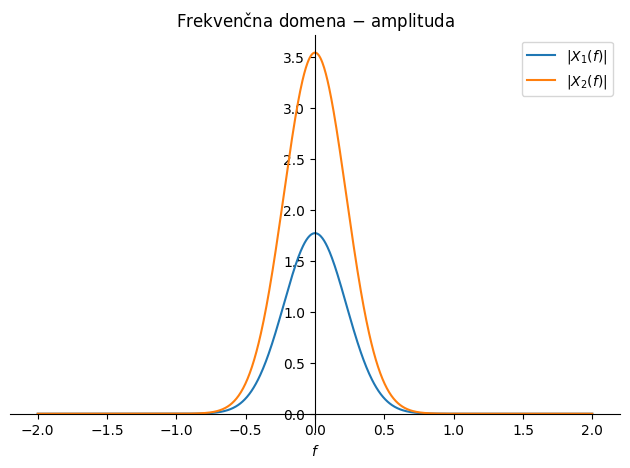
Spodaj si poglejmo konkreten primer.
Show code cell source
import sympy as sym
t, f, a, b = sym.symbols('t, f, a, b', real=True)
x_1 = sym.exp(-t**2)
x_2 = a * x_1 + b*x_1
podatki = {a: -2, b:4}
X_1 = sym.fourier_transform(x_1, t, f)
X_2 = sym.fourier_transform(x_2.subs(podatki), t, f)
p1 = sym.plot(x_1.subs(podatki), (t, -2, +2), line_color='C0',
label=f'$x_1(t)$', show=False,
title='Časovna domena', ylabel='', xlabel='$t$')
p2 = sym.plot(x_2.subs(podatki), (t, -2, +2), line_color='C1',
label=f'$x_2(t)=a\\,x_1(t)+b\\,x_1(t), a={a.subs(podatki)}, b={b.subs(podatki)}$', show=False)
p1.extend(p2)
p1.legend = True
p1.show()
p1 = sym.plot(sym.Abs(X_1).subs(podatki), (f, -2, +2), line_color='C0',
label=f'$|X_1(f)|$', show=False,
title='Frekvenčna domena $-$ amplituda', ylabel='', xlabel='$f$')
p2 = sym.plot(sym.Abs(X_2).subs(podatki), (f, -2, +2), line_color='C1',
label='$|X_2(f)|$', show=False)
p1.extend(p2)
p1.legend = True
p1.show()
Časovno skaliranje (ang. time scaling)#
Opomba
Časovno skaliranje je definirano kot \(a\,t\) in ima na Fourierovo transformacijo vpliv:
Še izpeljava (za pozitivni \(a\)):
import sympy as sym
t, f, τ = sym.symbols('t, f, tau', real=True)
a = sym.symbols('a', real=True, positive=True)
x = sym.Function('x')
i = sym.I
π = sym.pi
X = sym.integrate(x(a*t)*sym.exp(-i*2*π*f*t), (t, -sym.oo, +sym.oo))
sym.Eq(X, X.transform(a*t, τ))
Časovno skaliranje npr. postane pomembno takrat, ko isto dogajanje spremljamo z dvema različnima urama.
Show code cell source
import sympy as sym
t, f, a = sym.symbols('t, f, a', real=True)
x_1 = sym.exp(-t**2)
x_2 = x_1.subs(t, a*t)
podatki = {a: 1.1}
X_1 = sym.fourier_transform(x_1, t, f)
X_2 = sym.fourier_transform(x_2.subs(podatki), t, f)
p1 = sym.plot(x_1.subs(podatki), (t, -2, +2), line_color='C0',
label=f'$t=t$', show=False,
title='Časovna domena', ylabel='$x(t)$', xlabel='$t$')
p2 = sym.plot(x_2.subs(podatki), (t, -2, +2), line_color='C1',
label=f'$t=a\\,t$, $a=${a.subs(podatki):3.2f}', show=False)
p1.extend(p2)
p1.legend = True
p1.show()
p1 = sym.plot(sym.Abs(X_1).subs(podatki), (f, -2, +2), line_color='C0',
label=f'$t=t$', show=False,
title='Frekvenčna domena $-$ amplituda', ylabel='$|X(f)|$', xlabel='$f$')
p2 = sym.plot(sym.Abs(X_2).subs(podatki), (f, -2, +2), line_color='C1',
label=f'$t=a\\,t$, $a=${a.subs(podatki):3.2f}', show=False)
p1.extend(p2)
p1.legend = True
p1.show()
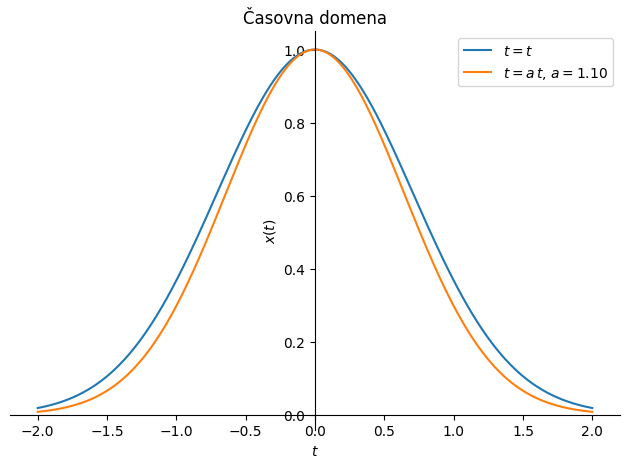
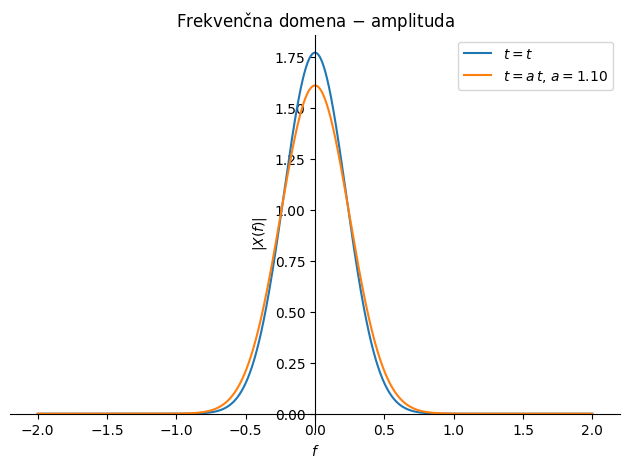
Fourierova transformacija časovno skalirane funkcije je enaka ustrezno korigirani neskalirani Fourierovi transformiranki:
X_2
(X_1/a).subs(f, f/a).subs(podatki)
Časovni obrat (ang. time reversal)#
Opomba
Časovni obrat ima na Fourierovo transformacijo vpliv:
Še izpeljava:
import sympy as sym
t, f, τ = sym.symbols('t, f, tau', real=True)
a = sym.symbols('a', real=True, positive=True)
x = sym.Function('x')
i = sym.I
π = sym.pi
X = sym.integrate(x(-t)*sym.exp(-i*2*π*f*t), (t, -sym.oo, +sym.oo))
sym.Eq(X, X.transform(-t, τ))
Časovni premik (ang. time shifting)#
Opomba
Časovni premik je definiran s \(t_0\) in ima na Fourierovo transformacijo vpliv:
Še izpeljava:
import sympy as sym
t, t_0, f, τ = sym.symbols('t, t_0, f, tau', real=True)
a = sym.symbols('a', real=True, positive=True)
x = sym.Function('x')
i = sym.I
π = sym.pi
X = sym.integrate(x(t-t_0)*sym.exp(-i*2*π*f*t), (t, -sym.oo, +sym.oo))
sym.Eq(X, X.transform(t-t_0, τ))
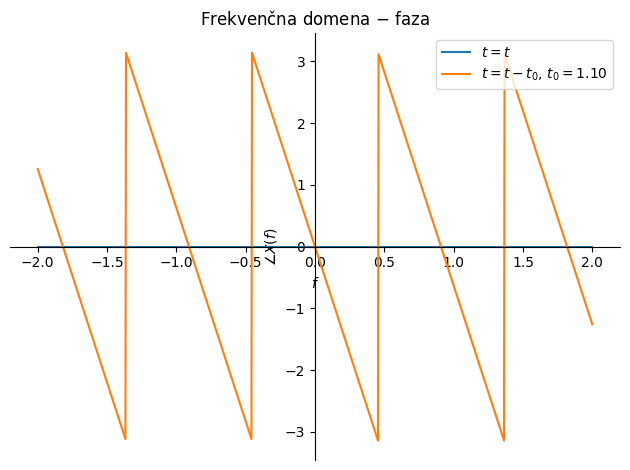
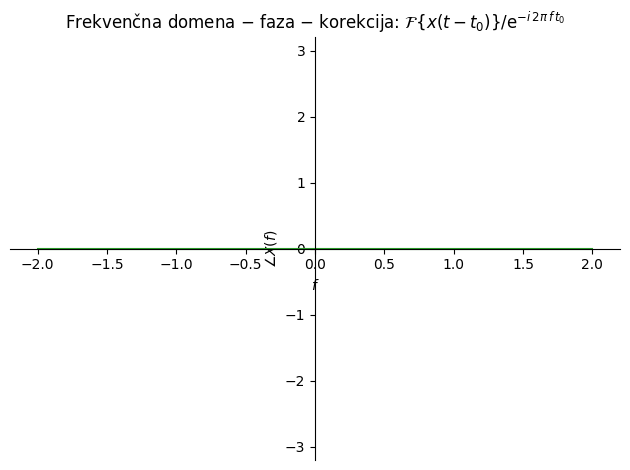
Opazimo, da člen \(\mathrm{e}^{-\textrm{i}\,2\pi\,f\,t_0}\) lahko izpostavimo iz integrala.
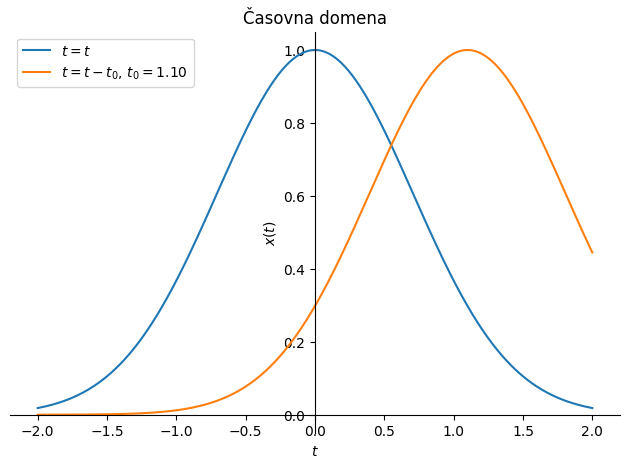
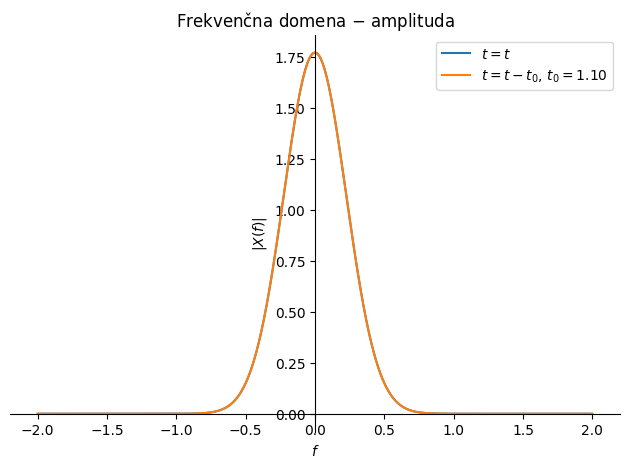
Časovni premik postane pomemben, kadar obravnavamo zakasnjene meritve (npr. če eno meritev merimo z zakasnitvijo glede na ostale): glejte primer spodaj.
Show code cell source
import sympy as sym
t, t_0, f, a = sym.symbols('t, t_0, f, a', real=True)
i = sym.I
π = sym.pi
x_1 = sym.exp(-t**2)
x_2 = x_1.subs(t, t-t_0)
podatki = {t_0: 1.1}
X_1 = sym.fourier_transform(x_1, t, f)
X_2 = sym.fourier_transform(x_2.subs(podatki), t, f)
X_3 = X_2/sym.exp(-i*2*π*f*t_0)
p1 = sym.plot(x_1.subs(podatki), (t, -2, +2), line_color='C0',
label=f'$t=t$', show=False,
title='Časovna domena', ylabel='$x(t)$', xlabel='$t$')
p2 = sym.plot(x_2.subs(podatki), (t, -2, +2), line_color='C1',
label=f'$t=t-t_0$, $t_0=${t_0.subs(podatki):3.2f}', show=False)
p1.extend(p2)
p1.legend = True
p1.show()
p1 = sym.plot(sym.Abs(X_1).subs(podatki), (f, -2, +2), line_color='C0',
label=f'$t=t$', show=False,
title='Frekvenčna domena $-$ amplituda', ylabel='$|X(f)|$', xlabel='$f$')
p2 = sym.plot(sym.Abs(X_2).subs(podatki), (f, -2, +2), line_color='C1',
label=f'$t=t-t_0$, $t_0=${t_0.subs(podatki):3.2f}', show=False)
p1.extend(p2)
p1.legend = True
p1.show()
p1 = sym.plot(sym.arg(X_1).subs(podatki), (f, -2, +2), line_color='C0',
label=f'$t=t$', show=False,
title='Frekvenčna domena $-$ faza', ylabel='$\\angle X(f)$', xlabel='$f$')
p2 = sym.plot(sym.arg(X_2).subs(podatki), (f, -2, +2), line_color='C1',
label=f'$t=t-t_0$, $t_0=${t_0.subs(podatki):3.2f}', show=False)
p1.extend(p2)
p1.legend = True
p1.show()
p1 = sym.plot(sym.arg(X_3).subs(podatki), (f, -2, +2), line_color='C2',
label=f'$t=t$', show=True, ylim=[-3.2, 3.2],
title='Frekvenčna domena $-$ faza $-$ korekcija: $\\mathcal{F}\\{x(t-t_0)\\} / \\mathrm{e}^{-i\\,2\\pi\\,f\\,t_0}$', ylabel='$\\angle X(f)$', xlabel='$f$')
p1.legend = True
Amplitudna modulacija (ang. modulation, tudi frequency-shifting)#
Opomba
Amplitudna modulacija je definirana z \(\mathrm{e}^{\textrm{i}\,2\pi\,f_0\,t}\) in ima na Fourierovo transformacijo vpliv:
Amplitudno modulacijo srečamo tudi v obliki, pomnoženi s kosinusno funkcijo:
Še izpeljava:
import sympy as sym
t, f, τ = sym.symbols('t, f, tau', real=True)
f_0 = sym.symbols('f_0', real=True, positive=True)
x = sym.Function('x')
i = sym.I
π = sym.pi
X = sym.integrate(x(t)*sym.exp(i*2*π*f_0*t)*sym.exp(-i*2*π*f*t), (t, -sym.oo, +sym.oo))
sym.Eq(X, sym.simplify(X))
Amplitudna modulacija je v praksi relativno pogosta. Opazimo jo na primer, ko merimo nihanje plošče z laserjem in se nam podlaga laserja trese; v spodnjih slikah je pomik merjene strukture označen z \(x(t)\), podlaga laserja pa niha s \(\cos(2\pi\,f_0\,t)\).
Show code cell source
import sympy as sym
t, f = sym.symbols('t, f', real=True)
f_0 = sym.symbols('f_0', real=True, positive=True)
i = sym.I
π = sym.pi
x_1 = sym.exp(-t**2)
x_2 = x_1*sym.cos(2*π*f_0*t)
podatki = {f_0: 1}
X_1 = sym.fourier_transform(x_1, t, f)
X_2 = sym.fourier_transform(x_2.subs(podatki), t, f)
X_1 = sym.fourier_transform(x_1, t, f)
X_2 = sym.fourier_transform(x_2.subs(podatki), t, f)
p1 = sym.plot(x_1.subs(podatki), (t, -2, +2), line_color='C0',
label=f'$x(t)$', show=False,
title='Časovna domena', ylabel='$x(t)$', xlabel='$t$')
p2 = sym.plot(x_2.subs(podatki), (t, -2, +2), line_color='C1',
label=f'$x(t)\\,\\cos(2\\pi\\,f_0\\,t)$', show=False)
p1.extend(p2)
p1.legend = True
p1.show()
p1 = sym.plot(sym.Abs(X_1).subs(podatki), (f, -2, +2), line_color='C0',
label='$\\mathcal{F}\\{x(t)\\}$', show=False,
title='Frekvenčna domena $-$ amplituda', ylabel='$|X(f)|$', xlabel='$f$')
p2 = sym.plot(sym.Abs(X_2).subs(podatki), (f, -2, +2), line_color='C1',
label='$\\mathcal{F}\\{x(t)\\,\\cos(2\\pi\\,f_0\\,t)\\}$', show=False)
p1.extend(p2)
p1.legend = True
p1.show()
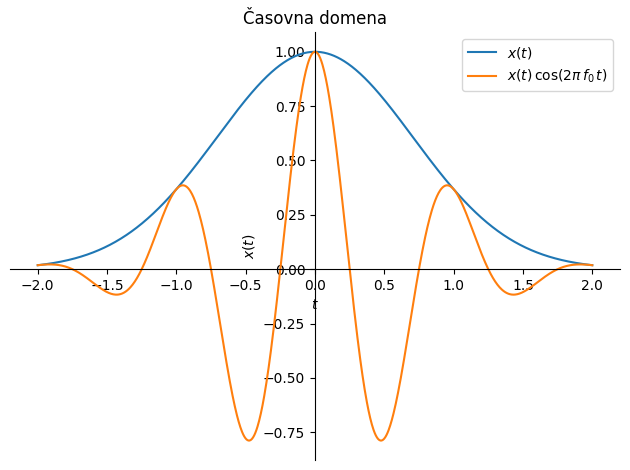
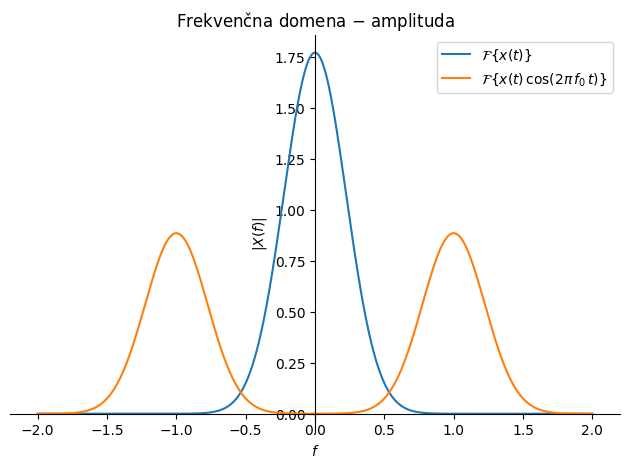
Mimogrede: amplitudna modulacija (AM) in frekvenča modulacija (FM) sta klasična načina prenosa informacij (npr. radijskega signala).
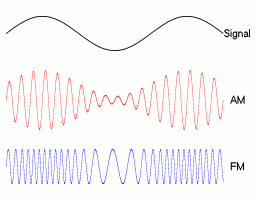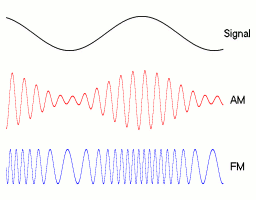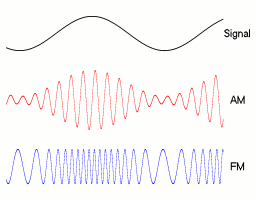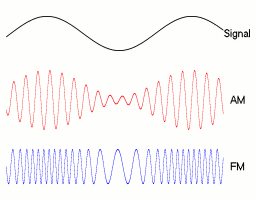
Odvajanje#
Opomba
Če je \(\dot{x}(t)\) časovni odvod \(x(t)\), je njuna relacija v frekvenčni domeni:
kjer velja predpostavka, da gre \(x(t)\rightarrow 0\), ko gre \(t\rightarrow \pm\infty\).
Še izpeljava:
import sympy as sym
t, f = sym.symbols('t, f', real=True)
x = sym.Function('x')
i = sym.I
π = sym.pi
X = sym.integrate(sym.diff(x(t),t)*sym.exp(-i*2*π*f*t), (t, -sym.oo, +sym.oo))
X
Uporabiti moramo integriranje po delih \(u = \mathrm{e}^{-\textrm{i}\,2\pi\,f\,t}\), \(\textrm{d}v= \dot{x}(t)\,\textrm{d}t\); pripravimo \(\textrm{d}u\) in \(v\):
u = sym.exp(-i*2*π*f*t)
dv = sym.diff(x(t),t)
du = sym.diff(u, t)
v = sym.integrate(dv, t)
Sledi, da moramo izraz (prvi del integriranja po delih):
u*v
izračunati ob mejah \(+\infty\) in \(-\infty\); glede na definicijo zgoraj v obeh primerih (zaradi predhodne predpostavke) velja \(x(t=\pm \infty)=0\).
Preostane torej samo še drugi del integriranja po delih:
sym.integrate(v*du, (t, -sym.oo, +sym.oo))
in s tem smo dokaz zaključili.
Integriranje#
Opomba
Če je \(\int_{-\infty}^t x(\tau)\,\textrm{d}\tau\) integral funkcije \(x(t)\), je njuna relacija v frekvenčni domeni:
Izpeljava za integriranje sledi iz tiste za odvajanje:
pri čemer naredimo zamenjavo funkcije: \(u(t)=\dot{x}(t)\) in \(\int_{-\infty}^t u(\tau)\,\textrm{d}\tau=x(t)\).
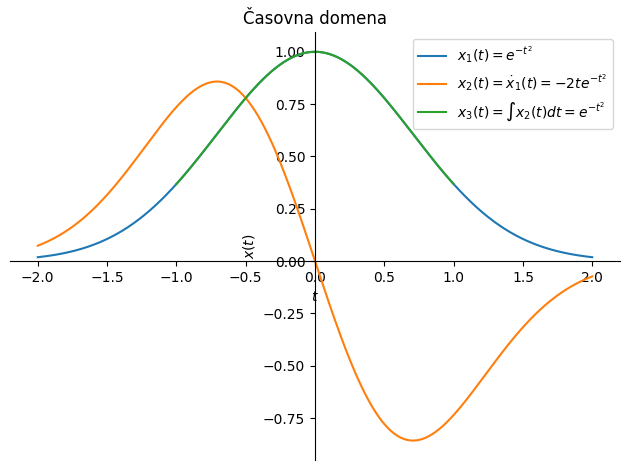
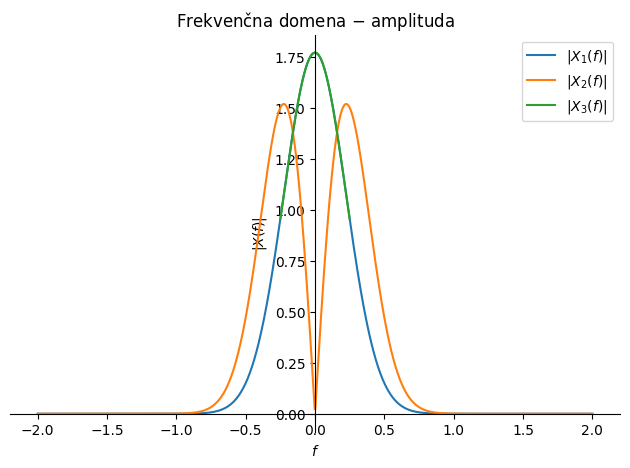
Odvajanje in integriranje v frekvenčni domeni sta zelo pomembni lastnosti Fourierove transformacije, saj nam omogočata enostaven prehod med odvajanimi in integriranimi podatki.
Tukaj velja poudariti, da je časovno odvajanje negotova numerična operacija, saj temelji na majhni razliki števil (razlika pa se nato deli z majhnim številom, kar dodatno povečuje negotovost). Odvajanje v frekvenčni domeni taki negotovosti ni izpostavljeno.
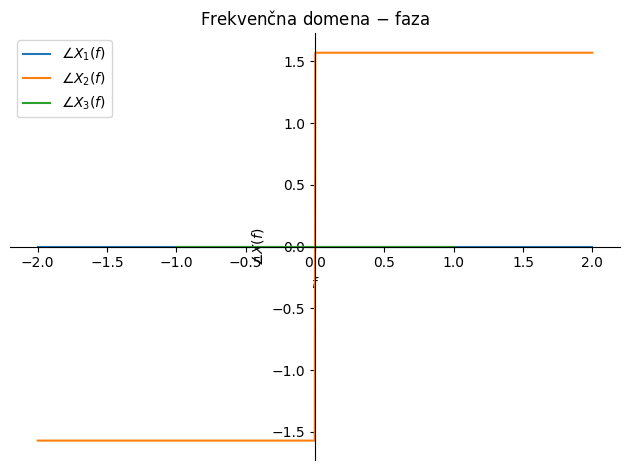
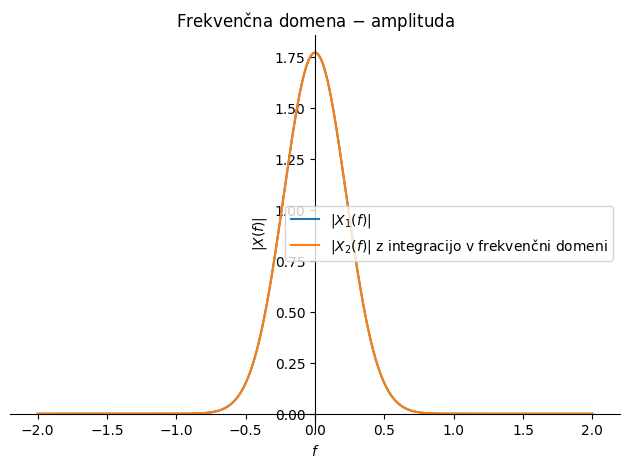
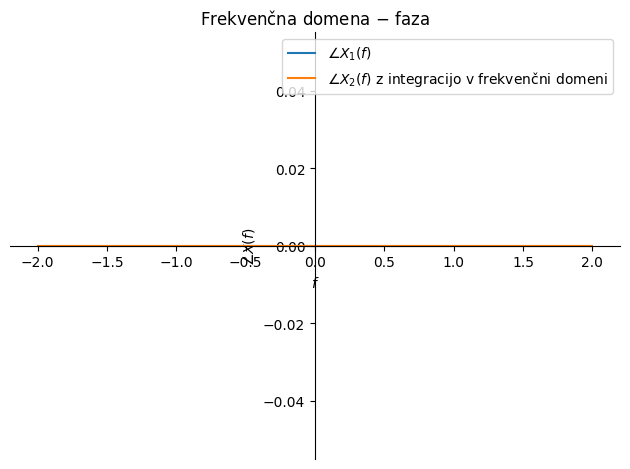
Nadalje poudarimo, da je časovno integriranje nestabilna numerična operacija, saj se napaka posameznega koraka sešteva in zato s časom raste. Integracija v frekvenčni domeni taki nestabilnosti ni izpostavljena; res pa je, da imamo pri frekvenci 0 Hz nedoločen rezultat (deljenje z 0).
Show code cell source
import sympy as sym
t, f = sym.symbols('t, f', real=True)
i = sym.I
π = sym.pi
x_1 = sym.exp(-t**2)
x_2 = sym.diff(x_1, t)
x_3 = sym.integrate(x_2, t)
X_1 = sym.fourier_transform(x_1, t, f)
X_2 = sym.fourier_transform(x_2, t, f)
X_3 = sym.fourier_transform(x_3, t, f)
p1 = sym.plot(x_1, (t, -2, +2), line_color='C0',
label=f'$x_1(t)={sym.latex(x_1)}$', show=False,
title='Časovna domena', ylabel='$x(t)$', xlabel='$t$')
p2 = sym.plot(x_2, (t, -2, +2), line_color='C1',
label=f'$x_2(t)=\\dot x_1(t)={sym.latex(x_2)}$', show=False)
p3 = sym.plot(x_3, (t, -1, +1), line_color='C2',
label=f'$x_3(t)=\\int x_2(t)dt={sym.latex(x_3)}$', show=False)
p1.extend(p2)
p1.extend(p3)
p1.legend = True
p1.show()
p1 = sym.plot(sym.Abs(X_1), (f, -2, +2), line_color='C0',
label=f'$|X_1(f)|$', show=False,
title='Frekvenčna domena $-$ amplituda', ylabel='$|X(f)|$', xlabel='$f$')
p2 = sym.plot(sym.Abs(X_2), (f, -2, +2), line_color='C1',
label=f'$|X_2(f)|$', show=False)
p3 = sym.plot(sym.Abs(X_3), (f, -.25, +.25), line_color='C2',
label=f'$|X_3(f)|$', show=False)
p1.extend(p2)
p1.extend(p3)
p1.legend = True
p1.show()
p1 = sym.plot(sym.arg(X_1), (f, -2, +2), line_color='C0',
label=f'$\\angle X_1(f)$', show=False,
title='Frekvenčna domena $-$ faza', ylabel='$\\angle X(f)$', xlabel='$f$')
p2 = sym.plot(sym.arg(X_2), (f, -2, +2), line_color='C1',
label=f'$\\angle X_2(f)$', show=False)
p3 = sym.plot(sym.arg(X_3), (f, -1, +1), line_color='C2',
label=f'$\\angle X_3(f)$', show=False)
p1.extend(p2)
p1.extend(p3)
p1.legend = True
p1.show()
p1 = sym.plot(sym.Abs(X_1), (f, -2, +2), line_color='C0',
label=f'$|X_1(f)|$', show=False,
title='Frekvenčna domena $-$ amplituda', ylabel='$|X(f)|$', xlabel='$f$')
p2 = sym.plot(sym.Abs(X_2/(2*i*π*f)), (f, -2, +2), line_color='C1',
label=f'$|X_2(f)|$ z integracijo v frekvenčni domeni', show=False)
p1.extend(p2)
p1.legend = True
p1.show()
p1 = sym.plot(sym.arg(X_1), (f, -2, +2), line_color='C0',
label=f'$\\angle X_1(f)$', show=False,
title='Frekvenčna domena $-$ faza', ylabel='$\\angle X(f)$', xlabel='$f$')
p2 = sym.plot(sym.arg(X_2/(2*i*π*f)), (f, -2, +2), line_color='C1',
label=f'$\\angle X_2(f)$ z integracijo v frekvenčni domeni', show=False)
p1.extend(p2)
p1.legend = True
p1.show()
Konvolucija funkcij#
Opomba
Fourierova transformacija konvolucije dveh funkcij je enaka produktu Fourierovih transformirank:
Znak \(*\) označuje konvolucijo:
Zgornjo povezavo izpeljemo:
import sympy as sym
t, f, τ, v = sym.symbols('t, f, tau, v', real=True)
x = sym.Function('x')
y = sym.Function('y')
i = sym.I
π = sym.pi
X = sym.integrate(
sym.integrate(x(τ)*y(t-τ)*sym.exp(-i*2*π*f*t), (τ, -sym.oo, +sym.oo)),
(t, -sym.oo, +sym.oo))
X
Uvedemo še novo spremenljivko:
X = X.transform(t-τ, v)
X
Zgoraj je očitno, da lahko integral po \(\tau\) in \(v\) ločimo, ločeni integral pa predstavlja Fourierovo transformiranko \(X(f)\) in \(Y(f)\).
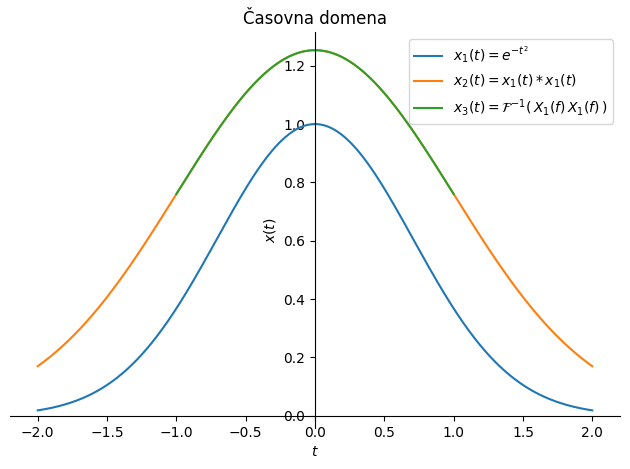
Fourierova transformacija konvolucije je mogoče najbolj uporabna lastnost Fourierove transformacije, saj množenje v frekvenčni domeni bistveno pohitri izračun konvolucije dveh funkcij. Lastnost bomo s pridom uporabljali pri diskretni Fourierovi transformaciji, preprost primer spodaj pa pokaže ekvivalentnost rezultata v času napram tistemu v frekvenci.
Show code cell source
import sympy as sym
t, f, τ = sym.symbols('t, f, τ', real=True)
i = sym.I
π = sym.pi
x_1 = sym.exp(-t**2)
x_2 = sym.integrate(x_1.subs(t,τ)*x_1.subs(t,t-τ), (τ, -sym.oo, +sym.oo)) # konvolucija v času
X_1 = sym.fourier_transform(x_1, t, f)
X_2 = sym.fourier_transform(x_2, t, f)
X_3 = X_1*X_1 # produkt v frekvenčni domeni
x_3 = sym.inverse_fourier_transform(X_2, f, t)
p1 = sym.plot(x_1, (t, -2, +2), line_color='C0',
label=f'$x_1(t)={sym.latex(x_1)}$', show=False,
title='Časovna domena', ylabel='$x(t)$', xlabel='$t$')
p2 = sym.plot(x_2, (t, -2, +2), line_color='C1',
label=f'$x_2(t)=x_1(t)*x_1(t)$', show=False)
p3 = sym.plot(x_3, (t, -1., +1.), line_color='C2',
label='$x_3(t)=\\mathcal{F}^{-1}(\\,X_1(f)\\,X_1(f)\\,)$', show=False)
p1.extend(p2)
p1.extend(p3)
p1.legend = True
p1.show()
p1 = sym.plot(sym.Abs(X_1), (f, -2, +2), line_color='C0',
label=f'$|X_1(f)|$', show=False,
title='Frekvenčna domena $-$ amplituda', ylabel='$|X(f)|$', xlabel='$f$')
p2 = sym.plot(sym.Abs(X_2), (f, -2, +2), line_color='C1',
label=f'$|X_2(f)|$', show=False)
p3 = sym.plot(sym.Abs(X_1*X_1), (f, -.25, +.25), line_color='C2',
label=f'$|X_1(f)\\,X_1(f)|$', show=False)
p1.extend(p2)
p1.extend(p3)
p1.legend = True
p1.show()
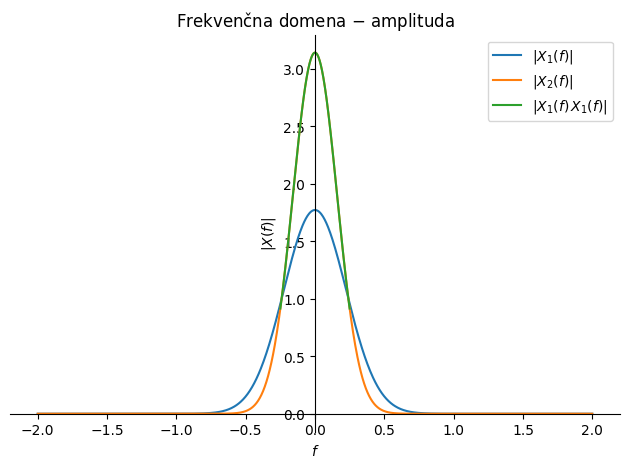
Produkt funkcij#
Opomba
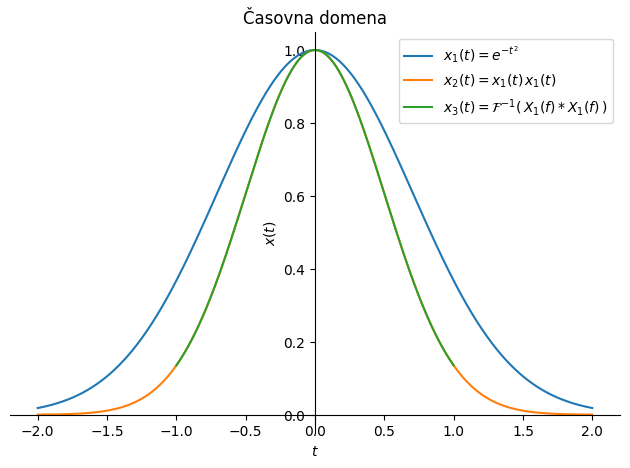
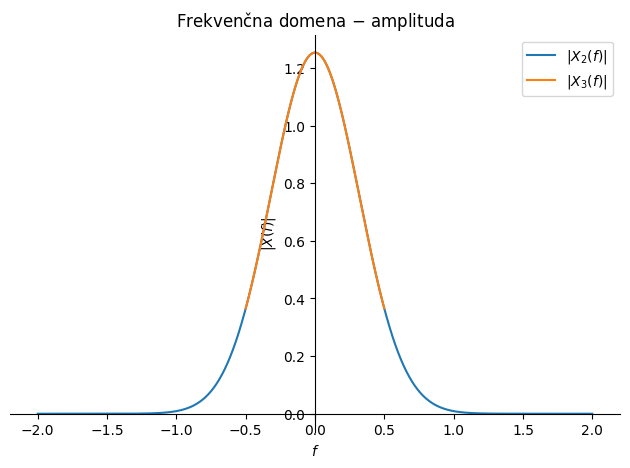
Fourierova transformacija produkta dveh funkcij v frekvenčni domeni predstavlja konvolucijo Fourierovih transformirank:
Zgornjo povezavo izpeljemo:
Sedaj upoštevamo \(\int_{-\infty}^{+\infty}\mathrm{e}^{\pm\textrm{i}\,2\pi\,a\,t}\,\textrm{d}t= \delta(a)\) (glejte Lastnosti Diracove delta funkcije) in dokažemo zgornjo izpeljavo:
Spodaj si poglejmo še konkreten zgled.
Show code cell source
import sympy as sym
t, f, f_1 = sym.symbols('t, f, f_1', real=True)
i = sym.I
π = sym.pi
x_1 = sym.exp(-t**2)
x_2 = x_1*x_1
X_1 = sym.fourier_transform(x_1, t, f)
X_2 = sym.fourier_transform(x_2, t, f) # produkt v času
X_3 = sym.integrate(X_1.subs(f, f_1)*X_1.subs(f, f-f_1), (f_1, -sym.oo, +sym.oo)) # konvolucija v frekvenci
x_3 = sym.inverse_fourier_transform(X_3, f, t)
p1 = sym.plot(x_1, (t, -2, +2), line_color='C0',
label=f'$x_1(t)={sym.latex(x_1)}$', show=False,
title='Časovna domena', ylabel='$x(t)$', xlabel='$t$')
p2 = sym.plot(x_2, (t, -2, +2), line_color='C1',
label=f'$x_2(t)=x_1(t)\\,x_1(t)$', show=False)
p3 = sym.plot(x_3, (t, -1., +1.), line_color='C2',
label='$x_3(t)=\\mathcal{F}^{-1}(\\,X_1(f)*X_1(f)\\,)$', show=False)
p1.extend(p2)
p1.extend(p3)
p1.legend = True
p1.show()
p1 = sym.plot(sym.Abs(X_2), (f, -2, +2), line_color='C0',
label=f'$|X_2(f)|$', show=False,
title='Frekvenčna domena $-$ amplituda', ylabel='$|X(f)|$', xlabel='$f$')
p2 = sym.plot(sym.Abs(X_3), (f, -.5, +.5), line_color='C1',
label=f'$|X_3(f)|$', show=False)
p1.extend(p2)
p1.legend = True
p1.show()
Uporaba oken#
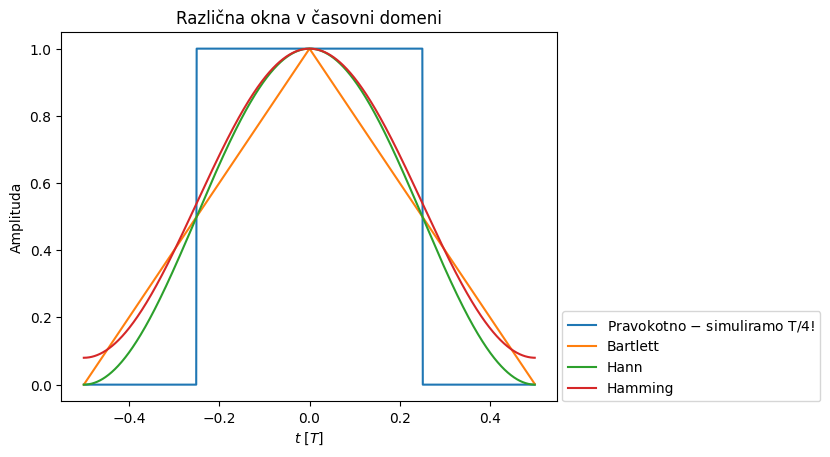
Predpostavimo, da želimo izračunati Fourierovo transformacijo determinističnega signala \(x(t)\), ki je načeloma definiran od \(-\infty\) do \(+\infty\), vendar pa ga gledamo samo na območju od \(-T/2\) do \(+T/2\). Dobimo naslednje podatke:
kjer je:
Če pridobimo Fourierovo transformacijo \(x_T(t)\), velja:
Sporočilo torej je: \(X(f)\) predstavlja frekvenčno transformiranko funkcije \(x(t)\), ki jo lahko gledamo samo v nekem časovno omejenem oknu \(w(t)\), le-to pa povzroči, da je Fourierova transformacija popačena. Pravokotni impulz \(w(t)\) smo si že pogledali zgoraj (Pravokotni impulz) in ugotovili, da je frekvenčna transformiranka definirana kot:
kjer smo uporabili zapis, ki razkrije limito, ko gre \(T\to 0\), gre: \(W(0)=T\).
Show code cell source
import numpy as np
import matplotlib.pyplot as plt
A = 1
T = 1.
N = 1000
t = np.linspace(-T/2, T/2, N, endpoint=False)
dt = t[1] - t[0]
# pravokotno
wp = np.ones_like(t)
Tp = 0.5*T/2 # teoretično bi tukaj morali vzeti 1*T/2
wp[np.abs(t)>Tp] = 0
fT_teor = np.arange(-10,10,0.01)
Wp_teor = A*T / (np.pi*fT_teor) * np.sin(np.pi*fT_teor)
# Bartlett
wBartlett = np.ones_like(t)
wBartlett = A*(wBartlett-np.abs(t)/(T/2))
WBartlett_teor = 0.5*A*T * np.power(np.sin(0.5*np.pi*fT_teor) / (0.5*np.pi*fT_teor),2)
# Hann
wHann = A*np.power(np.cos(np.pi*t/T), 2)
WHann_teor = 0.5*A*T * np.sin(np.pi*fT_teor) / (np.pi*fT_teor*(1-fT_teor**2))
# Hamming
wHamming = 0.54+0.46*np.cos(2*np.pi*t/T)
WHamming_teor = (0.54*np.pi**2-0.08*(np.pi*fT_teor)**2)*np.sin(np.pi*fT_teor)/(np.pi*fT_teor*(np.pi**2-(np.pi*fT_teor)**2))
plt.plot(t,wp,'C0', label='Pravokotno $-$ simuliramo T/4!')
plt.plot(t,wBartlett,'C1', label='Bartlett')
plt.plot(t,wHann,'C2', label='Hann')
plt.plot(t,wHamming,'C3', label='Hamming')
plt.title('Različna okna v časovni domeni')
plt.xlabel('$t$ [$T$]')
plt.ylabel('Amplituda')
plt.legend(loc=(1.01, 0));
plt.show()
narisi = plt.plot
# narisi = plt.semilogy # s to opcijo je treba popraviti ylim
plt.vlines(np.arange(-5,6), 0,1, 'k', lw=1, alpha=0.5)
narisi(fT_teor, Wp_teor, 'C0', label='Pravokotno')
narisi(fT_teor, WBartlett_teor, 'C1', label='Bartlett')
narisi(fT_teor, WHann_teor, 'C2', label='Hann')
narisi(fT_teor, WHamming_teor, 'C3', label='Hamming')
plt.xlim(-5,5)
plt.title('Različna okna v frekvenčni domeni')
plt.xlabel('$f$ [1/T]')
plt.ylabel('Amplituda')
plt.legend(loc=(1.01, 0));
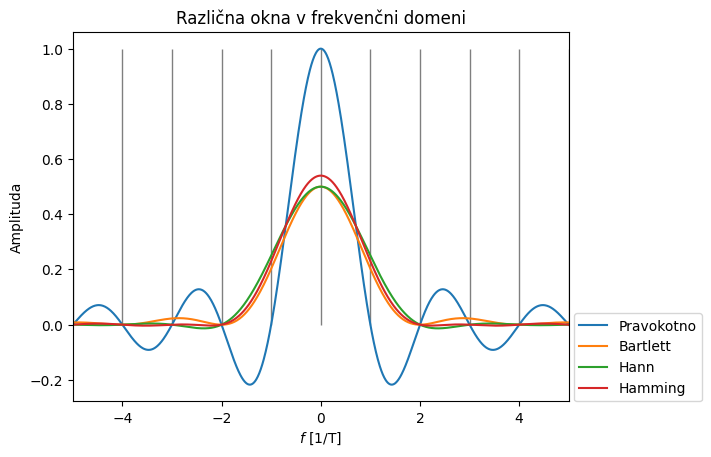
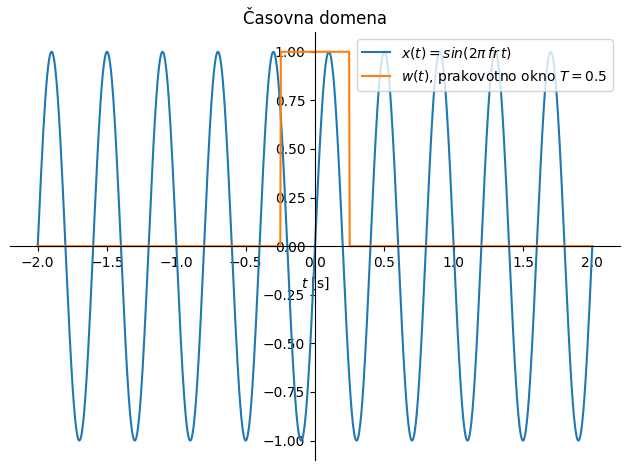
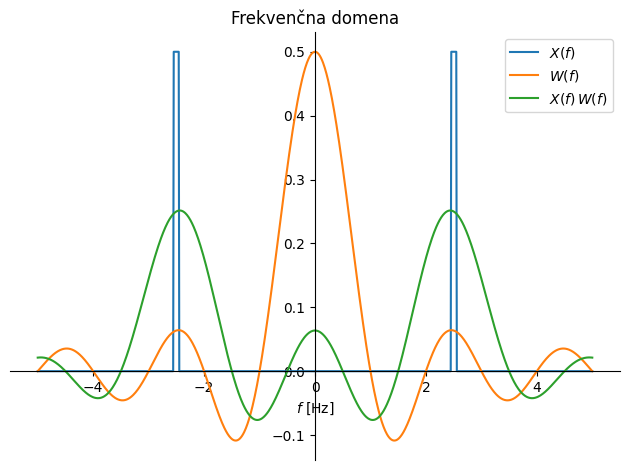
Za sinusoido frekvence fr z amplitudo 1 vemo, da ima v frekvenčni domeni amplitudo 1/2 pri frekvencah -fr in fr; po drugi strani smo zgoraj definirali frekvenčno funkcijo pravokotnega okna. Kako pravokotno okno popači sinusoido, si lahko ogledamo, tako da konvuliramo njuni frekvenčni transformiranki (primer spodaj).
Show code cell source
import sympy as sym
t, f, τ, fr, T = sym.symbols('t, f, τ, fr, T', real=True)
i = sym.I
π = sym.pi
podatki = {fr: 2.5, T: 0.5}
x = sym.sin(2*π*fr*t)
w = sym.Heaviside(t+T/2) - sym.Heaviside(t-T/2)
xw = x*w
X = 1/2 * sym.DiracDelta(f+fr) + 1/2 * sym.DiracDelta(f-fr)
W = T / (π*f) * sym.sin(π*f)
XW = sym.integrate(X.subs(f,τ)*W.subs(f,f-τ), (τ, -sym.oo, +sym.oo)) # konvolucija v frekvenci
p1 = sym.plot(x.subs(podatki), (t, -2, +2), line_color='C0',
label=f'$x(t)=sin(2\\pi\\,fr\\,t)$', show=False,
title='Časovna domena', ylabel='', xlabel='$t$ [s]')
p2 = sym.plot(w.subs(podatki), (t, -2, +2), line_color='C1',
label=f'$w(t)$, prakovotno okno $T={T.subs(podatki):3.1f}$', show=False)
p1.extend(p2)
p1.legend = True
p1.show()
p1 = sym.plot(0.5*(sym.Heaviside(f+(fr+0.05))-sym.Heaviside(f+(fr-0.05))+
sym.Heaviside(f-(fr-0.05))-sym.Heaviside(f-(fr+0.05))).subs(podatki),
(f, -5, +5), line_color='C0',
label=f'$X(f)$', show=False,
title='Frekvenčna domena', ylabel='', xlabel='$f$ [Hz]')
p2 = sym.plot(W.subs(podatki), (f, -5, +5), line_color='C1',
label=f'$W(f)$', show=False)
p3 = sym.plot(XW.subs(podatki), (f, -5, +5), line_color='C2',
label=f'$X(f)\\,W(f)$', show=False)
p1.extend(p2)
p1.extend(p3)
p1.legend = True
p1.show()