1. Uvod v procesiranje signalov#
Uvodno poglavje predstavi motivacijo za knjigo, definira nekatere termine in predstavi strukturo knjige.
Poglavja v knjigi so:
Kaj je procesiranje signalov?#
Termin procesiranje signalov uporabljamo za označitev različnih metod obdelave izmerjenih podatkov z namenom, da razkrijemo informacije obravnavanega sistema. Potencialno bi lahko govorili tudi o obdelavi podatkov, vendar je takšen termin po eni strani preširok, po drugi strani pa preozek. Preširok zato, ker se s procesiranjem signalov želimo omejiti na identifikacijo/karakterizacijo različnih inženirskih sistemov in ne nasloviti splošne obdelave poljubnih podatkov. Preozek pa zato, ker so podatki vedno diskretni, procesiranje pa se lahko začne že na signalih, ki so lahko zvezni ali diskretni.
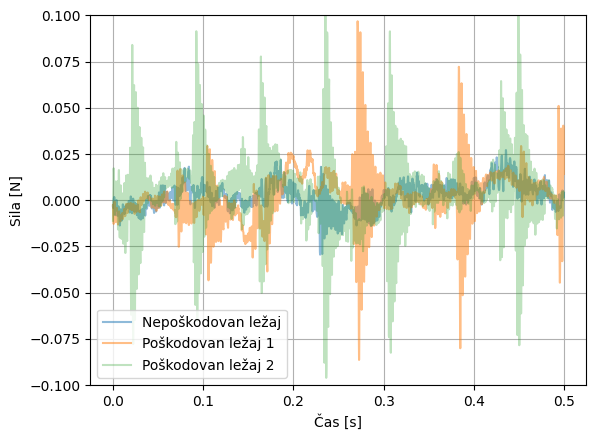
Kot primer procesiranja signalov lahko izpostavimo identifikacijo napak na ležajih ali identifikacijo dinamskih lastnosti struktur (npr. dušenje, togost). V obeh primerih moramo merjene signale pravilno obdelati, že preden jih časovno vzorčimo in nato kvantiziramo (glejte 5. Kvantizacija podatkov). Slika spodaj prikazuje meritev sile na nepoškodovanem in dveh poškodovanih ležajih (Slavič et al. [2011]). V meritvah vidimo določene razlike, ampak ali lahko iz meritev identificiramo tip poškodbe? Nadalje, ali lahko iz meritev identificiramo velikost poškodbe? Na ta in podobna vprašanja bomo poskušali odgovoriti v tej knjigi.
Show code cell source
import numpy as np
import matplotlib.pyplot as plt
new = np.load('./data/bearing/new 1A.npy')
radial = np.load('./data/bearing/radial Low 1A.npy')
contamination = np.load('./data/bearing/contam low 2A.npy')
time = np.arange(len(new)) * 1./5000
sel = time<0.5
plt.plot(time[sel], new[sel, 2], alpha=0.5, label='Nepoškodovan ležaj')
plt.plot(time[sel], radial[sel, 2], alpha=0.5, label='Poškodovan ležaj 1')
plt.plot(time[sel], contamination[sel, 2], alpha=0.3, label='Poškodovan ležaj 2')
plt.xlabel('Čas [s]')
plt.ylabel('Sila [N]')
plt.ylim(-0.1, 0.1)
plt.grid()
plt.legend()
plt.show()
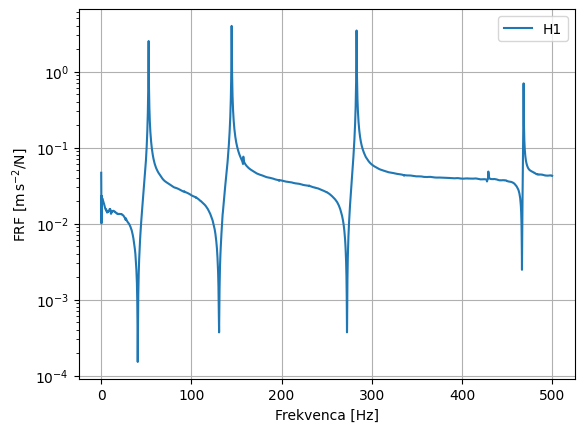
Kot naslednji primer je spodaj prikazana slika frekvenčne prenosne funkcije (ang. Frequency Response Function \(-\) FRF), ki v frekvenčni domeni povezuje vzbujanje sistema z njegovim odzivom (primer je vzet iz paketa pyUFF). Pravilna identifikacija frekvenčne prenosne funkcije je ključna za pravilno karakterizacijo dinamskih sistemov in zato tudi eden od temeljnih učnih ciljev te knjige.
Show code cell source
import numpy as np
import matplotlib.pyplot as plt
import pyuff
uff = pyuff.UFF('./data/uff/beam.uff').read_sets(setn=4)
fr = uff['x']
H1 = uff['data']
sel = fr<500
plt.semilogy(fr[sel], np.abs(H1[sel]), label='H1')
plt.xlabel('Frekvenca [Hz]')
plt.ylabel('FRF [m$\\,$s$^{-2}$/N]')
plt.grid()
plt.legend()
plt.show()
Kaj je sistem?#
Dinamske in druge sisteme ponavadi poskušamo opisati na podlagi modelov, parametre modelov pa identificirati s pomočjo eksperimentalnih meritev, ki jih ustrezno obdelamo. Spodnja slika prikazuje poljuben sistem, katerega vzbujanje opišemo v času z \(x(t)\), odziv pa z \(y(t)\). Kot primer vzbujanja sistema \(x(t)\) si lahko predstavljamo silo, ki deluje na neko maso, kot odziv \(y(t)\) pa napetost na zaznavalu pospeška ali zvočnega tlaka. Odziv je pogosto merjen prek električne napetosti, ki je ponavadi proporcionalna merjeni veličini (npr. pospešek, zvočni tlak); seveda pa je tako vzbujanje kot odziv lahko povezan tudi z drugimi veličinami, ki jih lahko merimo, npr. s tokom ali z intenziteto slikovnega elementa v sliki (glejte Gorjup et al. [2021]).
Sistem, natančneje linearni časovno invariantni sistem, bomo podrobno definirali v poglavju 4. Linearni časovno invariantni sistemi z eno prostostno stopnjo.
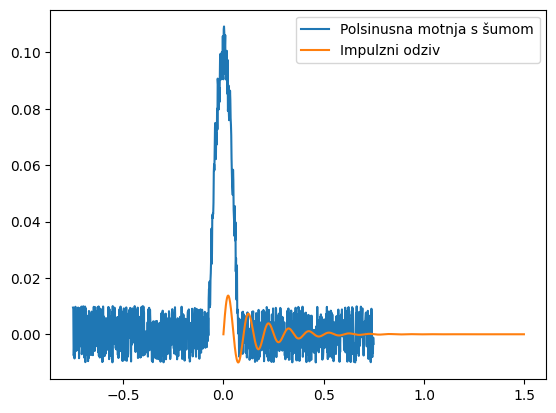
Kot primer si oglejmo odziv dinamskega sistema z eno prostostno stopnjo na polsinusno motnjo s šumom. Impulzna prenosna funkcija sistema z eno prostostno stopnjo je definirana kot:
Konkretno implementacijo in rezultat prikazuje koda spodaj.
Show code cell source
import numpy as np
import matplotlib.pyplot as plt
T = 1.5
N = 1000
w = 0.1
A = 0.1
t = np.linspace(-T/2, T/2, N, endpoint=False)
dt = t[1] - t[0]
x = A*np.cos(2*np.pi*t/(2*w*T))
x[np.logical_or(-w*T*0.5>t, t>w*T*0.5)] = 0.
x = x + 0.2*A*(np.random.rand(N)-0.5)
delta = 0.1 # damping ratio
omega0 = 2*np.pi*10
omega0d = omega0*np.sqrt(1-delta*delta)
th = dt*np.arange(len(x))
h = np.exp(-delta*omega0*th)*np.sin(omega0d*th)/omega0d
plt.plot(t,x, label='Polsinusna motnja s šumom')
plt.plot(th,h, label='Impulzni odziv')
plt.legend()
plt.show()
hx = np.convolve(h, x) # mode='full' -> sum of both arrays
plt.title('Odziv na polsinusno motnjo s šumom')
plt.plot(hx, 'C2')
plt.show()
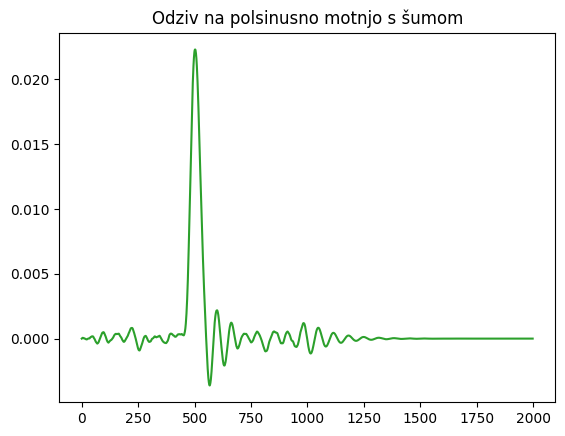
Da bomo lahko sisteme razumeli v časovni in frekvenčni domeni, bomo morali najprej spoznati pozneje predstavljene Fourierove vrste (2. Fourierove vrste) in Fourierovo integralsko transformacijo (3. Fourierova integralska transformacija).
Sistem lahko enolično identificiramo, če identificiramo frekvenčno prenosno fukcijo \(H(f)\) ali njen časovni par: impulzno prenosno funkcijo \(h(t)\). Če sta vzbujanje \(X(f)\) in odziv \(Y(f)\) v frekvenčni domeni znana, je identifikacija teoretično skrajno enostavna: \(H(f)=Y(f)/X(f)\). V praksi je problem v tem, da je meritev vzbujanja in odziva obremenjena z merilnimi in drugimi negotovostmi. Primer realnega sistema prikazuje spodnja slika; \(n_x(t)\) in \(n_y(t)\) predstavljata šum na strani vzbujanja in odziva, \(x_m(t)\) in \(y_m(t)\) pa izmerjeno vzbujanje in izmerjeni odziv (s šumom).
Izmerjeno vzbujanje \(x_m(t)\) je očitno drugačno od tistega, ki vzbuja sistem \(x(t)\), in izmerjeni odziv \(y_m(t)\) je očitno drugačen od dejanskega odziva \(y(t)\). Glede na merilne in druge negotovosti nimamo dostopa do dejanskega vzbujanja \(x(t)\) in dejanskega odziva \(y(t)\) in zato frekvenčne prenosne funkcije \(H(f)\) ne moremo določiti. V poglavju Cenilke frekvenčne prenosne funkcije si bomo pogledali, kako \(H(f)\) ocenimo na podlagi veličin, ki jih lahko izmerimo (\(x_m(t)\) in \(y_m(t)\)); takrat bomo govorili o cenilki frekvenčne prenosne funkcije \(\tilde{H}(f)\).
Zvezni/diskretni signali#
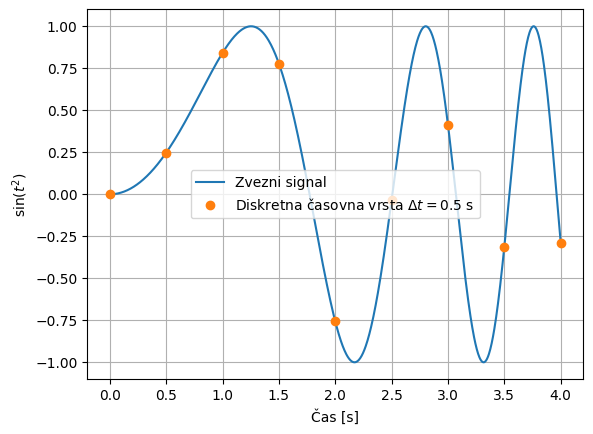
Inženirski procesi so ponavadi zvezni in jih zaznavamo s pomočjo različnih zaznaval, ki generirajo fizikalno merljivo veličino, t. i. signal. Signal je zvezna veličina (včasih bomo slišali tudi poimenovanje analogni signal). Ker podatke obdelujemo z računalnikom, te zvezne signale diskretiziramo (glejte poglavje Enakomerno časovno vzorčenje). Običajno je taka diskretizacija narejena s konstantnim časovnim korakom. Spodnja slika prikazuje zvezni signal in diskretno časovno vrsto.
Show code cell source
import numpy as np
import matplotlib.pyplot as plt
# na računalniku zvezne časovne vrste dejansko ne moremo generirati
# "zvezna" bo samo dosti bolj gosta
t, dt = np.linspace(0,4,1000, retstep=True)
t2, dt2 = np.linspace(0,4,9, retstep=True)
plt.plot(t, np.sin(t**2), label='Zvezni signal')
plt.plot(t2, np.sin(t2**2), 'o',label='Diskretna časovna vrsta $\\Delta t=$0.5 s')
plt.xlabel('Čas [s]')
plt.ylabel('$\\sin(t^2)$')
plt.grid()
plt.legend()
plt.show()
Klasifikacija signalov#
Za poznejšo obravnavo bo pomembna klasifikacija signalov (prirejeno po Bendat and Piersol [2011], Shin and Hammond [2008]), kakor jo prikazuje spodnja slika.
Signale delimo na:
deterministične (tudi določljivostne) \(-\) to so signali, ki imajo vrednosti v času enolično določene, in
naključne \(-\) to so signali, pri katerih vrednosti eksaktno ne vemo, lahko pa določimo verjetnostno porazdelitev.
Primer determinističnega signala predstavlja funkcija:
primer naključnega signala pa je meritev višine gladine razburkanega morja. Pri klasifikaciji signalov ne smemo pozabiti, da imamo lahko procese sestavljene iz determinističnega in naključnega dela (npr. meritev profila izdelka vključuje tudi naključno merilno napako).
Deterministične signale naprej delimo na periodične, ki se po določenemu času (periodi) ponovijo, in take, ki se ne ponovijo, torej neperiodične. Periodične delimo na harmonske, ki jih definira sinusoida poljubne fazne zakasnitve, in kompleksno periodične, ki jih definira vsota več harmonskih komponent. Pri kompleksno periodičnih signalih je pomembno, da je razmerje frekvenc harmonskih komponent racionalno število, saj se bo v tem primeru perioda ponavljala s periodo najmanjše skupne periode. Če razmerje harmonskih komponent ni racionalno število, govorimo o skoraj periodičnih signalih, ki pa spadajo v skupino neperiodičnih signalov. V to skupino spadajo še prehodni in kaotični signali.
Razumevanje periodičnosti signalov ter vpliva neperiodičnosti na Fourierove vrste (2. Fourierove vrste) in Fourierovo transformacijo (3. Fourierova integralska transformacija) je ključnega pomena za pravilno interpretacijo v frekvenčni domeni.
Naključne signale naprej delimo glede na to, ali se statistična porazdelitev, ki definira naključne procese, s časom spreminja (nestacionarni) ali pa ne (stacionarni); podrobneje se bomo s tem ukvarjali v poglavju Momenti funkcije gostote verjetnosti.
Nekaj primerov determinističnih signalov#
Spodja slika prikazuje periodične signale: najprej je prikazan trikotni signal, ki se ponavlja s periodo 1 s, nato je prikazan harmonski signal, ki se prav tako ponavlja s periodo 1 s.
Show code cell source
import numpy as np
import matplotlib.pyplot as plt
t, dt = np.linspace(0,4,1000, retstep=True)
plt.title('Periodični signali')
plt.plot(t, t%1, label='Periodični signal', alpha=0.8)
plt.plot(t, np.sin(2*np.pi*t+1), label='Harmonski signal', alpha=0.8)
plt.ylim(-2.1,2.1)
plt.xlabel('Čas [s]')
plt.grid()
plt.legend()
plt.show()
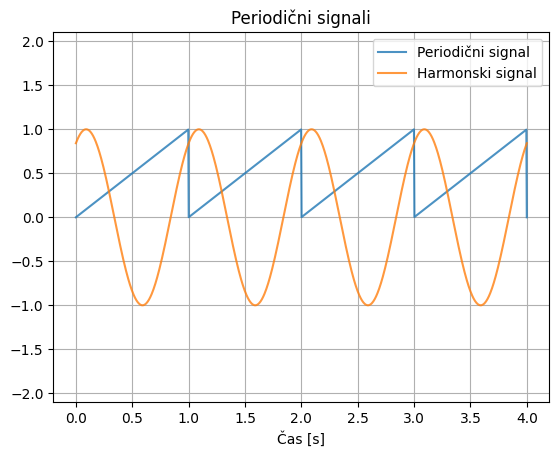
Zadnji signal predstavlja kompleksno periodični signal \(-\) ti signali so sestavljeni kot vsota več harmonskih komponent, perioda tega na sliki je 2 s.
Show code cell source
import numpy as np
import matplotlib.pyplot as plt
t, dt = np.linspace(0,10,1000, retstep=True)
plt.title('Deterministični signali')
plt.plot(t, np.sin(2*np.pi*t+1)+np.sin(3*np.pi*t+1), label='Kompleksno periodični signal', alpha=0.8)
plt.plot(t, np.sin(2*np.pi*t+1)+np.sin(3.075*np.pi*t+1), label='Skoraj periodični signal', alpha=0.8)
plt.ylim(-2.1,2.1)
plt.xlabel('Čas [s]')
plt.grid()
plt.legend(loc=8)
plt.show()
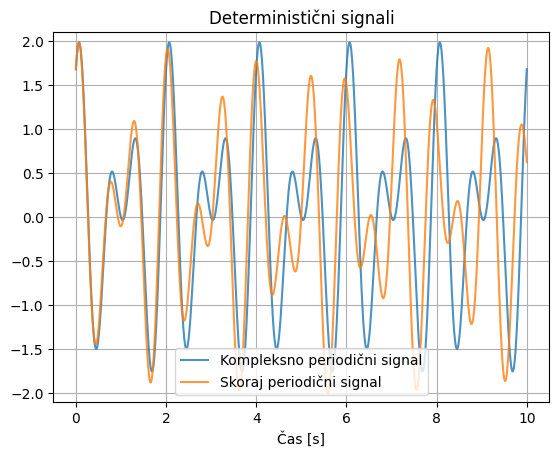
Pri neperiodičnih signalih bomo kot primer prikazali prehodni signal, ki nastane, ko dinamski sistem vzbudimo z impulzno motnjo.
Show code cell source
import numpy as np
import matplotlib.pyplot as plt
t, dt = np.linspace(0,4,1000, retstep=True)
omega = 10*np.pi
dušenje = 0.05
plt.title('Neperiodični signal')
plt.plot(t, np.exp(-omega*dušenje*t)*np.sin(omega*t+1), label='Prehodni pojav', alpha=0.8)
plt.ylim(-1.1,1.1)
plt.xlabel('Čas [s]')
plt.grid()
plt.legend()
plt.show()
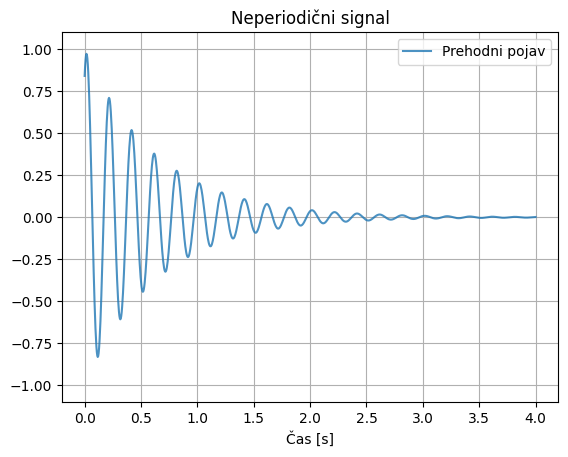
Kaotičnih neperiodičnih signalov tukaj ne bomo podrobneje obravnavali; zanje velja, da jih zaradi visoke stopnje dinamičnosti lahko zanesljivo napovedujemo samo za relativno kratek čas vnaprej, potem pa se njihovo obnašanje zdi čedalje bolj naključno.
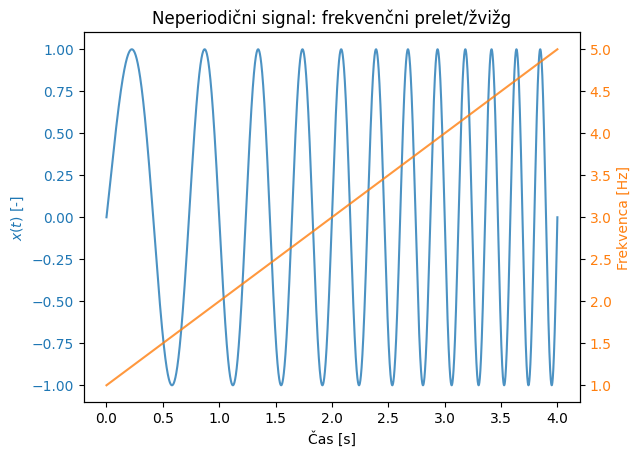
Pri vzbujanju dinamskih sistemov pogosto uporabimo frekvenčni prelet (ali tudi žvižg); spodaj je prikazan 4 s dolg linearni (frekvenca narašča monotono) žvižg od 1 do 5 Hz.
Show code cell source
import numpy as np
import matplotlib.pyplot as plt
import pyExSi as es
fs = 44000
T = 4
t = np.linspace(0,T,fs*T+1)
x, _, fr = es.sine_sweep(time=t, freq_start=1, freq_stop=5, mode='linear', freq_return=True)
fig, ax1 = plt.subplots()
plt.title('Neperiodični signal: frekvenčni prelet/žvižg')
ax1.set_xlabel('Čas [s]')
ax1.set_ylabel('$x(t)$ [-]', color='C0')
ax1.plot(t, x, color='C0', alpha=0.8)
ax1.tick_params(axis='y', labelcolor='C0')
ax2 = ax1.twinx()
ax2.set_ylabel('Frekvenca [Hz]', color='C1')
ax2.plot(t, fr, color='C1', alpha=0.8)
ax2.tick_params(axis='y', labelcolor='C1')
plt.show()
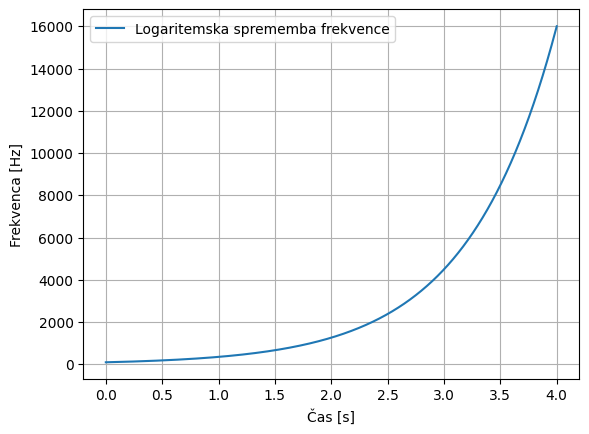
Pri analizi signalov nam občasno pomaga, da jih slišimo; spodaj lahko slišimo 4 s dolg logaritemski žvižg od 100 do 16000 Hz.
Show code cell source
import numpy as np
import pyExSi as es
from IPython.display import Audio, display
fs = 44000
T = 4
t = np.linspace(0,T,fs*T+1)
x, _, fr = es.sine_sweep(time=t, freq_start=100, freq_stop=16000, mode='logarithmic', freq_return=True)
display(Audio(data=x, rate=fs))
plt.plot(t, fr, label='Logaritemska sprememba frekvence')
plt.xlabel('Čas [s]')
plt.ylabel('Frekvenca [Hz]')
plt.grid()
plt.legend()
plt.show()
Nekaj primerov naključnih signalov#
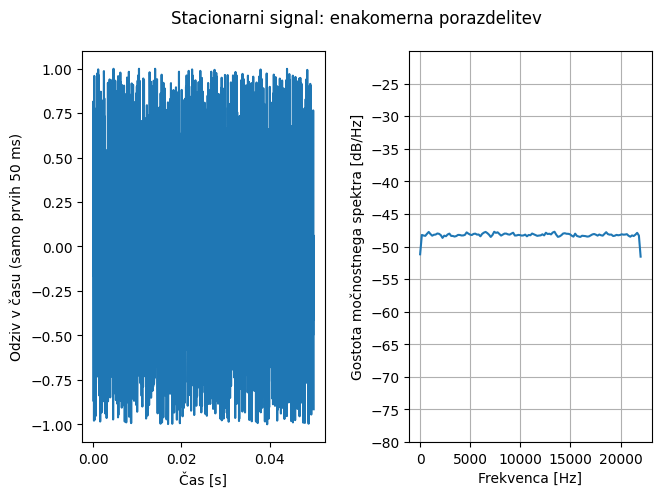
Spodnja slika prikazuje naključni signal z enakomerno porazdelitvijo. Na levi sliki je prikazanih prvih 50 ms podatkov v času, desna slika pa prikazuje gostoto močnostnega spektra (glejte Gostota močnostnega spektra (ang. Power Spectral Density, PSD)). Opazimo lahko, da ima enakomerna porazdelitev tudi v frekvenčni domeni relativno konstantno moč čez celotno analizirano frekvenčno področje (podatki so generirani s frekvenco vzorčenja 44 kHz).
Show code cell source
import numpy as np
import pyExSi as es
from IPython.display import Audio, display
fs = 44000
T = 4
t = np.linspace(0,T,fs*T+1)
N = len(t)
x = es.uniform_random(N=N)
sel = t<0.05
display(Audio(data=x, rate=fs))
fig, axs = plt.subplots(1,2)
fig.suptitle('Stacionarni signal: enakomerna porazdelitev')
plt.tight_layout(pad=1, w_pad=3)
axs[0].plot(t[sel], x[sel])
axs[0].set_xlabel('Čas [s]')
axs[0].set_ylabel('Odziv v času (samo prvih 50 ms)')
axs[1].psd(x, Fs=fs)
axs[1].set_xlabel('Frekvenca [Hz]')
axs[1].set_ylabel('Gostota močnostnega spektra [dB/Hz]')
axs[1].set_ylim(-80, -20)
axs[1].set_yticks(np.arange(-80,-20,5))
plt.show()
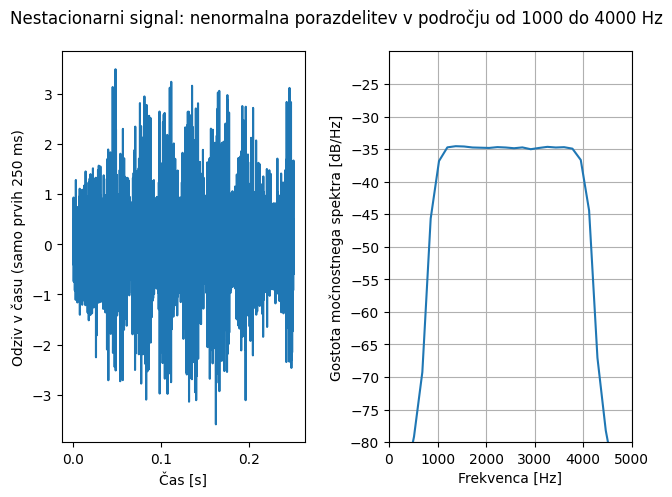
Ker je energija porazdeljena čez (pre)široko frekvenčno področje, je vzbujanje dinamskih sistemov z enakomerno porazdelitvijo redko primerno. Ponavadi uporabimo normalno (ali tudi Gaussovo) porazdelitev z definiranim frekvenčnim spektrom. Spodnja slika prikazuje normalno porazdelitev z enakomerno gostoto moči v frekvenčnem področju od 1000 do 4000 Hz.
Show code cell source
import numpy as np
import pyExSi as es
from IPython.display import Audio, display
fs = 44000
T = 4
t = np.linspace(0,T,fs*T+1)
N = len(t)
M = N // 2 + 1 # number of data points of frequency vector
freq = np.arange(0, M, 1) * fs / N # frequency vector
freq_lower = 1000 # PSD lower frequency limit [Hz]
freq_upper = 4000 # PSD upper frequency limit [Hz]
PSD = es.get_psd(freq, freq_lower, freq_upper) # one-sided flat-shaped PSD
x = es.random_gaussian(N, PSD, fs)
sel = t<0.05
display(Audio(data=x, rate=fs))
fig, axs = plt.subplots(1,2)
fig.suptitle(f'Stacionarni signal: normalna porazdelitev v področju od {freq_lower} do {freq_upper} Hz')
plt.tight_layout(pad=1, w_pad=3)
axs[0].plot(t[sel], x[sel])
axs[0].set_xlabel('Čas [s]')
axs[0].set_ylabel('Odziv v času (samo prvih 50 ms)')
axs[1].psd(x, Fs=fs)
axs[1].set_xlabel('Frekvenca [Hz]')
axs[1].set_ylabel('Gostota močnostnega spektra [dB/Hz]')
axs[1].set_xlim(0, 5000)
axs[1].set_ylim(-80, -20)
axs[1].set_yticks(np.arange(-80,-20,5))
plt.show()
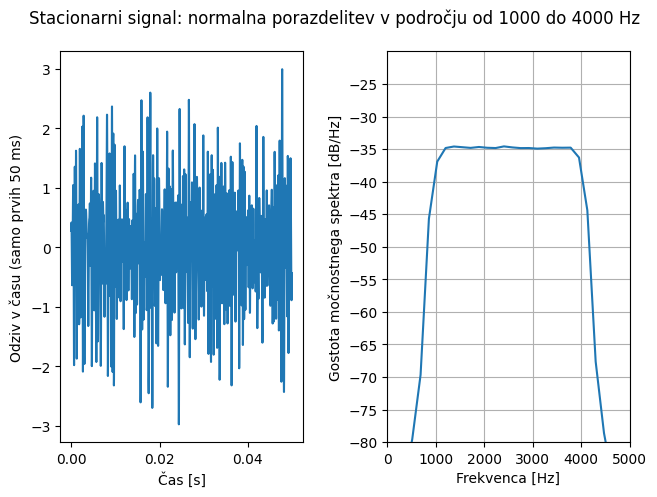
Za primerjavo si poglejmo še normalno porazdelitev z enakomerno gostoto moči v frekvenčnem področju od 100 do 400 Hz.
Show code cell source
import numpy as np
import pyExSi as es
from IPython.display import Audio, display
fs = 44000
T = 4
t = np.linspace(0,T,fs*T+1)
N = len(t)
M = N // 2 + 1 # number of data points of frequency vector
freq = np.arange(0, M, 1) * fs / N # frequency vector
freq_lower = 100 # PSD lower frequency limit [Hz]
freq_upper = 400 # PSD upper frequency limit [Hz]
PSD = es.get_psd(freq, freq_lower, freq_upper) # one-sided flat-shaped PSD
x = es.random_gaussian(N, PSD, fs)
sel = t<0.05
display(Audio(data=x, rate=fs))
fig, axs = plt.subplots(1,2)
fig.suptitle(f'Stacionarni signal: normalna porazdelitev v področju od {freq_lower} do {freq_upper} Hz')
plt.tight_layout(pad=1, w_pad=3)
axs[0].plot(t[sel], x[sel], label='Enakomerna porazdelitev')
axs[0].set_xlabel('Čas [s]')
axs[0].set_ylabel('Odziv v času (samo prvih 50 ms)')
axs[1].psd(x, Fs=fs)
axs[1].set_xlabel('Frekvenca [Hz]')
axs[1].set_ylabel('Gostota močnostnega spektra [dB/Hz]')
axs[1].set_xlim(0, 5000)
axs[1].set_ylim(-80, -20)
axs[1].set_yticks(np.arange(-80,-20,5))
plt.show()
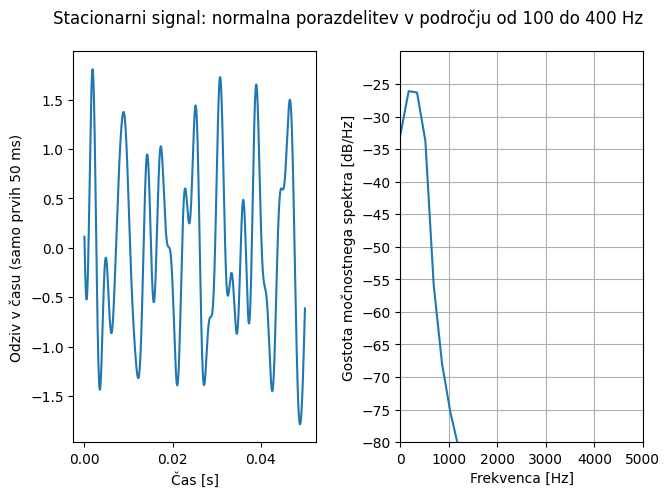
Poglejmo si še nestacionarni signal. Začnemo s pripravo stacionarnega signala enakomerne gostote moči v frekvenčnem področju od 1000 do 4000 Hz in nenormalno porazdelitvijo (s parametrom sploščenosti = 5, ang. kurtosis). Stacionarni signal nato moduliramo z nosilnim signalom v frekvenčnem področju od 10 do 20 Hz, da dobimo nestacionarni signal. Kljub temu da je gostota moči porazdeljena podobno kot zgoraj, se nenormalni in nestacionarni signal ponavadi sliši bistveno bolj neprijetno; v primeru vibracijskega utrujanja je nestacionarno obremenjevanje običajno tudi precej bolj škodljivo.
Show code cell source
import matplotlib.pyplot as plt
import numpy as np
import pyExSi as es
from IPython.display import Audio, display
fs = 44000
T = 4
t = np.linspace(0,T,fs*T+1)
N = len(t)
M = N // 2 + 1 # number of data points of frequency vector
freq = np.arange(0, M, 1) * fs / N # frequency vector
freq_lower = 1000 # PSD lower frequency limit [Hz]
freq_upper = 4000 # PSD upper frequency limit [Hz]
freq_lower_mod = 10 # modulating signals's PSD lower frequency limit [Hz]
freq_upper_mod = 20 # modulating signals's PSD upper frequency limit [Hz]
PSD = es.get_psd(freq, freq_lower, freq_upper) # one-sided flat-shaped PSD
PSD_modulating = es.get_psd(freq, freq_lower_mod, freq_upper_mod) # one-sided flat-shaped PSD
k_u = 5
x = es.nonstationary_signal(N,PSD,k_u=k_u, fs=fs, modulating_signal=('PSD',PSD_modulating))
sel = t<0.25
display(Audio(data=x, rate=fs))
fig, axs = plt.subplots(1,2)
fig.suptitle(f'Nestacionarni signal: nenormalna porazdelitev v področju od {freq_lower} do {freq_upper} Hz')
plt.tight_layout(pad=1, w_pad=3)
axs[0].plot(t[sel], x[sel])
axs[0].set_xlabel('Čas [s]')
axs[0].set_ylabel(f'Odziv v času (samo prvih 250 ms)')
axs[1].psd(x, Fs=fs)
axs[1].set_xlabel('Frekvenca [Hz]')
axs[1].set_ylabel('Gostota močnostnega spektra [dB/Hz]')
axs[1].set_xlim(0, 5000)
axs[1].set_ylim(-80, -20)
axs[1].set_yticks(np.arange(-80,-20,5))
plt.show()
