Programiranje in numerične metode v ekosistemu Pythona

Numerično reševanje diferencialnih enačb - robni problem

Kazalo

Reševanje dvotočkovnih robnih problemov

Pod dvotočkovnim robnim problemom razumemo navadno diferencialno enačbo drugega reda oblike:

$$\ddot y=f(t, y, \dot y),$$

ob predpisanih robnih pogojih:

$$y(a)=\alpha\qquad\textrm{in}\qquad y(b)=\beta.$$

Metode, ki smo jih spoznali pri reševanju začetnih problemov, tukaj neposredno niso uporabne, ker nimamo podanega odvoda v začetni točki pri $t=a$.

V nadaljevanju si bomo pogledali dva različna pristopa k reševanju robnih problemov:

  1. t. i. strelska metoda,
  2. metoda končnih razlik.

Strelska metoda

Rešujemo robni problem:

$$\ddot y=f(t, y, \dot y),\qquad y(a)=\alpha,\quad y(b)=\beta,$$

ki ga prevedemo na začetni problem tako, da si izberemo:

$$\dot y (a)=u.$$

Problem rešimo z numeričnimi metodami reševanja začetnega problema in rešitev označimo z $\theta(u, t)$.

Robni problem rešimo, ko izberemo $u$ tako, da velja:

$$r(u)=\theta(u,b)-\beta=0.$$

Dobili smo nelinearno enačbo, ki jo moramo rešiti; za izračun vrednosti mejnih preostankov $r(u)$ moramo numerično rešiti začetni problem.

Za rešitev enačbe $r(u)=0$ lahko uporabimo sekantno metodo. Izberemo $u_0$ in $u_1$ in na $i$-tem koraku izračunamo:

$$u_{i+1}=u_i-r(u_i)\,\frac{u_{i}-u_{i-1}}{r(u_{i})-r(u_{i-1})},\qquad i=2,3,\dots$$

Zaključimo, ko je: $$\left|r(u_{i+1})\right|<\epsilon.$$

Rešitev strelske metode je obremenjena z napako metode reševanja nelinearne enačbe $\epsilon$ in z napako numerične metode za reševanje začetnega problema.

Numerični zgled: poševni met

Na sliki je prikazan izstrelek mase $m$, ki ga izstrelimo s hitrostjo $\textbf{v}_0$.

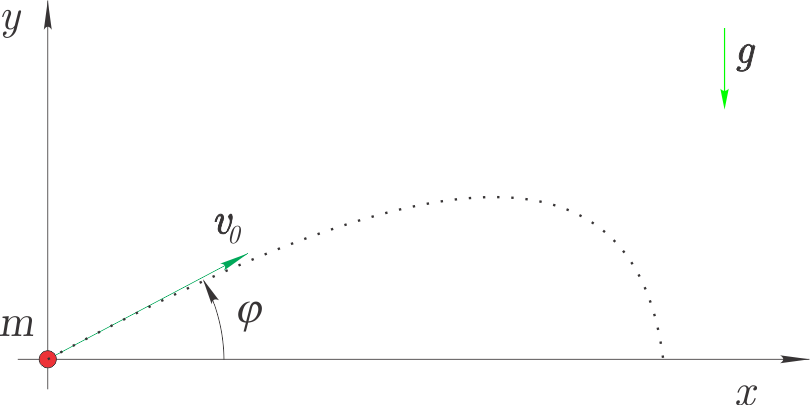
Velikost sile upora zraka je $|\textbf{F}|=c\,|\textbf{v}|^2$, potem sta gibalni enačbi:

$$x''(t)=-F_x/m\qquad\ddot y(t)=-F_y/m-g.$$

Komponente sile so (glejte izpeljavo pri poglavju iz reševanja začetnega problema sistema diferencialnih enačb): $$F_x=-c\,x'\,\sqrt{x'^2+y'^2},\qquad F_y=-c\,y'\,\sqrt{x'^2+y'^2}.$$

Vertikalni met

Najprej predpostavimo, da je $\varphi=90$° in torej v $x$ smeri nimamo gibanja. Zanima nas rešitev, ko izstrelek izstrelimo iz višine $y=0\,$m in mora pri času $t=b=1\,$s biti na višini $y(b)=10\,$m. Definirali smo robni problem:

$$y''(t)=F_y\,/m-g,\qquad y(0)=0,\quad y(1)=10.$$

Najprej moramo enačbo drugega reda:

$$y''=f(t, y, y') = F_y/m-g$$

preoblikovati na sistem dveh enačb prvega reda. Uporabimo $y_i=y^{i}$ ter upoštevamo $F_y=-c\,y'\,\sqrt{y'^2}$.

Odvajamo $y_i'=y_{i+1}$ in pripravimo sistem enačb prvega reda:

$$ \begin{array}{rcl} y'_0&=&y_1\\ y'_1&=&-c\,y'\,\sqrt{y'^2}/m-g \end{array} $$

Pripravimo seznam funkcij desnih strani:

In [69]:
def f_vert(t, y, g=9.81, m=1., c=0.5):
    return np.array([y[1], -g-c*y[1]*np.sqrt(y[1]**2)/m])

Uvozimo modula numpy in scipy.integrate.solve_ivp:

In [70]:
import numpy as np
from scipy.integrate import solve_ivp

ter pripravimo funkcijo za izračun mejnega preostanka pri času $b$ v odvisnosti od začetne hitrosti $v_0$ (privzeti zračni upor je $c=0.1$):

In [71]:
def r(v0=100., t=None, ciljna_lega=10., g=9.81, m=1., c=0.1):
    def f_vert_tmp(t, y): # pripravimo funkcijo z željenimi parametri
        return f_vert(t, y, g=g, m=m, c=c)
    sol = solve_ivp(f_vert_tmp, t_span=(t[0], t[-1]), y0=np.array([0., v0]))
    r = sol.y[0,-1] - ciljna_lega
    return r

Preverimo mejni preostanek pri začetnem pogoju $v_0=y'=50$ m/s:

In [72]:
t = np.linspace(0, 1, 100)
r(v0=50., t=t)
Out[72]:
$\displaystyle 5.63455093999735$

Opazimo, da je masa pri 1 sekundi 5,635 m nad ciljno višino.

Naš cilj je, da pri 1 sekundi masa doseže lego 10 m z natančnostjo 1e-6:

In [73]:
ciljna_lega = 10
epsilon = 1e-6

Izvedimo sedaj sekantno metodo:

In [74]:
x0 = 100
x1 = 50
for i in range(10):
    f0 = r(v0=x0, t=t, ciljna_lega=ciljna_lega)
    f1 = r(v0=x1, t=t, ciljna_lega=ciljna_lega)
    x2 = x1 - f1 * (x1 - x0)/(f1 - f0)
    err = r(v0=x2, t=t, ciljna_lega=ciljna_lega)
    print(f'Novi približek je {x2}, napaka je {err}.')
    x0 = x1
    x1 = x2
    if abs(err)<epsilon:
        rešitev = x2
        print(f'Rešitev {rešitev}')
        break

Novi približek je 5.644178759347113, napaka je -9.672536331804414.
Novi približek je 33.67258709458857, napaka je 2.2187017725280302.
Novi približek je 28.442965190719487, napaka je 0.8225839451367332.
Novi približek je 25.361704474139284, napaka je -0.10153714557803362.
Novi približek je 25.70025579721459, napaka je 0.004276366407131249.
Novi približek je 25.686573522825174, napaka je 2.16308919487318e-05.
Novi približek je 25.686503962731987, napaka je -4.623860405672531e-09.
Rešitev 25.686503962731987

Poglejmo si sedaj izračunano rešitev:

In [75]:
sol = solve_ivp(lambda t, y: f_vert(t, y, c=0.1),
                t_span=(t[0], t[-1]), y0=np.array([0., rešitev]),
                t_eval=t
               )

Zgoraj smo uporabili lambda izraz (dokumentacija). Izraz lambda t, y: f_vert(t, y, c=0.1) je ekvivalenten:

def ime_funkcije(t, y):
    return f_vert(t, y, c=0.1)

Uvozimo matplotlib:

In [76]:
import matplotlib.pyplot as plt
%matplotlib inline

Prikažemo rezultat:

In [77]:
plt.title('Vertikalni met')
plt.hlines(ciljna_lega,0., 1, 'C3', linestyles='dashed', label='Ciljna lega', alpha=0.5)
plt.plot(sol.t, sol.y[0], label='Lega $y$')
plt.xlabel('$t$ [s]')
plt.legend(loc=4)
plt.show()

Poševni met

Poglejmo si sedaj splošen poševni met (diferencialne enačbe so definirana že zgoraj). Najprej moramo sistem diferencialnih enačb drugega reda preoblikovati v sistem enačb prvega reda.

Uporabimo: $$y_0=x,~ y_1=x',~ y_2=y,~ y_3=y'$$

in dobimo sistem diferencialnih enačb prvega reda:

$$ \begin{array}{rcl} y_0'&=&y_1\\ y_1'&=&F_x/m\\ y_2'&=&y_3\\ y_3'&=&F_y/m-g.\\ \end{array} $$

Pripravimo seznam funkcij desnih strani:

In [78]:
def f_poševno(t, y, g=9.81, m=1., c=0.1):
    x, vx, yy, vy = y
    return np.array([vx, -c*vx*np.sqrt(vx**2+vy**2)/m, vy, -g-c*vy*np.sqrt(vx**2+vy**2)/m])

Pripravimo še funkcijo za izračun mejnega preostanka pri času $b=1$ v odvisnosti od vektorja začetne hitrosti $\mathbf{v}_0$:

In [79]:
def r_poševno(v0=[5., 100.], t=None, ciljna_lega=np.array([10, 5.]), g=9.81, m=1., c=0.1):
    sol = solve_ivp(lambda t, y: f_poševno(t, y, g=g, m=m, c=c),
                      t_span=(t[0], t[-1]),
                      y0=[0, v0[0], 0, v0[1]])
    r = sol.y[0:3:2, -1] - ciljna_lega
    return r

Preverimo mejni preostanek pri začetnem pogoju $\mathbf{v}_0=[100., 100.]\,$m/s:

In [80]:
r_poševno(v0=[100., 100.],t=t)
Out[80]:
array([ 9.66195325, 11.84726075])

Za iskanje korena sistema nelinearnih funkcij smo že spoznali funkcijo scipy.optimize.root (dokumentacija):

root(fun, x0, args=(), method='hybr', jac=None,
     tol=None, callback=None, options=None)

Najprej jo uvozimo:

In [81]:
from scipy import optimize

Potem uporabimo z začetnim ugibanjem $\mathbf{v}_0$:

In [82]:
rešitev = optimize.root(r_poševno, np.array([100., 100.]), args=(t))

Rešitev je:

In [83]:
rešitev
Out[83]:
    fjac: array([[-0.93392958,  0.35745704],
       [-0.35745704, -0.93392958]])
     fun: array([ 1.01252340e-13, -3.44613227e-13])
 message: 'The solution converged.'
    nfev: 17
     qtf: array([ 1.06701116e-09, -1.31136287e-09])
       r: array([-0.40775374,  0.24087448, -0.37544067])
  status: 1
 success: True
       x: array([19.37894314, 16.55482478])

Atribut rešitev.x vsebuje vektor izračunanih rešitev ([19.37894314, 16.55482478]). Preverimo mejni preostanek pri izračunani rešitvi:

In [84]:
r_poševno(v0=rešitev.x, t=t)
Out[84]:
array([ 1.01252340e-13, -3.44613227e-13])

Poglejmo si sedaj izračunano rešitev:

In [85]:
sol = solve_ivp(lambda t, y: f_poševno(t, y, g=9.81, m=1., c=.1),
                t_span=(t[0], t[-1]),
                y0=[0, rešitev.x[0], 0, rešitev.x[1]],
                t_eval=t)

Prikažemo rezultat:

In [86]:
plt.title('Poševni met')
plt.hlines(10,0., 1, 'C3', linestyles='dashed', label='Ciljna lega za $x$', alpha=0.5)
plt.hlines(5,0., 1, 'C4', linestyles='dashed', label='Ciljna lega za $y$', alpha=0.5)
plt.plot(sol.t, sol.y[0], label='Lega $x$', color='C3')
plt.plot(sol.t, sol.y[2], label='Lega $y$', color='C4')
plt.xlabel('$t$ [s]')
plt.legend()
plt.show()

Uporaba scipy.integrate.solve_bvp

Namesto scipy.integrate.solve_ivp in scipy.optimize lahko uporabimo vgrajeno funkcijo za reševanje robnih problemov scipy.integrate.solve_bvp (BVP - angl. Boundary Value Problem):

scipy.integrate.solve_bvp(fun, bc, x, y, 
                          p=None, S=None, fun_jac=None, bc_jac=None, 
                          tol=0.001, max_nodes=1000, verbose=0)

Pojasnilo vseh argumentov je v dokumentaciji, tukaj bomo izpostavili nekatere:

  • fun je desna stran (func(t, y...)),
  • bc je mejni preostanek: bc(y(a), y(b)) = 0
  • x numerično polje (dimenzija (m)) neodvisne spremenljivke x[0]=a in x[-1]=b,
  • y numerično polje (dimenzija (n, m)) začetnih vrednosti.

Rezultat klicanja solve_bvp je objekt z atributi (izbrani):

  • x vrednosti neodvisne spremenljivke pri katerih je izračunan rezultat,
  • y rezultat,
  • sol rezultat v obliki kubičnega zlepka,
  • success je True, če je bila rešitev konvergirala.

Poglejmo primer:

In [87]:
from scipy.integrate import solve_bvp

Definirajmo neodvisno spremenljivko

In [88]:
t = np.linspace(0, 1, 15)

In mejni preostanek (želimo, da je pri času b lega $x=10$ m in $y=5$ m):

In [89]:
def mejni_preostanek(ya, yb):
    return np.array([ya[0], ya[2], yb[0]-10, yb[2]-5])

Definirajmo še začetne vrednosti hitrosti (kot začetno ugibanje):

In [90]:
y0 = np.zeros((4, t.size))
y0[1] = 5   # hitrost v x smeri
y0[3] = 100 # hitrost v y smeri

In rešimo robni problem in opis rezultata

In [91]:
sol = solve_bvp(lambda t, y: f_poševno(t, y, g=9.81, m=1., c=.1), 
                bc=mejni_preostanek, x=t, y=y0)
In [92]:
sol.message
Out[92]:
'The algorithm converged to the desired accuracy.'

Prikažimo rezultat:

In [93]:
plt.title('Poševni met')
plt.hlines(10,0., 1, 'C3', linestyles='dashed', label='Ciljna lega za $x$', alpha=0.5)
plt.hlines(5,0., 1, 'C4', linestyles='dashed', label='Ciljna lega za $y$', alpha=0.5)
plt.plot(sol.x, sol.y[0], label='Lega $x$', color='C3')
plt.plot(sol.x, sol.y[2], label='Lega $y$', color='C4')
plt.xlabel('$t$ [s]')
plt.legend()
plt.show()

Numerični zgled: nosilec z obremenitvijo

Poglejmo si nosilec:

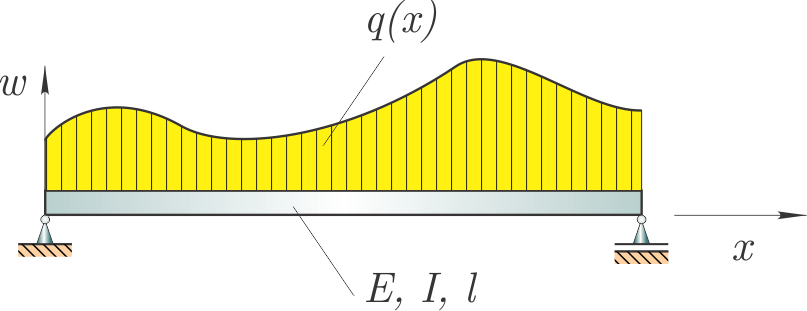
Poves $w(x)$ nosilca popiše diferencialna enačba četrtega reda:

$$-E\,I\frac{\textrm{d}^4}{\textrm{d}x^4}w(x)+q(x)=0.$$

Znane konstante so $E,I,l$ in je $q(x)$ porazdeljena obremenitev.

Robni pogoji (členkasto vpet nosilec): $$w(0)=w(l)=0\quad\textrm{in}\quad w''(0)=w''(l)=0$$

Parametri so:

  • $I=2.1\cdot10^{-5}\,$m$^4$,
  • $E=2.1\cdot10^{11}\,N/$m$^2$,
  • $l=10\,$m.

Porazdeljena obremenitev $q(x)$ bo definirana pozneje.

Najprej moramo diferencialno enačbo četrtega reda preoblikovati v sistem diferencialnih enačb prvega reda. Uporabimo: $$y_0=w,~ y_1=w',~ y_2=w'',~ y_3=w'''$$

in dobimo sistem diferencialnih enačb prvega reda:

$$ \begin{array}{rcl} y_0'&=&y_1\\ y_1'&=&y_2\\ y_2'&=&y_3\\ y_3'&=&q(x)/(EI).\\ \end{array} $$

Pripravimo različne porazdeljene obremenitve:

In [94]:
def q_konstanta(x, F_0=1e3, l=10):
    return -F_0*np.ones_like(x)

def q_trikotna(x, F_0=1e3, l=10):
    return -F_0*x/l

def q_pol_sinusna(x, F_0=1e3, l=10):
    return -F_0*np.sin(np.pi*x/l)

Definirajmo dolžino (ostale parametre, $I, E$, bomo uporabili privzete):

In [95]:
l = 10.
In [96]:
x = np.linspace(0, l, 15)
plt.fill_between(x, q_konstanta(x), alpha=0.4, label='Konstantna')
plt.fill_between(x, q_pol_sinusna(x), alpha=0.4, label='Pol-sinusna')
plt.fill_between(x, q_trikotna(x), alpha=0.4, label='Trikotna')
plt.title('Porazdeljena obremenitev $q(x)$')
plt.legend()
plt.show()

Pripravimo seznam funkcij desne strani:

In [97]:
def f_nosilec_konstanta(x, y, E=2.1e11, I=2.1e-5):
    return np.array([y[1], y[2], y[3], q_konstanta(x)/(E*I)], dtype=float)
def f_nosilec_pol_sinusna(x, y, E=2.1e11, I=2.1e-5):
    return np.array([y[1], y[2], y[3], q_pol_sinusna(x)/(E*I)])
def f_nosilec_trikotna(x, y, E=2.1e11, I=2.1e-5):
    return np.array([y[1], y[2], y[3], q_trikotna(x)/(E*I)])

Definirajmo sedaj robne pogoje oz. mejni preostanek (poves in moment sta na robovih enaka nič):

In [98]:
def mejni_nosilec(ya, yb):
    return np.array([ya[0], ya[2], yb[0], yb[2]])

Definirajmo še začetne vrednosti hitrosti (kot začetno ugibanje):

In [99]:
y0 = np.zeros((4, x.size), dtype=float)
y0[1] = 1. # w'
y0[3] = 1. # w'''

In rešimo robni problem (za vse tri tipe obremenitve):

In [100]:
sol_ko = solve_bvp(f_nosilec_konstanta, bc=mejni_nosilec, x=x, y=y0)
sol_pol_sin = solve_bvp(f_nosilec_pol_sinusna, bc=mejni_nosilec, x=x, y=y0)
sol_trikotna = solve_bvp(f_nosilec_trikotna, bc=mejni_nosilec, x=x, y=y0)

Rezultat prikažimo za konstantno obremenitev:

In [101]:
plt.fill_between(sol_ko.x, sol_ko.y[0], label='Poves $w$', alpha=0.5)
plt.fill_between(sol_ko.x, sol_ko.y[1], label='Naklon $w\'$', alpha=0.5)
plt.title('Konstantna obremenitev')
plt.legend()
plt.show()

In primerjavo povesa za različne tipe obremenitve:

In [102]:
plt.fill_between(sol_ko.x, sol_ko.y[0], label='Konstantna $w$', alpha=0.5)
plt.fill_between(sol_pol_sin.x, sol_pol_sin.y[0], label='Pol-sinusna $w$', alpha=0.5)
plt.fill_between(sol_trikotna.x, sol_trikotna.y[0], label='Trikotna $w$', alpha=0.5)
plt.title('Poves pri različnem tipu obremenitve')
plt.legend()
plt.show()

Metoda končnih razlik

Rešujemo robni problem:

$$y''=f(t, y, y'),\qquad y(a)=\alpha,\quad y(b)=\beta.$$

Velja torej: $$a=t_0,\quad b=t_{n-1}.$$

Pri metodi končnih razlik za reševanje robnega problema uporabimo diferenčno shemo. Predpostavimo, da imamo interval $[a,b]$, na katerem rešujemo diferencialno enačbo (neodvisna spremenljivka) razdeljeno na enake podintervale (točk je $n$):

$$t=[t_0, t_1,\dots, t_{n-1}].$$

Odvode nadomestimo s centralno diferenčno shemo:

Odvod$\downarrow$ $\backslash$ Vrednosti $\rightarrow$ $y_{i-2}$ $y_{i-1}$ $y_{i}$ $y_{i+1}$ $y_{i+2}$
$y_i'=\frac{1}{h}\cdot$ 0 -0.5 0 0.5 0
$y_i''=\frac{1}{h^2}\cdot$ 0 1 -2 1 0
$y_i'''=\frac{1}{h^3}\cdot$ -0.5 1 0 -1 0.5
$y_i^{(4)}=\frac{1}{h^4}\cdot$ 1 -4 6 -4 1

Prikazana centralna diferenčna shema ima napako drugega reda $\mathcal{O}(h^{2})$.

V $i$-ti točki navadno differencialno enačbo drugega reda s centralimi diferencami zapišemo:

$$\frac{1}{h^2}\left(y_{i-1}-2\,y_{i}+y_{i+1}\right)+\mathcal{O}(h^{2})=f\left(t_i, y_i, \frac{1}{2h}\left(-y_{i-1}+y_{i+1}\right)+\mathcal{O}(h^{2})\right).$$

Če zanemarimo napako metode:

$$\frac{1}{h^2}\left(y_{i-1}-2\,y_{i}+y_{i+1}\right)=f\left(t_i, y_i, \frac{1}{2h}\left(-y_{i-1}+y_{i+1}\right)\right),\qquad i=1,2,\dots,n-2.$$

Zgornjo enačbo lahko zapišemo za $n-2$ notranjih točk, kar pomeni, da nam do rešljivega sistema enačb za $n$ neznank manjkata še dve enačbi. Ti dve enačbi sta robna pogoja:

$$y_0=\alpha,\quad y_{n-1}=\beta.$$

V primeru linearnega robnega problema moramo za izračun $n$ neznank $y_i$ rešiti sistem $n$ linearnih enačb (če je pa nelinearen, pa sistem nelinearnih enačb).

Ocena napake

Točen rezultat $y(t_{i})$ pri velikosti koraka $h$ je: $$y(t_{i})=y_{i,h}+E_{i,h},$$ kjer je $y_{i,h}$ numerični približek in $E_h$ napaka metode. Ker je globalna napaka drugega reda, lahko napako zapišemo: $$E_{i,h}=k\,h^2,$$

Podobno lahko za velikost koraka $2h$ zapišemo: $$y(t_{j})=y_{j,2h}+E_{j,2h},$$ kjer je $y_{j,2h}$ numerični približek in $E_{2h}$ napaka metode in je: $$E_{j,2h}=k\,(2\,h)^2=4\,k\,h^2$$

Ob predpostavki, da je konstanta $k$ pri koraku $h$ in koraku $2h$ enaka, lahko določimo oceno napake pri boljšem približku $E_h$. Najprej izenačimo točna rezultat $y(t_{i})$ pri koraku $h$ in rezultat $y(t_{j})$ pri koraku $2h$ (velja $i=2\,j$, $j=1,2,\dots$):

$$y_{i,h}+k\,h^2=y_{j,2h}+4\,k\,h^2$$

sledi:

$$3\,k\,h^2=y_{2j,h}-y_{j,2h}$$

in nato izračunamo oceno napake:

$$E_{j,h}=\frac{y_{2j,h}-y_{j,2h}}{3}.$$

Numerični zgled: vertikalni met

Zgoraj smo vertikalni met rešili s strelsko metodo; uporabimo sedaj metodo končnih razlik. Najprej robni problem: $$y''(t)=F_y/m-g,\qquad y(0)=0,\quad y(1)=10.$$ zapisati s pomočjo centralne diferenčne sheme ($F_y=-c\,y'$):

$$\frac{1}{h^2}\left(y_{i-1}-2\,y_{i}+y_{i+1}\right)= -c\left(\frac{1}{2h}\left(-y_{i-1}+y_{i+1}\right)\right)/m-g.$$

(Tukaj smo predpostavili, da je zračni upor linearno odvisen od hitrost. V nasprotnem primeru bi imeli nelinearni robni problem, in posledično razvili sistem nelinearnih enačb.)

Zgornji izraz preoblikujemo: $$(2-c\,h/m)\,y_{i-1}-4\,y_{i}+(2+c\,h/m)\,y_{i+1}=-2\,g\,h^2,\qquad i=1,2,\dots,n-2.$$

Robna pogoja sta:

$$y_0=0,\qquad y_{n-1}=10$$

Robni problem smo torej preoblikovali na sistem $n$ linearnih enačb. Poglejmo si sedaj konkreten izračun za $n=11$; najprej definirajmo konstante, časovni vektor t in korak h:

In [103]:
n = 11 # liho število
c = 0.5
m = 1.0
g = 9.81
t = np.linspace(0, 1, n)
h = t[1]

Nato nadaljujemo z izračunom tridiagonalne matrike koeficientov A.

Pomagamo si s funkcijo numpy.diag() (dokumentacija):

numpy.diag(v, k=0)

s parametroma:

  • v vektor, ki bo prirejen diagonali,
  • k diagonala, kateri se priredi v. k=0 uporabimo za glavno diagonalo, k<0 oz. k>0 uporabimo za diagonale pod oz. nad glavno diagonalo.
In [104]:
A = np.diag(-4*np.ones(n), 0) + \
    (2-c*h/m)*np.diag(np.ones(n-1), -1) + \
    (2+c*h/m)*np.diag(np.ones(n-1), 1)
A[:4,:4]
Out[104]:
array([[-4.  ,  2.05,  0.  ,  0.  ],
       [ 1.95, -4.  ,  2.05,  0.  ],
       [ 0.  ,  1.95, -4.  ,  2.05],
       [ 0.  ,  0.  ,  1.95, -4.  ]])

Definirajmo še vektor konstant:

In [105]:
b = -2*g*h**2 * np.ones(n)

Sedaj popravimo matriko koeficientov A in vektor konstant b, da zadostimo robnim pogojem:

$$y_0=0,\quad y_{n-1}=10.$$
In [106]:
A[0,0] = 1
A[0,1] = 0
A[-1,-2] = 0
A[-1,-1] = 1
In [107]:
b[0] = 0.
b[-1] = 10.

Rešimo sistem linearnih enačb:

In [108]:
y_mkr = np.linalg.solve(A, b)

Prikažemo rezultat:

In [109]:
plt.title('Vertikalni met (upor zraka: $-c\,\dot y$)')
plt.hlines(10, 0, 1, 'C3', label='Ciljna lega', linestyles='dashed', alpha=0.5)
plt.plot(t, y_mkr, '.', label='Metoda končnih razlik')
plt.xlabel('$t$ [s]')
plt.ylabel('$y$ [m]')
plt.legend()
plt.show()

S pomočjo funkcije numpy.gradient() izračunamo še hitrost in pospešek:

In [110]:
v_mkr = np.gradient(y_mkr,h, edge_order=2)
a_mkr = np.gradient(v_mkr,h, edge_order=2)
v_mkr[:4]
Out[110]:
array([17.99109496, 16.20009044, 14.45276895, 12.79068266])

Izračunajmo sedaj še rezultat z dvojnim korakom:

In [111]:
n2h = n//2+1
t2h = np.linspace(0, 1, n2h)
h2h = t[1]
A2h = np.diag(-4*np.ones(n2h), 0) + \
    (2-c*h2h/(m))*np.diag(np.ones(n2h-1), -1) + \
    (2+c*h2h/(m))*np.diag(np.ones(n2h-1), 1)
b2h = -2*g*h2h**2 * np.ones(n2h)
A2h[0,0] = 1
A2h[0,1] = 0
A2h[-1,-1] = 1
A2h[-1,-2] = 0
b2h[0] = 0.
b2h[-1] = 10.
y2h_mkr = np.linalg.solve(A2h, b2h)

Primerjajmo prvih šest rezultatov pri koraku $2h$:

In [112]:
y2h_mkr[:6]
Out[112]:
array([ 0.        ,  2.40584652,  4.59862736,  6.58873597,  8.38605878,
       10.        ])

z vsakim drugim rezultatom pri koraku $h$:

In [113]:
y_mkr[:12:2]
Out[113]:
array([ 0.        ,  3.24001809,  5.79815462,  7.73931207,  9.12221538,
       10.        ])

Sedaj lahko ocenimo napako:

In [114]:
(y_mkr[::2]-y2h_mkr)/3
Out[114]:
array([0.        , 0.27805719, 0.39984242, 0.38352537, 0.24538553,
       0.        ])

Numerični zgled: nosilec z obremenitvijo

Vrnimo se k robnemu problemu nosilca s polsinusno obremenitvijo ($q(x)=-F_0\,\sin(\pi\,x/l))$), ki smo ga že obravnavali s strelsko metodo.

Diferencialno enačbo četrtega reda zapišemo s pomočjo centralne diferenčne sheme (za $i$-to točko):

$$-\frac{E\,I}{h^4}\left(1\,w_{i-2} - 4\,w_{i-1} + 6\,w_{i} - 4\,w_{i+1} + 1\, w_{i+2}\right) - F_0\,\sin(\pi\,x_i/l)= 0.$$

Robni pogoji so štirje, najprej poves na robovih:

$$w_0=w_{n-1}=0$$

Ker na robovih ni momenta, je drugi odvod nič. S centralno diferenčno shemo torej zapišemo dodatne enačbe:

$$w_{-1}-2\,w_{0}+w_{1}=0\qquad w_{n-2}-2\,w_{n-1}+w_{n}=0.$$

Če za neodvisno spremenljivko $x$ uporabimo $n$ ekvidistantnih točk, potem diferencialno enačbo četrtega reda zapišemo za $n-2$ notranje točke. S tem pridobimo dodatni nefizikalni točki $w_{-1}$ in $w_n$. Če dodamo še štiri robne pogoje, imamo rešljiv sistem linearnih enačb z $n+2$ neznakami in $n+2$ enačbami.

Najprej pripravimo podatke, neodvisno spremenljivko x in korak h:

In [115]:
l = 10.
E = 2.1e11
I = 2.1e-5
F_0= 1e3
n = 100
x = np.linspace(0, l, n)
h = x[1]

Nato pripravimo matriko koeficientov (matrika je dimenzije (n+2, n+2), v prvi in v zadnji dve vrstici bi lahko zapisali tudi vrednosti 0, to bomo pozneje popravili):

In [116]:
A = +1*np.diag(np.ones(n-2+2), -2) \
    -4*np.diag(np.ones(n-1+2), -1) \
    +6*np.diag(np.ones(n+2), 0)  \
    -4*np.diag(np.ones(n-1+2), +1)  \
    +1*np.diag(np.ones(n-2+2), +2)
A[:4,:4]
Out[116]:
array([[ 6., -4.,  1.,  0.],
       [-4.,  6., -4.,  1.],
       [ 1., -4.,  6., -4.],
       [ 0.,  1., -4.,  6.]])

Definirajmo še vektor konstant (dodamo en element na koncu in en na začetku):

In [117]:
b = np.zeros(n+2)
b[2:-2] = - h**4 * F_0*np.sin(np.pi*x[1:-1]/l)/(E*I)
b[:4]
Out[117]:
array([ 0.00000000e+00,  0.00000000e+00, -7.48966545e-10, -1.49717894e-09])

Sedaj popravimo matriko koeficientov A in vektor konstant b, da zadostimo robnim pogojem.

Najprej $w_0=w_{n-1}=0$:

In [118]:
A[0,:3]= np.array([0, 1, 0])
b[0] = 0
A[-1,-3:]= np.array([0, 1, 0])
b[-1] = 0

Nato $w_{-1}-2\,w_{0}+w_{1}=0$ in $w_{n-2}-2\,w_{n-1}+w_{n}=0$:

In [119]:
A[1,:4] = np.array([1, -2, 1,0])
b[1] = 0
A[-2,-4:] = np.array([0, 1, -2, 1])
b[-2] = 0
In [120]:
A[:5,:5]
Out[120]:
array([[ 0.,  1.,  0.,  0.,  0.],
       [ 1., -2.,  1.,  0.,  0.],
       [ 1., -4.,  6., -4.,  1.],
       [ 0.,  1., -4.,  6., -4.],
       [ 0.,  0.,  1., -4.,  6.]])
In [121]:
A[-5:,-5:]
Out[121]:
array([[ 6., -4.,  1.,  0.,  0.],
       [-4.,  6., -4.,  1.,  0.],
       [ 1., -4.,  6., -4.,  1.],
       [ 0.,  0.,  1., -2.,  1.],
       [ 0.,  0.,  0.,  1.,  0.]])
In [122]:
b[:5]
Out[122]:
array([ 0.00000000e+00,  0.00000000e+00, -7.48966545e-10, -1.49717894e-09,
       -2.24388381e-09])
In [123]:
b[-5:]
Out[123]:
array([-2.24388381e-09, -1.49717894e-09, -7.48966545e-10,  0.00000000e+00,
        0.00000000e+00])

Rešimo sistem linearnih enačb:

In [124]:
y_mkr = np.linalg.solve(A, b)

Prikažemo rezultat:

In [125]:
plt.title('Poves ob polsinusni obremenitvi')
plt.plot(sol_pol_sin.x, sol_pol_sin.y[0], 'o', label='Strelska metoda')
plt.plot(x, y_mkr[1:-1], '.', label='Metoda končnih razlik')
plt.xlabel('$x$ [m]')
plt.ylabel('$w$ [m]')
plt.legend()
plt.show()

Dodatno: simbolna rešitev nosilca

Tukaj si bomo pogledali simbolno reševanje robnega problema. Poudariti je treba, da gre tukaj zgolj za zgled, ki ga lahko naredimo za obravnavani nosilec z relativno enostavno polsinusno obremenitvijo. V praksi so seveda obremenitve in tudi oblike nosilca lahko bistveno bolj zahtevne in takrat druge poti kot numeričnega reševanja skoraj nimamo na voljo.

Najprej uvozimo sympy:

In [126]:
import sympy as sym
sym.init_printing()

Definirajmo spremenljivke:

In [136]:
w = sym.Function('w')
x, E, I, F_0, l = sym.symbols('x, E, I, F_0, l')

Definirajmo differencialno enačbo (robne pogoje dodamo pozneje):

In [137]:
eq = sym.Eq(-E*I*w(x).diff(x,4)-F_0*sym.sin(sym.pi*x/l),0)
eq
Out[137]:
$\displaystyle - E I \frac{d^{4}}{d x^{4}} w{\left(x \right)} - F_{0} \sin{\left(\frac{\pi x}{l} \right)} = 0$

Rešimo:

In [156]:
sol = sym.dsolve(eq, func=w(x), hint='nth_linear_constant_coeff_undetermined_coefficients',
                 ics={
                     w(0):0,                      #poves pri x=0 je nič
                     w(x).diff(x,2).subs(x, 0): 0,#moment pri x=0 je nič
                     w(x).subs(x, l): 0,                     #poves pri x=l je nič
                     w(x).diff(x, 2).subs(x, l): 0 #moment pri x=l je nič                 
                 })
sol
Out[156]:
$\displaystyle w{\left(x \right)} = - \frac{F_{0} l^{4} \sin{\left(\frac{\pi x}{l} \right)}}{\pi^{4} E I}$
In [159]:
podatki = {E: 2.1e11, I: 2.1e-5, l: 10, F_0:1e3}
resitev_np = sym.lambdify(x, sol.rhs.subs(podatki), modules='numpy')
x_ana = np.linspace(0, podatki[l], 100)
y_ana = resitev_np(x_ana)
In [160]:
plt.title('Upogib ob polsinusni obremenitvi')
plt.plot(x_ana, y_ana, '-', label='Analitična rešitev')
plt.xlabel('$x$ [m]')
plt.ylabel('$w$ [m]')
plt.legend()
plt.show()

Primerjajmo sedaj analitično rešitev, z rešitivijo z metodo končnih razlik in strelsko metodo:

In [161]:
[np.min(y_ana), np.min(y_mkr), np.min(sol_pol_sin.y[0])]
Out[161]:
$\displaystyle \left[ -0.02327594116013143, \ -0.023279847998899324, \ -0.02327864621402198\right]$